BZOJ4237: 稻草人
n<=200000个平面上的点，问有多少对点(i,j)满足Xi<Xj，Yi<Yj，且不存在k使得Xi<Xk<Xj && Yi<Yk<Yj。保证Xi，Yi互不相同。
看起来像一个偏序问题，先按Xi排序然后分治来做，但是那坨长长的东西怎么搞呢？试了若干种方法，不会，看题解。
首先Y这一维是要满足的，所以分治时把左右两边按Y归并排序后来看左边对右边的贡献。但是有诸多情况。。。
实验+总结一下可以观察到下面两个性质：
（1）
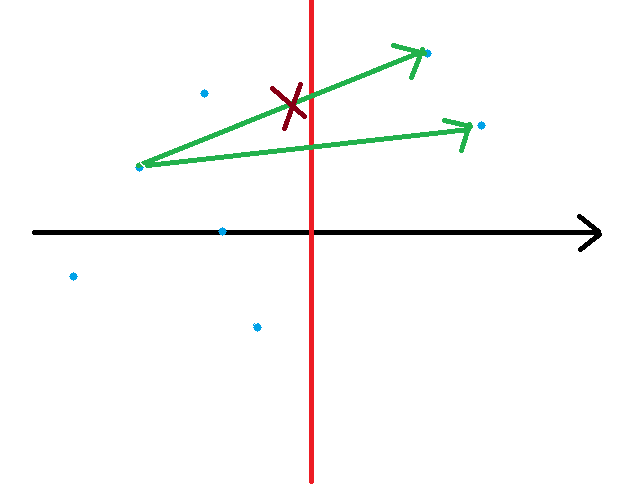
两边按y排序（从大到小）后，开两个指针扫一扫可以满足条件Yi<Yj，然而并不是所有的都满足，如上图，存在一些遮拦的点。
由于y是从大到小排序的，可以看一下在左半边把点按y从大到小加进去后会发生什么遮拦情况：
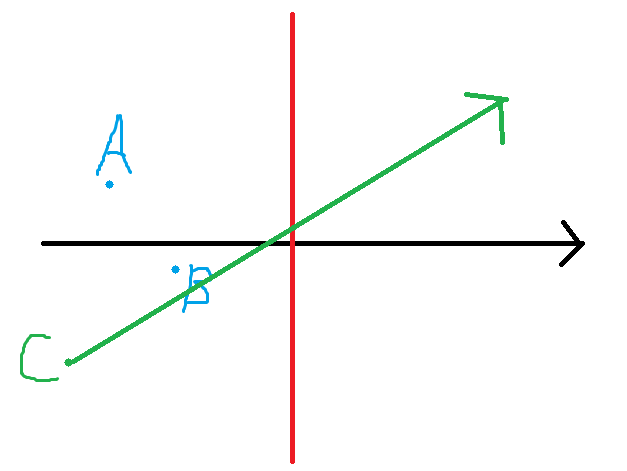
如图，y从大到小将点加入后，左边若是Yi>Yj却Xi<Xj，那么能被i点（A）拦到的点一定能被j点（B）拦到，因此左半边维护一个Xi随Yi减小而减小的栈，即可找到左边点的互相遮拦限制。如上图中，C点需要在右边找到比B点的y小而比C点的y大的来计算答案。
（2）看右边点的互相遮拦：
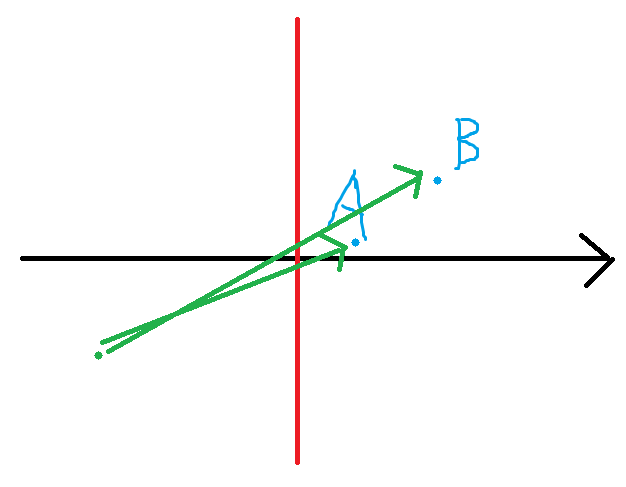
由于y是从大到小加进去的，新加进的左边的C点的y一定比原来加进的A和B点要小，此时B被A完全拦住。因此右边若Yi>Yj，则必须Xi<Xj，右边维护一个栈即可满足条件3.
两个栈就完了吗？嗯。
1 #include<stdio.h> 2 #include<string.h> 3 #include<algorithm> 4 #include<stdlib.h> 5 //#include<iostream> 6 using namespace std; 7 8 int n; 9 #define maxn 200011 10 struct Point 11 { 12 int x,y; 13 bool operator < (const Point &b) const {return x<b.x;} 14 }a[maxn]; 15 16 int ord[maxn],tmpord[maxn]; 17 int stal[maxn],topl,star[maxn],topr; 18 #define LL long long 19 LL ans=0; 20 void solve(int L,int R) 21 { 22 if (L==R) {ord[L]=L;return;} 23 const int mid=(L+R)>>1; 24 solve(L,mid);solve(mid+1,R); 25 topl=topr=0; 26 for (int i=L,j=mid+1;i<=mid;i++) 27 { 28 while (j<=R && a[ord[j]].y>a[ord[i]].y) 29 { 30 while (topr && a[star[topr]].x>a[ord[j]].x) topr--; 31 star[++topr]=ord[j++]; 32 } 33 while (topl && a[stal[topl]].x<a[ord[i]].x) topl--; 34 stal[++topl]=ord[i]; 35 int l=0,r=topr; 36 while (l<r) 37 { 38 const int mid=(l+r+1)>>1; 39 if (a[star[mid]].y>a[ord[i]].y) l=mid; 40 else r=mid-1; 41 } 42 int up=l,down; 43 if (topl==1) down=1; 44 else 45 { 46 l=1,r=topr+1; 47 while (l<r) 48 { 49 const int mid=(l+r)>>1; 50 if (a[star[mid]].y<a[stal[topl-1]].y) r=mid; 51 else l=mid+1; 52 } 53 down=l; 54 } 55 ans+=up-down+1; 56 // cout<<L<<' '<<R<<' '<<ord[i]<<' '<<ans<<endl; 57 } 58 int i=L,j=mid+1,k=L; 59 while (i<=mid && j<=R) 60 { 61 if (a[ord[i]].y>a[ord[j]].y) tmpord[k++]=ord[i++]; 62 else tmpord[k++]=ord[j++]; 63 } 64 while (i<=mid) tmpord[k++]=ord[i++]; 65 while (j<=R) tmpord[k++]=ord[j++]; 66 for (k=L;k<=R;k++) ord[k]=tmpord[k]; 67 } 68 69 int main() 70 { 71 scanf("%d",&n); 72 for (int i=1;i<=n;i++) scanf("%d%d",&a[i].x,&a[i].y); 73 sort(a+1,a+1+n); 74 // for (int i=1;i<=n;i++) cout<<a[i].x<<' '<<a[i].y<<endl;cout<<endl; 75 solve(1,n); 76 printf("%lld\n",ans); 77 return 0; 78 }
