cdq分治入门--BZOJ1492: [NOI2007]货币兑换Cash
n<=100000天，一开始有s块钱，每天股票A价格ai，B价格bi，每天可以做的事情：卖出股票；按A:B=RTi的比例买入股票。问最后的最大收益。股票可以为浮点数，答案保留三位。
用脚指头想想就知道是：某一天全部买进来，某一天全部卖出去，没有说买一半卖一半的。
那就可以dp了，f(i)表示前i天最大收益，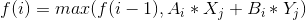
，其中Xi表示用f(i)块钱在第i天能买多少A券，Yi表示f(i)块前第i天买多少B券，可以自己算，n方过不了。
现要找max(Ai*Xj+Bi*Yj)，考虑两个状态j,k,j比k优时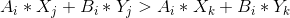
整理得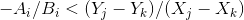
，前提是Xj>Xk
那就平衡树维护一下一个递增的(Yj-Yk)/(Xj-Xk)，即维护一个凸包即可，难写，略。
cdq就是这样把一个在线的东西强行转化成离线。
solve(l,r)表示把这个区间里的f算完，solve(l,mid)之后，用(l,mid)的状态更新(mid+1,r)的状态，然后solve(mid+1,r)，这就是一个分治。
为了使这个更新过程顺利完成，在solve(l,mid)时需要找到这个凸包，可以通过维护Xi的单调，然后直接一个栈保存单调的斜率即可；mid+1到r这一段，也需要保证-Ai/Bi的单调，这个可以预处理出来。现在就是一个离线问题，一边凸包单增被离线实现了，一边-Ai/Bi预处理排序好了，那就可以两个指针直接扫一遍更新了。
trick！！(Xj-Xk)可能等于0。。。。。。
1 #include<stdio.h> 2 #include<string.h> 3 #include<stdlib.h> 4 #include<algorithm> 5 #include<math.h> 6 //#include<iostream> 7 using namespace std; 8 9 int n,s; 10 #define maxn 200011 11 double a[maxn],b[maxn],rt[maxn]; 12 13 int num[20][maxn]; 14 void mergesort(int L,int R,int cur) 15 { 16 if (L==R) 17 { 18 num[cur][L]=L; 19 return; 20 } 21 const int mid=(L+R)>>1; 22 mergesort(L,mid,cur+1),mergesort(mid+1,R,cur+1); 23 int i=L,j=mid+1,k=i; 24 while (i<=mid && j<=R) 25 { 26 if (-a[num[cur+1][i]]/b[num[cur+1][i]]>-a[num[cur+1][j]]/b[num[cur+1][j]]) 27 num[cur][k++]=num[cur+1][i++]; 28 else num[cur][k++]=num[cur+1][j++]; 29 } 30 while (i<=mid) num[cur][k++]=num[cur+1][i++]; 31 while (j<=R) num[cur][k++]=num[cur+1][j++]; 32 } 33 34 double f[maxn],xx[maxn],yy[maxn];int sta[maxn],top,numf[20][maxn]; 35 double calc(int i,int j) {return fabs(xx[i]-xx[j])>1e-9?(yy[i]-yy[j])/(xx[i]-xx[j]):1e300;} 36 //i>j 37 void solve(int L,int R,int cur) 38 { 39 if (L==R) 40 { 41 numf[cur][L]=L; 42 f[L]=max(f[L],f[L-1]); 43 yy[L]=f[L]/(rt[L]*a[L]+b[L]); 44 xx[L]=f[L]*rt[L]/(rt[L]*a[L]+b[L]); 45 return; 46 } 47 const int mid=(L+R)>>1; 48 solve(L,mid,cur+1); 49 top=0; 50 for (int i=L;i<=mid;i++) 51 { 52 const int id=numf[cur+1][i]; 53 while (top>1 && calc(id,sta[top])-calc(sta[top],sta[top-1])>-1e-9) top--; 54 sta[++top]=id; 55 } 56 for (int i=mid+1,j=1;i<=R;i++) 57 { 58 const int &id=num[cur+1][i]; 59 while (j<top && -a[id]/b[id]-calc(sta[j+1],sta[j])<1e-9) j++; 60 f[id]=max(f[id],a[id]*xx[sta[j]]+b[id]*yy[sta[j]]); 61 } 62 solve(mid+1,R,cur+1); 63 int i=L,j=mid+1,k=i; 64 while (i<=mid && j<=R) 65 { 66 if (xx[numf[cur+1][i]]<xx[numf[cur+1][j]]) numf[cur][k++]=numf[cur+1][i++]; 67 else numf[cur][k++]=numf[cur+1][j++]; 68 } 69 while (i<=mid) numf[cur][k++]=numf[cur+1][i++]; 70 while (j<=R) numf[cur][k++]=numf[cur+1][j++]; 71 } 72 73 int main() 74 { 75 scanf("%d%d",&n,&s); 76 for (int i=1;i<=n;i++) scanf("%lf%lf%lf",&a[i],&b[i],&rt[i]); 77 mergesort(1,n,0); 78 // for (int i=0;i<=2;i++){ 79 // for (int j=1;j<=n;j++) 80 // cout<<(-a[num[i][j]]/b[num[i][j]])<<' ';cout<<endl;} 81 f[0]=s;for (int i=1;i<=n;i++) f[i]=0; 82 solve(1,n,0); 83 // for (int i=1;i<=n;i++) cout<<f[i]<<' ';cout<<endl; 84 printf("%.3f\n",f[n]); 85 return 0; 86 }
