BZOJ4558: [JLoi2016]方
n<=1e6 * m<=1e6的坐标系下求顶点不是指定的K<=2e3个点的正方形个数,%1e8+7.
一个基本的思路就是容斥,总-一个点+两个点-三个点+四个点。
总:把一个斜斜的正方形看成一个外接的正正的正方形,所以一个边长为d的正方形,顶点在他边上的正方形有d个,而边长为d的正方形在整个图上有(n-d+1)*(m-d+1)个,因此答案就是sigma d*(n-d+1)*(m-d+1)。
一个点:枚举点,先算经过他的正正的正方形:
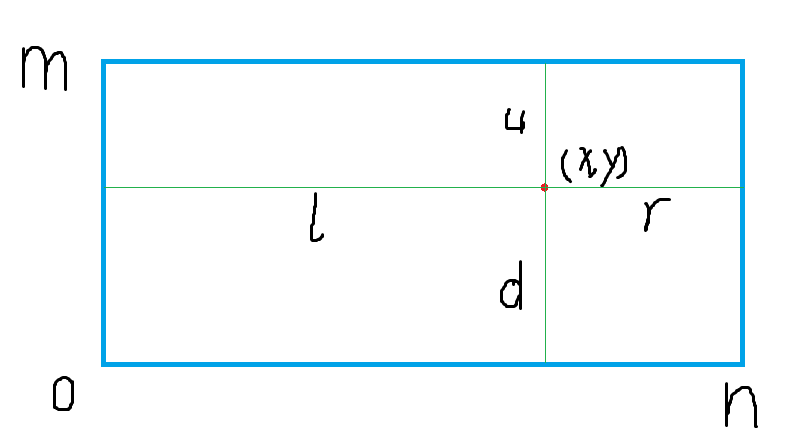
就是min(u,r)+min(d,r)+min(l,d)+min(u,d)。再算他为顶点的斜斜的。可以把这些斜斜的看成朝左,朝右,朝上,朝下的,由于计算方法一样只说朝上:
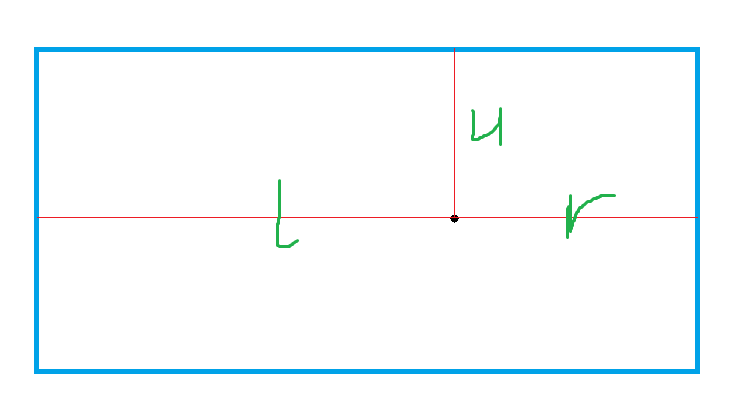
先假设u非常非常大,且l>r,观察答案随该斜斜正方形的外接正正正方形的大小的变化。
外接正正正方形大小1:0个
外接正正正方形大小2:1个
外接正正正方形大小3:2个
……
外接正正正方形大小r:r-1个
外接正正正方形大小r+1:r-1个
外接正正正方形大小r+2:r-1个
……
外接正正正方形大小l:r-1个
外接正正正方形大小l+1:r-1个
外接正正正方形大小l+2:r-2个
……
外接正正正方形大小l+r:1个
然后就没有了
实际上是一个上升、平、下降的数列,根据u的大小带不同的公式即可
两个点、三个点、四个点的情况其实只用枚举两个点就行了,因为两个点确定了一个正方形。
枚举两个点,这两个点连线可能做边长,可能做对角线,用全等三角形+解方程算出另外两个点的表达式,就可以判断这是两个点三个点还是四个点的情况了。
小技巧:枚举两个点时,由于三点情况的贡献是-1,会枚举到三次,所以每次算-1/3,加上他本身是两个点的情况,就-1/3+1=2/3,最后取整即可。四个点同理。
判断另外两个点是不是K个点中的点,哈希即可。

1 #include<cstring> 2 #include<cstdlib> 3 #include<cstdio> 4 //#include<assert.h> 5 //#include<time.h> 6 #include<math.h> 7 //#include<queue> 8 #include<algorithm> 9 //#include<iostream> 10 using namespace std; 11 12 bool isdigit(char c) {return c>='0' && c<='9';} 13 int qread() 14 { 15 char c;int s=0,f=1;while (!isdigit(c=getchar())) f=(c=='-'?-1:1); 16 do s=s*10+c-'0'; while (isdigit(c=getchar())); return s*f; 17 } 18 19 int n,m,K; 20 const int mod=1e8+7; 21 int calc(int l,int r,int h) 22 { 23 h--;int x=min(l,r),y=max(l,r); 24 if (h<=x) return 1ll*(h+1)*h/2%mod; 25 if (h<=y) return (1ll*(x+1)*x/2%mod+1ll*(h-x)*x%mod)%mod; 26 if (h<x+y) return (1ll*(x+1)*x/2%mod+1ll*(y-x)*x%mod+1ll*(x-1+x-h+y)*(h-y)/2%mod)%mod; 27 return (1ll*(x+1)*x%mod+1ll*(y-x-1)*x%mod)%mod; 28 } 29 #define maxn 2011 30 int x[maxn],y[maxn]; 31 #define maxh 10007 32 struct Hash 33 { 34 struct Node{int x,y,next;}list[maxh];int first[maxh],len; 35 Hash() {memset(first,0,sizeof(first));len=2;} 36 int hash(int x,int y) 37 { 38 return (1ll*x*19260817%maxh+1ll*y*19890604%maxh)%maxh; 39 } 40 void insert(int x,int y) 41 { 42 int v=hash(x,y); 43 list[len].x=x;list[len].y=y; 44 list[len].next=first[v];first[v]=len++; 45 } 46 int find(int x,int y) 47 { 48 if (x<0 || x>n || y<0 || y>m) return -2333; 49 int v=hash(x,y); 50 for (int i=first[v];i;i=list[i].next) 51 { 52 const Node &e=list[i]; 53 if (e.x==x && e.y==y) return 1; 54 } 55 return 0; 56 } 57 }h; 58 int main() 59 { 60 n=qread(),m=qread(),K=qread(); 61 int ans=0; 62 for (int i=1,to=min(n,m);i<=to;i++) 63 ans+=(1ll*i*(n-i+1)*(m-i+1)%mod),ans-=ans>=mod?mod:0; 64 // cout<<ans<<endl; 65 for (int i=1;i<=K;i++) 66 { 67 x[i]=qread(),y[i]=qread(); 68 int u=m-y[i],d=y[i],l=x[i],r=n-x[i]; 69 ans-=min(u,l)+min(u,r)+min(d,l)+min(d,r),ans%=mod; 70 // cout<<ans<<endl; 71 ans-=calc(l,r,u),ans%=mod; 72 ans-=calc(l,r,d),ans%=mod; 73 ans-=calc(u,d,l),ans%=mod; 74 ans-=calc(u,d,r),ans%=mod; 75 // cout<<ans<<endl; 76 ans=(ans+mod)%mod; 77 h.insert(x[i],y[i]); 78 } 79 // cout<<ans<<endl; 80 double dou=0; 81 for (int i=2;i<=K;i++) 82 for (int j=1;j<i;j++) 83 { 84 // 计算两个点的直的正方形和弯的正方形 85 int cnt;double tmp=0; 86 if ((cnt=h.find(x[i]-y[j]+y[i],y[i]+x[j]-x[i])+h.find(x[j]-y[j]+y[i],y[j]+x[j]-x[i]))==0) 87 tmp+=1; 88 else if (cnt==1) tmp+=2.0/3.0; 89 else if (cnt==2) tmp+=0.5;else{} 90 if ((cnt=h.find(x[i]+y[j]-y[i],y[i]-x[j]+x[i])+h.find(x[j]+y[j]-y[i],y[j]-x[j]+x[i]))==0) 91 tmp+=1; 92 else if (cnt==1) tmp+=2.0/3.0; 93 else if (cnt==2) tmp+=0.5;else{} 94 if (!((y[i]-y[j]+x[i]+x[j])&1) && !((x[j]-x[i]+y[i]+y[j])&1) 95 && !((x[i]+x[j]+y[j]-y[i])&1) && !((y[i]+y[j]+x[i]-x[j])&1)) 96 if ((cnt=h.find((y[i]-y[j]+x[i]+x[j])/2,(x[j]-x[i]+y[i]+y[j])/2)+ 97 h.find((x[i]+x[j]+y[j]-y[i])/2,(y[i]+y[j]+x[i]-x[j])/2))==0) 98 tmp+=1; 99 else if (cnt==1) tmp+=2.0/3.0; 100 else if (cnt==2) tmp+=0.5;else{}else{} 101 dou+=tmp; 102 } 103 printf("%lld\n",((ans+((long long)floor(dou+1e-9))%mod)+mod)%mod); 104 return 0; 105 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号