BZOJ3302: [Shoi2005]树的双中心
n<=50000的树，深度<=100，有点权，选两个点x，y，使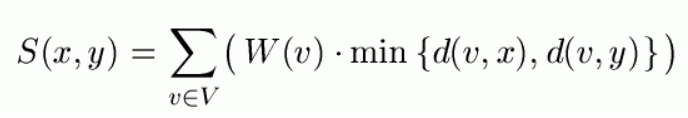
最小。
dis取了min之后，整个树就会以某条边为分界线分成两半，一半归一个点管。如果是两棵完全独立的树的话，那肯定分别取这两棵树的带权重心。但割掉某条边再找两边重心，这种情况不一定是合法情况。例如：
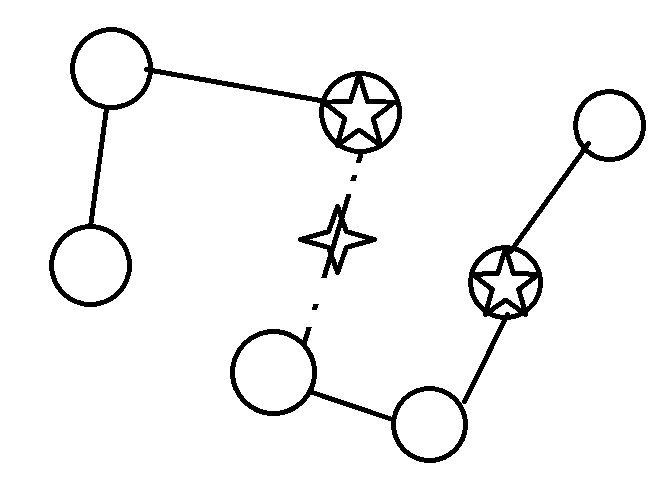
上图中，虚线边被断开，两边的重心分别是星标节点。这不是一个合法方案，但它显然不如一个合法方案的答案优：
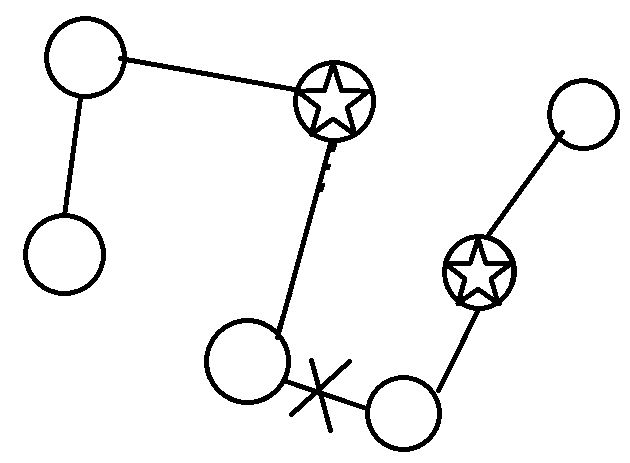
所以放心大胆地割就好了。注意到本题中树的深度h很小，所以割边后涉及的子树信息修改操作都可以暴力修改。
把树以某点为根，希望能预处理出一些信息使得能够在O(h)的时间内找到割完边每一半的重心。如果是普通的一棵树，知道了子树大小（权值和）之后，从某点出发最多走2h步之后就可以到重心。割了某条边之后，一个点最多只会有一棵子树信息被修改。因此记最大儿子和次大儿子即可。
至于答案的记录我写的有点丑。如果想的话可以看一下我怎么写的，不然就直接看怎么写更方便吧。所有子树大小加起来即为根节点为重心的总代价，因为这样加起来，越是下面的点加的次数越多。断掉某条边之后，修改子树大小的同时可修改根节点为重心答案，然后从根节点开始向重儿子走，只要比较最大儿子和次大儿子子树权和即可，边走边改答案。走一步，就是走到的这棵子树权值和少算一次，其外面的权值和多算一次。
我是记了每个节点为根的答案。。式子有点乱。。
1 #include<stdio.h> 2 #include<string.h> 3 #include<stdlib.h> 4 #include<algorithm> 5 //#include<queue> 6 //#include<iostream> 7 using namespace std; 8 9 int t,n; 10 #define maxn 50011 11 struct Edge{int to,next;}edge[maxn<<1];int first[maxn],le,val[maxn]; 12 void in(int x,int y) {Edge &e=edge[le];e.to=y;e.next=first[x];first[x]=le++;} 13 void insert(int x,int y) {in(x,y);in(y,x);} 14 void init() 15 { 16 scanf("%d",&n); 17 memset(first,0,sizeof(first));le=2; 18 int x,y; 19 for (int i=1;i<n;i++) 20 { 21 scanf("%d%d",&x,&y); 22 insert(x,y); 23 } 24 for (int i=1;i<=n;i++) scanf("%d",&val[i]); 25 } 26 #define LL long long 27 int size[maxn],dep[maxn],f[maxn],tot,hea[maxn],h2[maxn];LL aa[maxn]; 28 void dfs(int x,int fa) 29 { 30 size[x]=val[x];dep[x]=dep[fa]+1;f[x]=fa;tot+=val[x]; 31 hea[x]=h2[x]=0;aa[x]=0; 32 for (int i=first[x];i;i=edge[i].next) 33 { 34 const Edge &e=edge[i];if (e.to==fa) continue; 35 dfs(e.to,x);size[x]+=size[e.to]; 36 aa[x]+=aa[e.to]+size[e.to]; 37 if (size[e.to]>size[hea[x]]) h2[x]=hea[x],hea[x]=e.to; 38 else if (size[e.to]>size[h2[x]]) h2[x]=e.to; 39 } 40 } 41 int main() 42 { 43 init(); 44 tot=0;dfs(1,0); 45 LL ANS=1e15; 46 for (int i=2;i<le;i+=2) 47 { 48 int x=edge[i].to,y=edge[i^1].to; 49 if (dep[x]<dep[y]) {int t=x;x=y;y=t;} 50 for (int i=f[x],cnt=1;i;i=f[i],cnt++) size[i]-=size[x],aa[i]-=aa[x]+1ll*cnt*size[x]; 51 tot-=size[x]; 52 LL ans=0,qq=0; 53 for (int now=1;;) 54 { 55 int tmp=(hea[now]==x?(h2[now]?size[h2[now]]:0):(h2[now]==x?size[hea[now]]: 56 max(size[hea[now]],size[h2[now]])))*2; 57 58 if (tmp<=tot) {ans+=aa[now]+qq;break;} 59 if (size[hea[now]]>size[h2[now]] && hea[now]!=x) now=hea[now], 60 qq+=aa[f[now]]-(aa[now]+size[now])+tot-size[now]; 61 else now=h2[now],qq+=aa[f[now]]-(aa[now]+size[now])+tot-size[now]; 62 } 63 qq=0; 64 for (int now=x;;) 65 { 66 if (size[hea[now]]*2<=size[x]) {ans+=aa[now]+qq;break;} 67 now=hea[now],qq+=aa[f[now]]-(aa[now]+size[now])+size[x]-size[now]; 68 } 69 ANS=min(ANS,ans); 70 tot+=size[x]; 71 for (int i=f[x],cnt=1;i;i=f[i],cnt++) size[i]+=size[x],aa[i]+=aa[x]+1ll*cnt*size[x]; 72 } 73 printf("%lld\n",ANS); 74 return 0; 75 }
