Dilworth's theorem (by wikipedia) - BloodElf

公告

In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem characterizes the width of any finite partially ordered set in terms of a partition of the order into a minimum number of chains. It is named for the mathematician Robert P. Dilworth.

An antichain in a partially ordered set is a set of elements no two of which are comparable to each other, and a chain is a set of elements every two of which are comparable. Dilworth's theorem states that there exists an antichain A, and a partition of the order into a family P of chains, such that the number of chains in the partition equals the cardinality of A. When this occurs, A must be the largest antichain in the order, for any antichain can have at most one element from each member of P.

Similarly, P must be the smallest family of chains into which the order can be partitioned, for any partition into chains must have at least one chain per element of A. The width of the partial order is defined as the common size of A and P.

An equivalent way of stating Dilworth's theorem is that, in any partially ordered set, the maximum number of elements in any antichain equals the minimum number of chains in any partition of the set into chains.

The following proof by induction on the size of $P$ is based on that of Galvin (1994).

Let $P$ be a finite partially ordered set. The theorem holds trivially if $P$ is empty. So, assume that $P$ has at least one element, and let $a$ be a maximal element of $P$ .

By induction, we assume that for some integer $k$ the partially ordered set $P':=P\setminus\{a\}$ can be covered by $k$ disjoint chains $C_1,\dots,C_k$ and has at least one antichain $A 0$ of size $k$ .

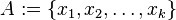Clearly, $A_0\cap C_i\ne\emptyset$ for $i=1,2,\dots,k$ . For $i=1,2,\dots,k$ , let $x i$ be the maximal element in $C i$ that belongs to an antichain of length $k$ in $P'$ , and set $\text{[math]}$ . We claim that $A$ is an antichain. Let $A 1$ be an antichain of length $k$ that contains $x 1$ . Then $A_1\cap C_2\ne\emptyset$ . Let $y\in A_1\cap C_2$ . Then $y\le x_2$ , by the definition of $x 2$ . 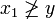This implies that $x_1\not \ge x_2$ , since $x_1\not\ge y$ . Similarly, we have $x_i\not\ge x_j$ for all 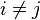$i\ne j$ in $\{1,2,\dots,k\}$ , verifying that $A$ is an antichain.

We now return to $P$ . Suppose first that $a\ge x_i$ for some $i\in\{1,2,\dots,k\}$ . Let $K$ be the chain $\{a\}\cup\{z\in C_i:z\le x_i\}$ . Then by the choice of $x i$ , $P\setminus K$ does not have an antichain of length $k$ . Induction then implies that $P\setminus K$ can be covered by $k - 1$ disjoint chains. Thus, $P$ can be covered by $k$ disjoint chains, as required. 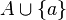Next, if $a\not\ge x_i$ for each $i\in\{1,2,\dots,k\}$ , then $A\cup\{a\}$ is an antichain of length $k + 1$ in $P$ (since $a$ is maximal in $P$ ). Because $P$ can be covered by the $k + 1$ chains $\{a\},C_1,C_2,\dots,C_k$ , this completes the proof.

posted on 2010-03-16 14:33 BloodElf 阅读(234) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

织梦行云

公告