实验——树(根据后序和中序遍历输出先序遍历、哈夫曼编码)详细过程
实验——树(根据后序和中序遍历输出先序遍历、哈夫曼编码)
一、实验目的
-
熟练掌握二叉树、完全二叉树的存储方式,二叉树的前序、中序、后序和层次遍历方法,树的性质。
-
练习建立二叉树的算法,通过前中、后中顺序确定二叉树的算法。
-
通过二叉树的算法,解决哈夫曼编码等应用问题。
二、 根据后序和中序遍历输出先序遍历
2.1 实验内容和要求
问题描述
输入格式
第一行给出正整数N(≤30),是树中结点的个数。随后两行,每行给出N个整数,分别对应后序遍历和中序遍历结果,数字间以空格分隔。题目保证输入正确对应一棵二叉树。
输出格式
在一行中输出Preorder: 以及该树的先序遍历结果。数字间有1个空格,行末不得有多余空格。
输入样例
7 2 3 1 5 7 6 4 1 2 3 4 5 6 7
输出样例
Preorder: 4 1 3 2 6 5 7
2.2 算法设计
-
主流程设计
int main(){ 输入树中结点个数; 输入该树的后序遍历结果; 输入该树的中序遍历结果; 通过两种遍历结果创建该树; 用先序遍历方法输出该树; return 0; }
2. 构建二叉树流程分析
*设计思路:通过后序遍历找到该树的根结点(即后序遍历最后一个结点),根结点将中序遍历序列分为两个子序列,就可以确定根结点下的左右子树的结点个数,且后序遍历序列可以看作根结点左子树序列+根结点右子树序列+根结点组成。由树的递归性可以对根结点左子树序列、根结点右子树序列进行相同操作。
*具体实现:设定两序列长度均为Len,后序遍历序列为Post,中序遍历序列为In,在递归过程中后序遍历序列区间为[k,Len-1],中序遍历序列区间为[k,Len-1],由上述分析可以知道,在这一递归阶段中,根结点为Post[Len-1], 接着在中序遍历序列中寻找位置index,使In[index] = Post[Len-1],这样这一递归阶段中左子树结点数量为i, 进入下一递归阶段时,左子树后序遍历序列和中序遍历序列变为[k, i-1],右子树后序遍历序列变为[k+i, Len-i-1],中序遍历序列变为[k+i+1, Len-i-1](‘+1’是该树的根结点的位置,需要跳过去)。
BinTree CreateBinTree(int* Post, int* In, int Len) { //输入后序、中序和结点的个数 判断是否有子树; 创建树; 将此时后序遍历的最后一个数作为一个根结点; 遍历中序结果; 若找到与根结点相同的数,将该数下标做标记,并且跳出循环; 找根结点的左子树; 找根结点右子树的值; }
-
ADT定义
typedef struct TNode* PreToTNode; struct TNode { int Data; PreToTNode Left; PreToTNode Right; }; typedef PreToTNode BinTree; //根据前序和中序遍历,构建二叉树 BinTree CreateBinTree(int* Post, int* In, int Len); //先序遍历输出 void PreorderTraversal(BinTree BT);
-
算法示例
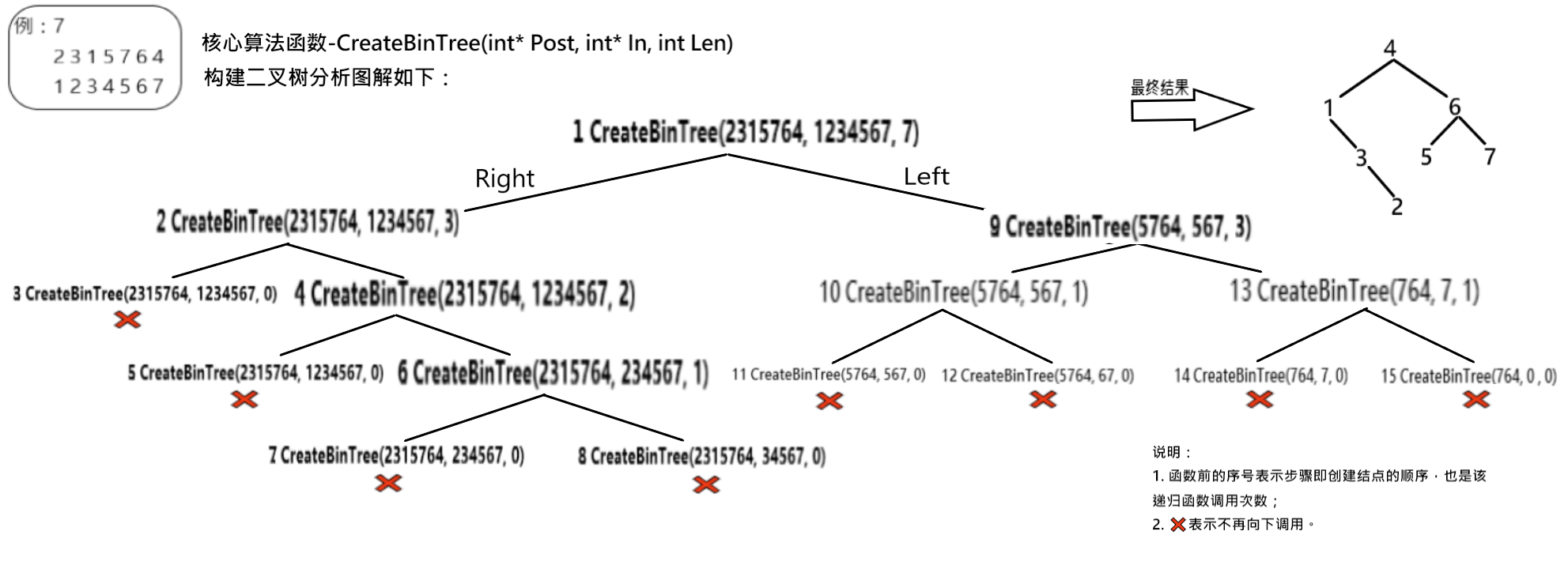
2.3 算法分析
通过算法过程示例发现,时间复杂度为 O(n) = O(NlogN[构建二叉树] + NlogN[先序遍历输出]) = O(2*NlogN) ;
空间复杂度为二叉树 的构造空间使用 O(n) = O(N)。
三、哈夫曼编码
3.1 实验内容和要求
问题描述
给定一段文字,如果我们统计出字母出现的频率,是可以根据哈夫曼算法给出一套编码,使得用此编码压缩原文可以得到最短的编码总长。然而哈夫曼编码并不是唯一的。例如对字符串"aaaxuaxz",容易得到字母 'a'、'x'、'u'、'z' 的出现频率对应为 4、2、1、1。我们可以设计编码 {'a'=0, 'x'=10, 'u'=110, 'z'=111},也可以用另一套 {'a'=1, 'x'=01, 'u'=001, 'z'=000},还可以用 {'a'=0, 'x'=11, 'u'=100, 'z'=101},三套编码都可以把原文压缩到 14 个字节。但是 {'a'=0, 'x'=01, 'u'=011, 'z'=001} 就不是哈夫曼编码,因为用这套编码压缩得到 00001011001001 后,解码的结果不唯一,"aaaxuaxz" 和 "aazuaxax" 都可以对应解码的结果。本题就请你判断任一套编码是否哈夫曼编码。
输入格式
首先第一行给出一个正整数 N(2≤N≤63),随后第二行给出 N 个不重复的字符及其出现频率,格式如下:
c[1] f[1] c[2] f[2] ... c[N] f[N]
其中c[i]是集合{'0' - '9', 'a' - 'z', 'A' - 'Z', '_'}中的字符;f[i]是c[i]的出现频率,为不超过 1000 的整数。再下一行给出一个正整数 M(≤1000),随后是 M 套待检的编码。每套编码占 N 行,格式为:
c[i] code[i]
其中c[i]是第i个字符;code[i]是不超过63个'0'和'1'的非空字符串。
输出格式
对每套待检编码,如果是正确的哈夫曼编码,就在一行中输出"Yes",否则输出"No"。 注意:最优编码并不一定通过哈夫曼算法得到。任何能压缩到最优长度的前缀编码都应被判为正确。
输入样例
7 A 1 B 1 C 1 D 3 E 3 F 6 G 6 4 A 00000 B 00001 C 0001 D 001 E 01 F 10 G 11 A 01010 B 01011 C 0100 D 011 E 10 F 11 G 00 A 000 B 001 C 010 D 011 E 100 F 101 G 110 A 00000 B 00001 C 0001 D 001 E 00 F 10 G 11
输出样例
Yes
Yes
No
No
3.2 算法设计
-
主流程设计
int main(){ 建一个哈夫曼树; 将字符存进去; 计算最优WPL; 读入待检测的编码; 比较编码的wpl是否与最优WPL一致; 检测是否是前缀编码; }
2. 哈夫曼树的构造
*设计思路:由哈夫曼树和带权路径长度的定义可知,一棵二叉树要使其WPL最小,必须使权值越大的叶结点越靠近根结点,而权值越小的叶结点越远离根结点。可在初始状态下将每一个字符看成一棵独立的树,每一步选择权值最小的两颗树进行合并。
初始化哈夫曼树; for(遍历前n个){ 存叶子节点,赋给权值,其他项(parent、lchild、rchild)赋零; } for(遍历后面的){ 存非叶子节点,权值赋零,其他项也赋零; } 建立哈夫曼树; for(遍历每套编码方案){ 在HT[1,i-1]中找到没有parent且权值最小的两个元素(需要一个函数); 将其parent、lchild、rchlid赋值,并算该树的权值,一步一步建立哈夫曼树; }
注意根结点的位置变化;
}
3. 最优带权路径长度(WPL)的求值
*设计思路:计算该树的最优带权路径长度,用来判断所给编码方案是否为最优编码。 具体实现:运用递归函数,由根结点依次向下找出叶节点。
void GetWPL(HuffmanTree HT, int Deep, HTNode* p){ //对叶子节点进行计算 if ((p->lchild == 0) && (p->rchild == 0)){ WPL += (p->weight) * Deep; } if (p->lchild != 0) //注意细节,不能用 else if GetWPL(HT, Deep + 1, HT + (p->lchild)); if (p->rchild != 0) GetWPL(HT, Deep + 1, HT + (p->rchild)); }
-
前缀编码的判断 * 设计思路:前缀编码是指任一字符的编码都不是另一个字符编码的前缀(等长编码一定是前缀编码!)。由于需要编码及其地址,所以运用二维数组的传递更为方便。 *具体实现:将这些编码逐个的添加到二维数组中,对于每一个编码字符串,字符串中的每一个字符也逐个扫描(需要注意循环开始的条件),先假定不是前缀编码,用flag记录,两两相比较,如果在循环中有不一样的编码位,说明是前缀编码;如果循环结束但已扫描到某节点为叶子节点但字符串还未结束,或者字符串已扫描结束但还当前节点非空,那么就不是前缀码。
int IsPreCoding(char temp[][64]){ int i, j, h, len1, len2; for (i = 1; i <= N - 1; ++i){ for (j = i + 1; j <= N; ++j){ //j和i为需要比较的元素下标 int flag = 0; for (h = 0; (temp[i][h] != '\0') && (temp[j][h] != '\0'); h++){ if (temp[i][h] != temp[j][h]){ flag = 1; } } if (flag == 0){ return 0; } } } return 1; }
-
ADT定义
int m; //哈夫曼树节点个数 int w[64], N, M; //权值数组W[],元素数量N,M套编码 int WPL; //带权路径长度 typedef struct HTNode* HuffmanTree; struct HTNode{ int weight; //结点权值 int parent, lchild, rchild; }; HTNode* Root_pos; typedef char** HuffmanCode; //定义元素类型为 char数组首地址 的数组 void Select(HuffmanTree& HT, int n, int& s1, int& s2); //比较权值,找出最小、次小权值 void HuffmanCoding(HuffmanTree& HT, HuffmanCode& HC, int* w, int n); //构造哈夫曼树 int IsPreCoding(char temp[][64]); //判断是否为前缀编码 void GetWPL(HuffmanTree HT, int Deep, HTNode* p); //对叶子节点进行计算,求WPL
2.3 算法分析
该Huffman算法的复杂度主要由以下几部分组成:
(1)构造哈夫曼树:O(N^2);
(2)求最优WPL: O(NlogN);
(3)前缀编码的判断:O(N^2);
故整体复杂度为 O(n) = (NlogN) ;
空间复杂度为结点空间的使用,即O(N)。
四、总结
根据后序和中序遍历输出先序遍历:
主要不清楚的点在构建树的左右子树的递归函数中后序序列、中序序列和根结点、长度的关系,根据例子画图,按照还原后的二叉树反过来一步一步带入到函数中,最后再正着分析才明白;
哈夫曼编码:
虽然知道如何求WPL、哈夫曼编码怎么构建,但也只是头脑中的动画演示,代码写不出来,于是在网上找到了代码做思考分析。这个代码思路特别清晰,难理解的是其使用的方法,例如运用二维数组的传递判断是否为前缀编码,不知道为什么用二维数组、为什么不用一维或者直接扫描或者其他容器,经过反复研读代码,做了些小试验,体会到了运用二维数组传递的简洁,还有其他一些不懂的,又重新多看了几遍慕课和书本相关内容。在整个分析中发现自己更多的问题,特别是树、指针、地址、数组等的灵活运用,还有代码的理解能力等,感觉还有一些没有想到的问题与分析。这是一道经典题,需要强加记忆、反复思考,需要勤加锻炼、多动手打代码,需要反复修改;
通过这两道题:
书、慕课、CSDN、画图或者动画演示等都是为自己能够记住、能够自己打出成功代码而服务的,不要认为理解了、能十分详细的用图的形式解释明白就完事了的,还需要再看反复看,会有新的认识,对自己写代码就会有更多的帮助。
五、源代码(主要)
5.1 根据后序和中序遍历输出先序遍历
/* 先序递归遍历 *访问根结点 *先序遍历其左子树 *先序遍历其右子树 */ void PreorderTraversal(BinTree BT) { if (BT) { printf(" %d", BT->Data); PreorderTraversal(BT->Left); PreorderTraversal(BT->Right); } } /* 构建树 *输入后序、中序和结点的个数 */ BinTree CreateBinTree(int* Post, int* In, int Len) { BinTree T; int index = 0; if (Len == 0) { //判断是否有子树 return NULL; } T = (BinTree)malloc(sizeof(struct TNode)); //创建树 T->Data = Post[Len - 1]; //此时后序遍历的最后一个数作为一个根结点 for (int i = 0; i < Len; i++) { //遍历中序结果 if (In[i] == Post[Len - 1]) { //若找到与根结点相同的数,将该数下标做标记,跳出循环 index = i; break; } } T->Left = CreateBinTree(Post, In, index); //找根结点的左子树 T->Right = CreateBinTree(Post + index, In + index + 1, Len - index - 1); //找根结点右子树的值 return T; }
5.2 哈夫曼编码
/*找最小、次小权值*/ void Select(HuffmanTree& HT, int n, int& s1, int& s2){ int i; s1 = s2 = 0; int min1 = INT_MAX; //最小值,INT_MAX在<limits.h>中定义的 int min2 = INT_MAX; //次小值 for (i = 1; i <= n; ++i){ if (HT[i].parent == 0){ //找没有parent的最小和次小权值(下标) //只有两种情况 if (HT[i].weight < min1){ min2 = min1; //旧的最小权值赋给旧的次小权值 s2 = s1; //下标变动 min1 = HT[i].weight; //赋最小权值 s1 = i; } else if ((HT[i].weight >= min1) && (HT[i].weight < min2)){ min2 = HT[i].weight; //赋次小权值 s2 = i; } } } } void HuffmanCoding(HuffmanTree& HT, HuffmanCode& HC, int* w, int n){ if (n <= 1) return; M = 2 * n - 1; HuffmanTree p; int i; HT = (HuffmanTree)malloc((M + 1)*sizeof(HTNode)); //初始化哈夫曼树 w++; for (p = HT + 1, i = 1; i <= n; ++i, ++p, ++w){ //前n个存叶子节点,赋权值,其他项赋零 p->weight = *w; p->parent = 0; p->lchild = 0; p->rchild = 0; } for (; i <= M; ++i, ++p){ //后面存非叶子节点; p->weight = 0; p->parent = 0; p->lchild = 0; p->rchild = 0; } //建立哈夫曼树 int s1, s2; for (i = n + 1; i <= M; i++){ Select(HT, i - 1, s1, s2); //此函数在HT[1,i-1]中选择父为零且w值最小的两个元素,返回下标 HT[s1].parent = i; HT[s2].parent = i; HT[i].lchild = s1; HT[i].rchild = s2; HT[i].weight = HT[s1].weight + HT[s2].weight; } Root_pos = (HT + i - 1); } /*前缀编码的判断*/ int IsPreCoding(char temp[][64]){ int i, j, h, len1, len2; for (i = 1; i <= N - 1; ++i){ //循环比较N-1次 for (j = i + 1; j <= N; ++j){ //j和i为需要比较的元素下标 int flag = 0; //假定不是前缀编码 for (h = 0; (temp[i][h] != '\0') && (temp[j][h] != '\0'); h++){ if (temp[i][h] != temp[j][h]){ //循环中有不一样的编码位,说明是前缀编码 flag = 1; } } if (flag == 0){ //如果循环结束flag还没有变,说明当前的两个不是前缀编码,返回0 return 0; } } } return 1; } //递归求WPL void GetWPL(HuffmanTree HT, int Deep, HTNode* p){ //对叶子节点进行计算 if ((p->lchild == 0) && (p->rchild == 0)){ WPL += (p->weight) * Deep; } if (p->lchild != 0) GetWPL(HT, Deep + 1, HT + (p->lchild)); if (p->rchild != 0) GetWPL(HT, Deep + 1, HT + (p->rchild)); } int main(){ /*处理哈夫曼树*/ cin >> N; char ch; int i; for (i = 1; i <= N; i++){ cin >> ch >> w[i]; } HuffmanTree HT; HuffmanCode HC, HCp; HuffmanCoding(HT, HC, w, N); /*得出权值最优路径*/ int Deep = 0; HTNode* p = Root_pos; WPL = 0; GetWPL(HT, Deep, p); /*处理编码方案*/ cin >> M; for (int j = 0; j < M; j++){ //M套编码方案 int wpl = 0; char temp[N + 2][64]; //注意开二维数组,下面每个循环用一维 for (i = 1; i <= N; i++){ //每套编码都是N个元素 cin >> ch >> temp[i]; wpl += (strlen(temp[i]) * w[i]); } if (wpl > WPL){ //判断是否是最优编码 cout << "No" << endl; }else{ if (IsPreCoding(temp)){ //判断是否是前缀编码 cout << "Yes" << endl; }else{ cout << "No" << endl; } } } getchar(); return 0; }
算法分析、遍历生成树分析图等均为原创作品,欢迎指正!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号