线性结构实验 —— 堆栈、队列（汉诺塔的非递归实现）详细过程

线性结构实验 —— 堆栈、队列（汉诺塔的非递归实现）

一、实验目的

熟练掌握堆栈、队列的两种存储结构实现方式及操作。
练习使用堆栈、队列结构解决问题的能力。
通过算法分析掌握不同存储结构的操作特点。

二、实验内容和要求

问题描述

汉诺塔的非递归实现借助堆栈以非递归（循环）方式求解汉诺塔的问题（n, a, b, c），即将N个盘子从起始柱（标记为“a”）通过借助柱（标记为“b”）移动到目标柱（标记为“c”），并保证每个移动符合汉诺塔问题的要求。

输入格式

输入为一个正整数N，即起始柱上的盘数。

输出格式

每个操作（移动）占一行，按柱1 -> 柱2的格式输出。

输入样例

输出样例:

a -> c 
a -> b
c -> b
a -> c 
b -> a 
b -> c 
a -> c

三、算法分析

1. 主流程设计

int main {
  输入起始柱上的盘数;
  通过借助柱移动盘子到目标柱;
  输出盘子从起始柱通过借助柱移动到目标柱的详细步骤;
  return 0;
 }

2. ADT定义

struct Node //将栈内元素放入一个结构体中
 {
   char start; //起始柱
   char mid; //借助柱
   char goal; //目标柱
   int num; //起始柱上的盘数
 };
typedef int Position; //栈顶位置
typedef struct Node ElementType; //将堆栈的元素类型具体化
//typedef enum { false, true } bool;
/*堆栈的顺序表定义*/
 typedef struct SNode* PtrToSNode;
 struct SNode
 {
   ElementType* data; //存储元素的数组
   Position Top; //堆栈的栈顶指针
   int Maxsize; //堆栈的最大容量
 };
 typedef PtrToSNode Stack;
Stack CreateStack();
 bool IsFull(Stack S);
 bool push(Stack S, int n, char a, char b, char c);
 bool IsEmpty(Stack S);
 ElementType pop(Stack S);

3. 移动流程分析

设计思路：首先起始柱上除了底盘的其他盘子，需要通过目标柱移动到借助柱上，将此时的借助柱看作“目标柱”，将此时的目标柱看作“借助柱”压栈，栈满，不再执行下一次压栈（之后也是如此），然后将起始柱的底盘移动到目标柱上，最后将借助柱上的盘子通过起始柱移动到目标柱。

while(堆栈不为空)
 {
   弹出栈顶元素;
   if (元素的num为1)
    直接输出;
   else
    /*移动柱子相当于移动柱子上在最上面的盘子*/
     当最底下的大盘到达目标柱，而其余的在借助柱时，压栈将借助柱和目标柱调换位置，达到盘子到达目标柱的目的；
     当只剩下一个盘子没有到目标柱时，压栈将目标柱和起始柱调换位置，达到盘子到达目标柱的目的;
     将盘子除了最底下的大盘移动到借助柱时，压栈将此时的借助柱作为目标柱，目标柱作为借助柱；
 }
 当操作数处理完毕后，运算符栈弹空;

4. 算法示例

当 n=3 即只有三个盘子时，如下为具体移动步骤图画展示：

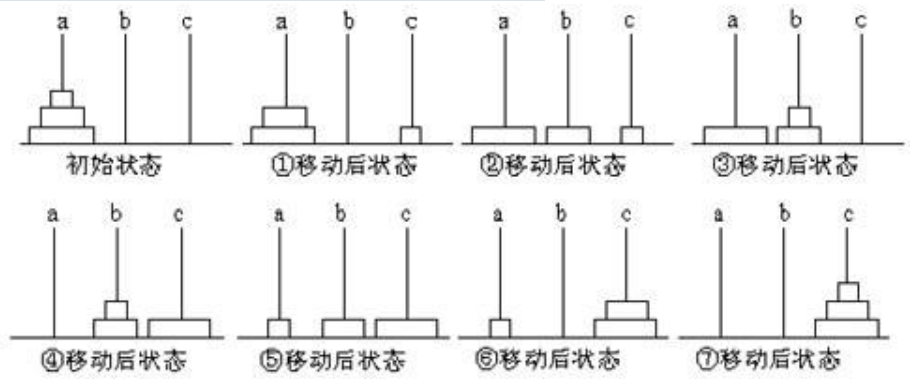
下图为堆栈内的详细情况：

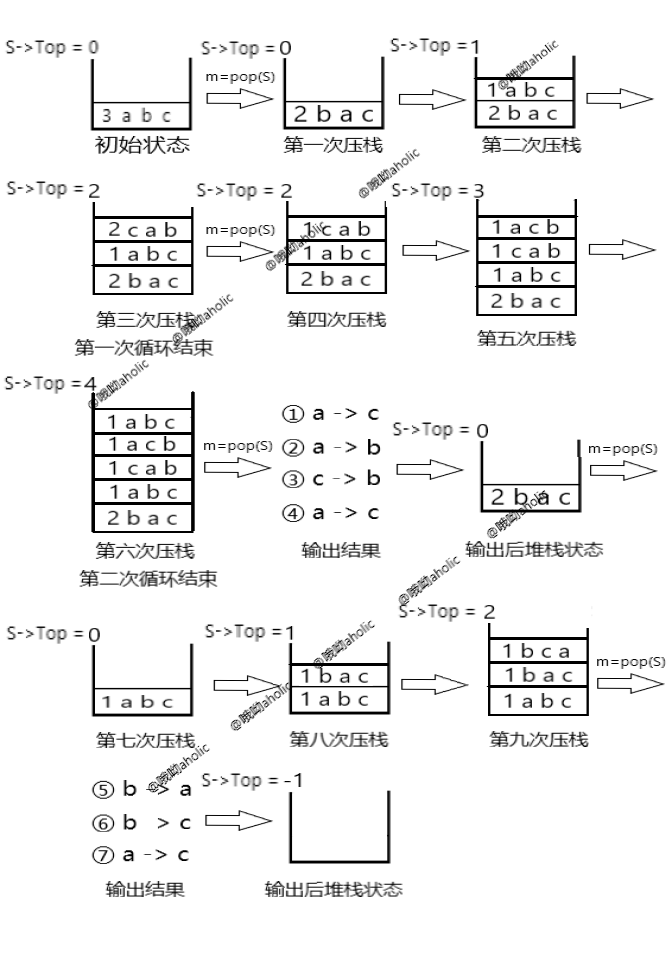
5. 算法示例（假设盘子的个数为3）

四、算法分析

通过算法过程示例发现，时间复杂度为 O(n) = (2^N) ，空间复杂度为柱子栈空间的使用，O(1)。

五、总结

设计算法时，总从它的递归方向去想，写出来的程序感觉隐约是递归，最后决定从递归实现改到非递归实现，即将主函数压栈的程序移出展开，没有注意弹栈后需要再次压栈才能移动原来的柱子，造成输出步骤缺失错误。在画图的时候，虽然明白移盘子的详细过程，但是堆栈进出的顺序和压栈的数量值还是模糊的，通过在代码程序中加断点用Debug，一点一点分析推导并画出来，才更加清晰。

六、源代码（附汉诺塔递归主函数代码）

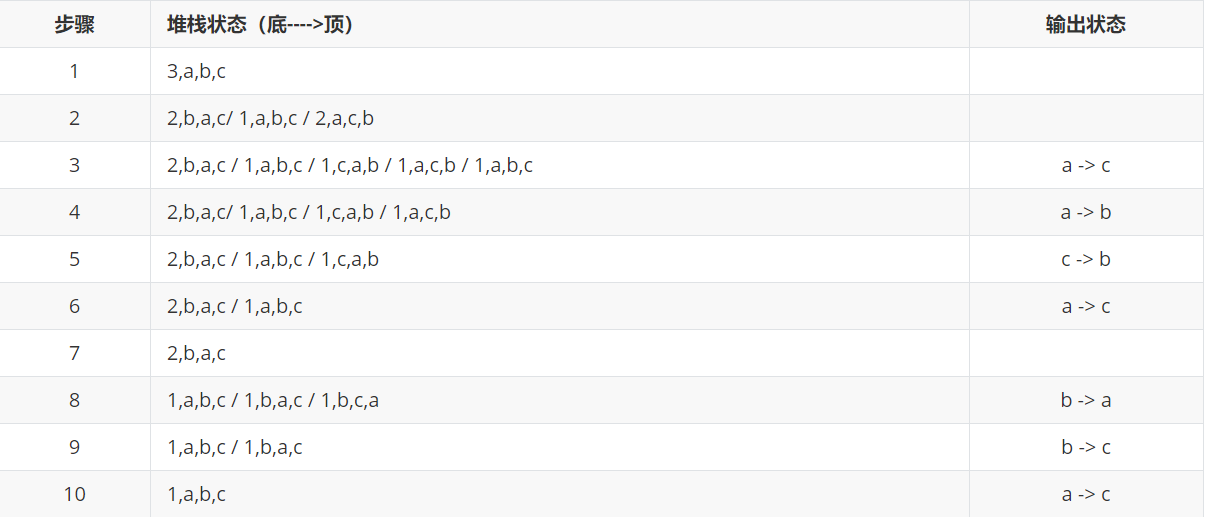
/*借助栈的非递归实现*/#include <stdio.h>
#include<stdlib.h>

struct Node  //将栈内元素放入一个结构体中
{
    char start; //起始柱
    char mid; //借助柱
    char goal;  //目标柱
    int num; //起始柱上的盘数
};


typedef int Position; //栈顶位置
typedef struct Node ElementType; //将堆栈的元素类型具体化
//typedef enum { false, true } bool;

/*堆栈的顺序表定义*/
typedef struct SNode* PtrToSNode;
struct SNode
{
    ElementType* data; //存储元素的数组
    Position Top; //堆栈的栈顶指针
    int Maxsize; //堆栈的最大容量
};
typedef PtrToSNode Stack;


bool push(Stack S, int n, char a, char b, char c);
ElementType pop(Stack S);

/*
生成空堆栈，其最大长度为 Maxsize
*/
Stack CreateStack() {
    Stack S;
    S = (Stack)malloc(sizeof(struct SNode));
    S->Maxsize = 1000;
    S->data = (struct Node*)malloc(S->Maxsize * sizeof(struct Node));
    S->Top = -1;
    return S;
}

/*
判断堆栈S是否已满。
若S中元素个数等于 Maxsize 时返回 TRUE
否则返回 FALSE
*/
bool IsFull(Stack S) {
    return (S->Top == S->Maxsize - 1);
}
/*
将元素压入堆栈。
若堆栈已满，返回 FALSE
否则将数据元素插入到堆栈 S 栈顶，返回 TRUE
*/
bool push(Stack S, ElementType X)
{
    if (IsFull(S)) {
        printf("Full Stack.\n");
       return false;
   }
    else {
    /*S->Top++;
    S->data[S->Top].start = a;
    S->data[S->Top].mid = b;
    S->data[S->Top].goal = c;
    S->data[S->Top].num = n;*/
    S->data[++(S->Top)] = X;
    return true;
    }
}
/*
判断堆栈 S 是否为空。
若是返回 TRUE
否则返回 FALSE
*/
bool IsEmpty(Stack S) {
    return (S->Top == -1);
}
/*
删除并返回栈顶元素。
若堆栈为空，返回错误信息
否则将栈顶数据元素从堆栈中删除并返回
*/
ElementType pop(Stack S)
{
    if (IsEmpty(S)) {
        printf("Empty Stack.\n");
        ElementType e;
        e.num = -1;
        return e;
    }
    else
        return S->data[S->Top--];
}

/*借助栈的非递归实现*/
int main()
{
    int n;
    scanf_s("%d", &n);
    Stack S;
    S = CreateStack();
    struct Node m; //相当于ElementType m;
    m.start = 'a';
    m.mid = 'b';
    m.goal = 'c';
    m.num = n;
    push(S, m);  //将初始状态压栈
    while (S->Top >= 0)  //堆栈不空
    {
        m = pop(S); //弹出栈顶元素
        if (m.num == 1)
        {
           printf("%c -> %c\n", m.start, m.goal);
        }
        else
        {
            /* n-1个盘，从辅助柱，借助源柱，移动到目标柱 */
            //push(S, m.num - 1, m.mid, m.start, m.goal);
            push(S, S->data[S->Top]);
            S->data[S->Top].num = m.num - 1;
            S->data[S->Top].start = m.mid;
            S->data[S->Top].mid = m.start;
            S->data[S->Top].goal = m.goal;
            
            
            /* 最后一个盘，从源柱，借助辅助柱，移动到目标柱 */
            //push(S, 1, m.start, m.mid, m.goal);
            push(S, S->data[S->Top]);
            S->data[S->Top].num = 1;
            S->data[S->Top].start = m.start;
            S->data[S->Top].mid = m.mid;
            S->data[S->Top].goal = m.goal;

            
            /* n-1个盘，从源柱，借助目标柱，移动到辅助柱 */
            //push(S, m.num - 1, m.start, m.goal, m.mid);
            push(S, S->data[S->Top]);
            S->data[S->Top].num = m.num - 1;
            S->data[S->Top].start = m.start;
            S->data[S->Top].mid = m.goal;
            S->data[S->Top].goal = m.mid;
            
  
        }
    }
    return 0;
}

 /*借助栈的递归实现*/
 int main()
 {
   int n;
   scanf_s("%d", &n);
   Stack S;
   S = CreateStack();
   struct Node m;
   push(S, n, 'a', 'b', 'c'); //将初始状态压栈
   while (S->Top >= 0)
   {
     m = pop(S);
     if (m.num == 1)
     {
       printf("%c -> %c\n", m.start, m.goal);
     }
     else
     {
       /* n-1个盘，从借助柱，借助起始柱，移动到目标柱 */
       push(S, m.num - 1, m.mid, m.start, m.goal);
       /* 最后一个盘，从起始柱，借助借助柱，移动到目标柱 */
       push(S, 1, m.start, m.mid, m.goal); 
       /* n-1个盘，从起始柱，借助目标柱，移动到借助柱 */
       push(S, m.num - 1, m.start, m.goal, m.mid);
     }
   }
   return 0;
 }

算法分析、堆栈分析图等均为原创作品，欢迎指正！

posted @ 2020-10-31 21:28 哦呦aholic 阅读(963) 评论(0) 收藏举报

刷新页面返回顶部

哦呦aholic