SPOJ687 Repeats

本篇是罗穗骞《后缀数组——处理字符串的有力工具》的读书笔记。

知识点：　　后缀数组、RMQ

解题思路：

　　枚举长度 \(L\)，然后检查长度为 \(L\) 的子串最多能连续重复几次。

　　对于给定的字符串 \(S\)，我们只关注其上坐标为 \(0, L, 2L, ......\) 的点。

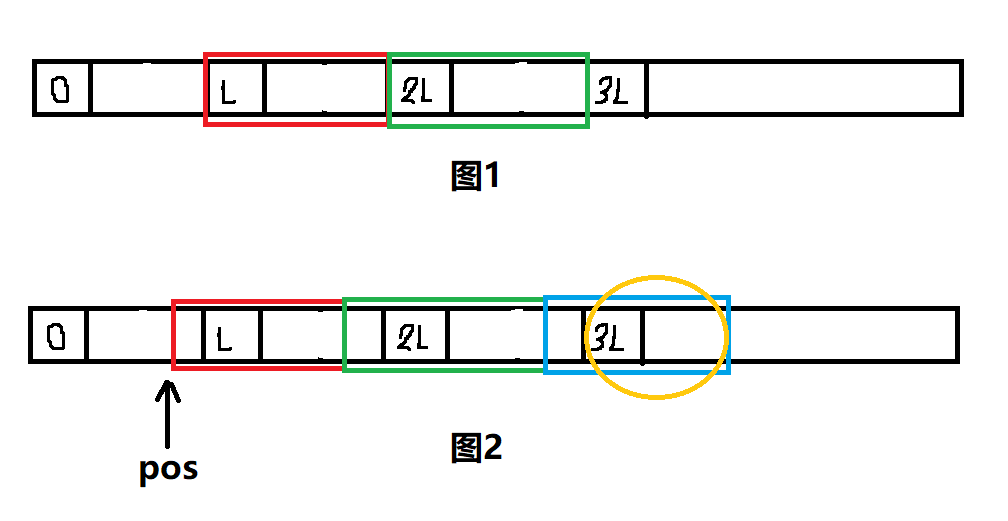
　　如果连续重复子串的首字符恰好在这些点上，那么连续重复子串出现的次数恰好是 \( \frac{lcp(L_1, L_2)}{L} + 1\)，(注：\(lcp\) 为 Longest Common Prefix 的简写），如图 1 所示；

　　否则，我们先计算出 \(lcp(L_1, L_2)\) 中 模 \( L\) 后余下的长度 \(L'\)，如图 2 中橙色圈里的片段，可以推测出连续重复子串真正的首字符位于 \( pos = L_1 - (L - L')\)，如果 \(0 \le pos\)，则连续重复子串出现的次数为：\( \frac{lcp(pos, pos+L)}{L} + 1\)。

　　记录出现的最多次数，即为答案。最长公共前缀的查询要用 RMQ 优化。

AC代码：

  1 #include <iostream>
  2 #include <cstdio>
  3 #include <algorithm>
  4 
  5 using namespace std;
  6 const int maxn = 50000 + 5, inf = 0x7fffffff;
  7 int len, tk;
  8 int Rank[maxn], tmp[maxn];
  9 int S[maxn];
 10 int sa[maxn], lcp[maxn];
 11 
 12 bool compare_sa(int i, int j) {
 13     if (Rank[i] != Rank[j])    return Rank[i] < Rank[j];
 14     else {
 15         int ri = i + tk <= len ? Rank[i + tk] : -1;
 16         int rj = j + tk <= len ? Rank[j + tk] : -1;
 17         return ri < rj;
 18     }
 19 }
 20 
 21 void construct_sa() {
 22     for (int i = 0; i <= len; i++) {
 23         sa[i] = i;
 24         Rank[i] = i < len ? S[i] : -1;
 25     }
 26 
 27     for (tk = 1; tk <= len; tk *= 2) {
 28         sort(sa, sa + len + 1, compare_sa);
 29         tmp[sa[0]] = 0;
 30         for (int i = 1; i <= len; i++) {
 31             tmp[sa[i]] = tmp[sa[i - 1]] + (compare_sa(sa[i - 1], sa[i]) ? 1 : 0);
 32         }
 33         for (int i = 0; i <= len; i++) {
 34             Rank[i] = tmp[i];
 35         }
 36     }
 37 }
 38 
 39 void construct_lcp() {
 40     int h = 0;
 41     lcp[0] = 0;
 42     for (int i = 0; i < len; i++) {
 43         int j = sa[Rank[i] - 1];
 44 
 45         if (h > 0)    h--;
 46         for (; j + h < len && i + h < len; h++) {
 47             if (S[j + h] != S[i + h])    break;
 48         }
 49         lcp[Rank[i] - 1] = h;
 50     }
 51 }
 52 
 53 int RMQ[maxn];
 54 int mm[maxn], best[20][maxn];
 55 void initRMQ(int n) {
 56     mm[0] = -1;
 57     for (int i = 1; i <= n; i++)
 58         mm[i] = ((i&(i - 1)) == 0) ? mm[i - 1] + 1 : mm[i - 1];
 59     for (int i = 1; i <= n; i++)    best[0][i] = i;
 60     for (int i = 1; i <= mm[n]; i++) {
 61         for (int j = 1; j + (1 << i) - 1 <= n; j++) {
 62             int a = best[i - 1][j];
 63             int b = best[i - 1][j + (1 << (i - 1))];
 64             if (RMQ[a] < RMQ[b])    best[i][j] = a;
 65             else
 66             {
 67                 best[i][j] = b;
 68             }
 69         }
 70     }
 71 }
 72 int askRMQ(int a, int b) {
 73     int t;
 74     t = mm[b - a + 1];
 75     b -= (1 << t) - 1;
 76     a = best[t][a];    b = best[t][b];
 77     return RMQ[a] < RMQ[b] ? a : b;
 78 }
 79 int find_lcp(int a, int b) {
 80     if (a>b) swap(a, b);
 81     return lcp[askRMQ(a, b - 1)];
 82 }
 83 int main()
 84 {
 85     char inp[5];
 86     int H;
 87     scanf("%d", &H);
 88     while (H--) {
 89         scanf("%d", &len);
 90         for (int i = 0; i<len; i++) {
 91             scanf("%s", inp);
 92             if (inp[0] == 'a') S[i] = 0;
 93             else    S[i] = 1;
 94         }
 95         construct_sa();
 96         construct_lcp();
 97         for (int i = 1; i <= len; i++)    RMQ[i] = lcp[i];
 98         initRMQ(len);
 99         int ans = 1;
100         for (int i = 1; i <= len; i++) {
101             int ret = 0;
102             for (int j = 0; j + i<len; j += i) {
103                 int r1 = Rank[j], r2 = Rank[j + i];
104                 int L = find_lcp(r1, r2);
105                 int temp = L / i + 1;
106                 int k = j - (i - L%i);
107                 if (k >= 0) {
108                     temp = find_lcp(Rank[k], Rank[k + i]) / i + 1;
109                 }
110                 ret = max(ret, temp);
111             }
112             ans = max(ans, ret);
113         }
114         printf("%d\n", ans);
115     }
116     return 0;
117 }

 

posted @ 2017-11-29 16:20  Blogggggg  阅读(225)  评论(0)  编辑  收藏  举报