HDU6035 Colorful Tree

题目链接：https://vjudge.net/problem/HDU-6035

题目大意：

　　多样例输入。

　　对于每一个样例，给出 n \((2 \le n \le 200000)\) 个结点的一棵树，各个节点都有各自的颜色 \(c_i  (1 \le c_i \le n)\)，树上任意两点之间的路径的权值为该路径经过的不同颜色的结点数，求树上所有两点路径的权值之和。

知识点：　　树、DFS

解题思路：

　　求树上所有的两点路径的权值之和，可以转化为求各个颜色在各条路径中的贡献值（即该颜色能够为树上的各条路径增加的权值的总和，也可以理解成是该颜色在多少条路径中出现）。但是，并没有非常好的方法可以直接求出这个总的贡献值，于是，我们可以反过来求：各个颜色在多少条路径中没有出现。


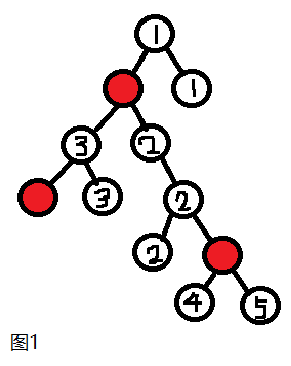
　　如图1所示，树上所有的红色结点将整棵树分成了 5 个联通块（笔者已用 1~5 标出），则这五个联通块里面的所有路径显然都没有经过红色结点。其实这些联通块也可以看成是一棵子树，对于一棵有 n 个结点的树，树上所有路径数为 \(\frac{n(n-1)}{2}\) 1

　　那么，我们所要求的答案其实就是\(\frac{NumberOfColors \times n \times (n-1)}{2}\) - 没有经过各个颜色的所有路径数

　　对于每一种颜色，没有经过该种颜色的路径可以分成两类：

　　1、从树根以下，到第一次接触颜色点之前的这一联通块的路径（如图1中的第1块）；

　　2、颜色点之间和颜色点以下直到叶子的联通块（如图1中的第2~5块）。

　　只要算出这两种路径的总数，即可求出答案，但此题的实现并不简单，请看代码及注释：

AC代码：

 1 #include <cstdio>
 2 #include <vector>
 3 #include <set>
 4 
 5 using namespace std;
 6 typedef long long ll;
 7 const int maxn=200000+5;
 8 
 9 int color[maxn];//记录各个结点的颜色
10 ll sum[maxn];//精髓所在
11 ll sizes[maxn];//记录各个结点以下的结点数
12 vector<int> tree[maxn];//记录树
13 set<int> col;
14 ll ans;
15 void find_size(int fa,int gfa){//找出各点的 sizes[i]
16     sizes[fa]=1;
17     for(int i=0;i<tree[fa].size();i++){
18         if(tree[fa][i]==gfa)    continue;
19         find_size(tree[fa][i],fa);
20         sizes[fa]+=sizes[tree[fa][i]];
21     }
22 }
23 void find_ans(int fa,int gfa){
24     ll tmp=0;
25     if(sum[color[fa]]!=0){  
26 //此处 sum[color[fa]] 记录的是目前已知的从各个分枝的第一个颜色为 color[fa] 的点到叶子的结点数，那么当最后求出这个值以后，上文提及的第一类路径的结点数即为 n-sum[i] 
27         tmp=sum[color[fa]];    
28         sum[color[fa]]=0;
29 /*      *****************       */
30     }
31     for(int i=0;i<tree[fa].size();i++){
32         if(tree[fa][i]==gfa)    continue;
33         find_ans(tree[fa][i],fa);
34 //此处sum[color[fa]]用于求从 tree[fa][i] 这个结点出发到下一个颜色为 color[fa] 或者叶子的联通块的结点数
35 //请注意上下两处划线处的代码
36         ans-=(sizes[tree[fa][i]]-sum[color[fa]])*(sizes[tree[fa][i]]-sum[color[fa]]-1)/2;
37         sum[color[fa]]=0;
38 /*      *****************       */
39     }sum[color[fa]]=sizes[fa]+tmp;
40 }
41 int main(){
42     int n,a,b;
43     int kase=1;
44     while(scanf("%d",&n)==1){
45         col.clear();
46         for(int i=1;i<=n;i++){
47             sum[i]=0;
48             tree[i].clear();
49         }
50         for(int i=1;i<=n;i++){
51             scanf("%d",&color[i]);
52             col.insert(color[i]);
53         }
54         ans=(ll)col.size()*n*(n-1)/2;
55         for(int i=1;i<n;i++){
56             scanf("%d%d",&a,&b);
57             tree[a].push_back(b);
58             tree[b].push_back(a);
59         }find_size(1,0);
60         find_ans(1,0);
61         set<int>::iterator pt=col.begin();
62         for(;pt!=col.end();pt++){
63             int cl=*pt;
64             ans-=(n-sum[cl])*(n-sum[cl]-1)/2;
65         }
66         printf("Case #%d: %lld\n",kase++,ans);
67     }return 0;
68 }

 

 

 

　　

　　

 

 

1、n(n-1)/2——此处的公式可能会挂，原因不明......

posted @ 2017-11-13 11:59  Blogggggg  阅读(255)  评论(0)  编辑  收藏  举报