XJOI 3864 农村连接城市

题意

平面上有 \(N\) 个城市和 \(M\) 个乡村，一开始没有任何的道路

为了改善这个局面，主席决定采取一些策略使得每个乡村都能连接到至少一个城市

当存在一个乡村与任何城市都没有联系时，执行如下操作

1. 随机挑选一个未联系的乡村 \(V\)

2. 选择离 \(V\) 最近（欧几里得距离）的一个已链接城市的乡村或者城市，如果有多个，满足条件的点，随机选择，假设选择的点为\(P\)

3. 在 \(V\) 与 \(P\) 之间 建设一条道路

求期望需要修建多长的道路能使得所有的乡村都能直接或者间接的连接到城市

输入格式

第一行输入两个整数\(n,m (1≤n≤50,1≤m≤50)\)

接下来一行输入 \(n\) 个整数 \(cityX[i]\) 表示第 \(i\) 个城市的 \(x\) 坐标

接下来一行输入 \(n\) 个整数 \(cityY[i]\) 表示第 \(i\) 个城市的 \(y\) 坐标

接下来一行输入 \(m\) 个整数 \(villageX[i]\) 表示第 \(i\) 个乡村的 \(x\) 坐标

接下来一行输入 \(m\) 个整数 \(villageY[i]\) 表示第 \(i\) 个乡村的 \(y\) 坐标

所有的点的坐标都是唯一的

所有坐标的值都在 \(0\) 到 \(1000000\) 以内

输出格式

输出一个浮点数，误差在 \(1e−9\) 之内

样例输入&输出

样例1

1 2
3
0
3 3
2 1

2.5

样例2

4 4
1 4 7 10
5 5 5 5
1 4 7 10
4 4 4 4

4.0

样例3

3 3
1 2 3
4 4 4
4 5 6
4 4 4

4.166666666666667

分析

对于某一个村庄 \(i\) ，我们把其他村庄按距离从近到远排序，再逐个枚举，加上期望。当枚举到第一个城市 \(k\) 时即退出循环，因为连接比第一个城市远的任何村庄或城市都无意义。

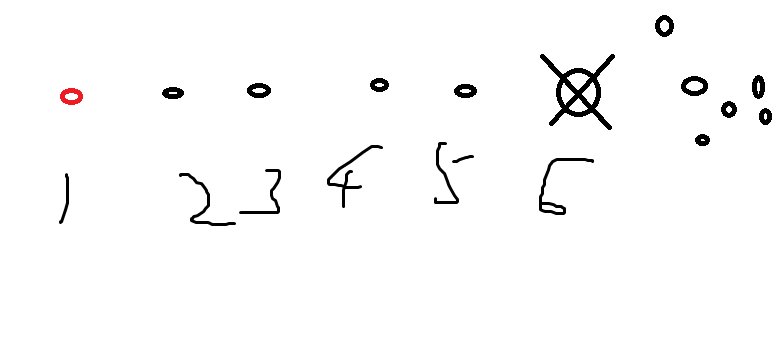
对于图中的村庄1,2,3,4,5，我们考虑它们连接城市6的先后顺序。

1. 2在1之前时连接的概率为 \(\frac{1}{2}\) ；

2. 2在1之后时，(1) 3在1之前的概率为 \(\frac{1}{3}\) （要保证2->1->3,3在最前面）， (2) 3在1之后再分类讨论4,5，然后求和即可。

我们发现，第 \(j\) 个村庄连上村庄 \(i\) 的概率为 \(\frac{1}{j(j+1)}\) 。最后还要加上村庄 \(i\) 直接连上枚举到的第一个城市 \(k\) 的概率（即 \(\frac{1}{k}\) ）

本题卡精度，double is recommended.

Code

#include<cstdio>
#include<algorithm>
#include<cmath>
#define maxn 52
#define sqr(x) ((x)*(x))
#define dis2(p,q) (sqr(p.x-q.x)+sqr(p.y-q.y))
#define dis(p,q) sqrt(sqr(p.x-q.x)+sqr(p.y-q.y))
using namespace std;
struct point{
    double x,y;
}c[maxn],v[maxn];
struct status{
    double x,y;
    bool isc; //是否是城市
}t[maxn<<1];
double sum;
int n,m,i,j;
bool cmp(const status& p,const status& q){
    return dis2(v[i],p)==dis2(v[i],q)?p.isc<q.isc:dis2(v[i],p)<dis2(v[i],q); //如果距离相同，则村庄优先；否则按距离从近到远排序
}
int main(){
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)scanf("%lf",&c[i].x);
    for(i=1;i<=n;i++)scanf("%lf",&c[i].y);
    for(i=1;i<=m;i++)scanf("%lf",&v[i].x);
    for(i=1;i<=m;i++)scanf("%lf",&v[i].y);
    for(i=1;i<=m;i++){ //枚举每一个村庄
        int cnt=0;
        for(j=1;j<=n;j++){
            t[++cnt].x=c[j].x,t[cnt].y=c[j].y,t[cnt].isc=1;
        }
        for(j=1;j<=m;j++){
            if(i==j){continue;} //排除掉自己连自己的情况
            t[++cnt].x=v[j].x,t[cnt].y=v[j].y,t[cnt].isc=0;
        }
        sort(t+1,t+n+m,cmp);
        for(j=1;j<n+m;j++){
            if(t[j].isc){
                sum+=dis(v[i],t[j])/j; //加上连接城市的期望
                break;
            }
            sum+=dis(v[i],t[j])/(j*(j+1)); //加上连接村庄的期望
        }
    }
    printf("%.10lf",sum); //答案为所有村庄期望之和
    return 0;
}