后缀数组
教程
论文(下面的题目论文里基本上都有)
Part 1
A. 不重叠最长重复子串
直接求 \(\max{height[i]}\) 即可
B. 重叠 \(k\) 次最长重复子串
二分答案子串的长度,把题目变成判定性问题,按照 \(height[i]>=mid\) 把 \(height\) 数组分成若干块,最后统计出现次数是否 \(\le k\) 。
C. 一个字符串中不同子串个数
对于每个后缀它的贡献是 \(n-sa[i]+1-height[i]\)
D. 一个字符串的最长回文子串
将该字符串reverse后接在原字符串后面,用'$'连接,再求最长公共子串。(见下)
E. 连续重复子串
\(n\le 10^6\)
//SA
for(int i=1;i<=n;i++)if(n%i==0&&lcp(1,i+1)==n-i){printf("%d\n",n/i);break;}
\(O(n\log n)\) ,不能通过本题
//kmp
printf("%d\n",n%(n-nxt[n])==0?n/(n-nxt[n]):1);
\(O(n)\) ,可以通过本题
F. 一个串重复次数最多的连续重复子串
for(int i=1;i<=n;i++){
for(int j=1;j<=n-i;j+=i){
int pos=j-i+modulo(j+i+lcp(j,j+i)-1,i);
if(pos<=0)pos=1;
int tmp=lcp(pos,pos+i)/i+1;
if(tmp>ans)ans=tmp,len[cnt=1]=i;
else if(tmp==ans&&len[cnt]!=i)len[++cnt]=i;
}
}
bool flag=0;
for(int i=1;i<=n&&!flag;i++){
for(int j=1;j<=cnt&&sa[i]+len[j]<=n&&!flag;j++){
if(lcp(sa[i],sa[i]+len[j])>=(ans-1)*len[j]){
printf("Case %d: ",++T);
for(int l=sa[i];l<=sa[i]+len[j]*ans-1;l++)putchar(s[l]);
puts("");
flag=1;
}
}
}
好dark的算法,复杂度证不来,反正过了就行
G. 最长公共子串
首先将两个字符串拼成一个,如果 \(sa[i-1]\) 和 \(sa[i]\) 分局两侧就更新答案。
H. 两个字符串的长度 \(≥ k\) 的最长公共子串个数
重要
把 \(height\) 数组按 \(height[i]>=k\) 分成若干块,然后用单调栈扫。\(cnt[i]\) 维护的是在 \(i\) 之前最靠近 \(i\) 的一个大于等于 \(height[i]\) 的连通块。
e.g.
假设我们现在的height数组是长这样的:
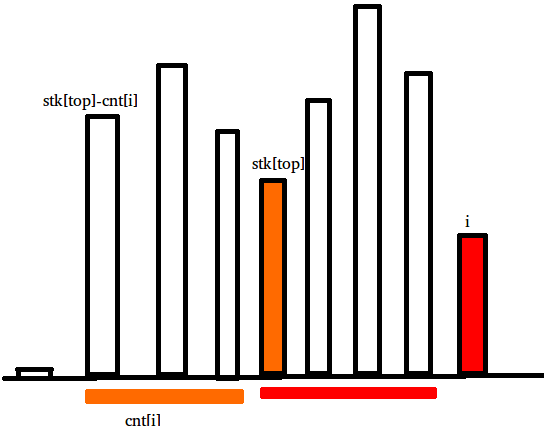
扫 \(i\) 之前的栈:1 5 6 8
现在第9个元素将把5,6,8弹出栈,图片上是弹出5的情况
当弹出完成时,就只剩下 \(i-cnt[i]\) 到 \(i-1\) 对 \(i\) 的贡献了。
Code
int main(){
while(scanf("%d",&k),k){
scanf("%s",s+1);
len=strlen(s+1);
s[len+1]='!';
scanf("%s",s+len+2);
n=strlen(s+1);
sufsort();
geth();
int top=0;
long long sum=0,ans=0;
for(int i=1;i<=n;i++){
if(height[i]>=k){
int tot=0;
if(sa[i-1]<=len)tot++,sum+=(long long)height[i]-k+1;
while(top&&height[i]<=height[stk[top]]){
tot+=cnt[stk[top]];
sum-=(long long)cnt[stk[top]]*(height[stk[top]]-height[i]);
top--;
}
cnt[i]=tot;
stk[++top]=i;
if(sa[i]>len)ans+=sum;
}
else top=sum=0;
}
top=sum=0;
for(int i=1;i<=n;i++){
if(height[i]>=k){
int tot=0;
if(sa[i-1]>len)tot++,sum+=(long long)height[i]-k+1;
while(top&&height[i]<=height[stk[top]]){
tot+=cnt[stk[top]];
sum-=(long long)cnt[stk[top]]*(height[stk[top]]-height[i]);
top--;
}
cnt[i]=tot;
stk[++top]=i;
if(sa[i]<=len)ans+=sum;
}
else top=sum=0;
}
printf("%lld\n",ans);
}
return 0;
}
I. 有 \(n\) 个字符串,出现在至少 \(n/2\) 个字符串中的最长子串
\(n\le 100,length\le 1000\)
先二分长度,再分块,再用一个bool[]在哪几个字符串出现过。
J. 求 \(n\) 个字符串中在每个字符串出现至少两次的最长子串
\(n\le 10,length\le 10000\)
二分长度,开一个bool[],统计
K. 求 \(\sum_{1\le i<j\le n}lcp(Suffix_i,Suffix_j)\)
he
单调栈优化dp
Code
int main(){
scanf("%s",s+1);
n=strlen(s+1);
sufsort();
geth();
int top=0;
long long ans=0;
for(int i=1;i<=n;i++){
while(top&&height[i]<=height[stk[top]])top--;
if(top)dp[i]=(long long)(i-stk[top])*height[i]+dp[stk[top]];
ans+=dp[i];
stk[++top]=i;
}
printf("%lld\n",(long long)(n-1)*n*(n+1)/2-2*ans);
return 0;
}
Part 2
A
给你26个英文字母是好的还是坏的,现在给你一个长度 \(\le 1500\) 的字符串,问至多存在 \(k\) 个坏字母的子串有多少个。
解
用后缀数组或者其它方法 \(n^2\) 暴力搞一下就行了
D
有三个字符串。你需要确定对于每个 \(l (1 ≤ l ≤ \min(|s_1|, |s_2|, |s_3|)\) 有多少三元组 \((i_1, i_2, i_3)\) ,满足三个 \(s_k[i_k... i_{k + l - 1}] (k = 1, 2, 3)\) 都相等。膜 \(10^9+7\) 。
解
cmp(int x,int y){return height[x]>height[y];}
main(){
for(int i=1;i<=n;i++)a[i]=i,f[i]=i;
for(int i=1;i<=len[1];i++)sum[i][1]=1;
for(int i=len[1]+2;i<=len[2];i++)sum[i][2]=1;
for(int i=len[2]+2;i<=len[3];i++)sum[i][3]=1;
sort(a+1,a+n+1,cmp);
long long ans=0;
for(int i=k,j=1;i>=1;i--){
for(;j<=n&&height[a[j]]>=i;j++){
int l=find(sa[a[j]-1]),r=find(sa[a[j]]);
ans=((ans-(long long)sum[l][1]*sum[l][2]*sum[l][3]%mod+mod)%mod-(long long)sum[r][1]*sum[r][2]*sum[r][3]%mod+mod)%mod;
sum[l][1]+=sum[r][1],sum[l][2]+=sum[r][2],sum[l][3]+=sum[r][3];
ans=(ans+(long long)sum[l][1]*sum[l][2]*sum[l][3]%mod)%mod;
f[r]=l;
}
ANS[i]=ans;
}
ios::sync_with_stdio(0);
for(int i=1;i<=k;i++)cout<<ANS[i]<<' ';
}
E
有一个字符串和 \(q\) 组询问,每组询问有两个数组 \(a_1, a_2, \dots, a_k\) 、 \(b_1, b_2, \dots, b_l\) ,计算 \(\sum\limits_{i = 1}^{i = k} \sum\limits_{j = 1}^{j = l}{\text{LCP}(s[a_i \dots n], s[b_j \dots n])}\) 。
解
和上面的H题大同小异
bool cmp(const SS& x,const SS& y){return rnk[x.a]==rnk[y.a]?x.mo<y.mo:rnk[x.a]<rnk[y.a];}
int main(){
for(int i=2;i<maxn;i++)lg[i]=lg[i-1]+((1<<(lg[i-1]+1))==i);
int Q;
scanf("%d%d%s",&n,&Q,s+1);
sufsort();
geth();
initst();
while(Q--){
int cnta,cntb,top=0;
long long ans=0,sum=0;
scanf("%d%d",&cnta,&cntb);
for(int i=1;i<=cnta;i++){int x;scanf("%d",&x);ss[i]=SS(x,0);}
for(int i=1;i<=cntb;i++){int x;scanf("%d",&x);ss[i+cnta]=SS(x,1);}
sort(ss+1,ss+cnta+cntb+1,cmp);
for(int i=1;i<=cnta+cntb;i++){
int tot=0;
if(!ss[i-1].mo)tot++,sum+=lcp(ss[i].a,ss[i-1].a);
while(top&&lcp(ss[i].a,ss[i-1].a)<=lcp(ss[stk[top]].a,ss[stk[top]-1].a)){
tot+=cnt[stk[top]];
sum-=(long long)cnt[stk[top]]*(lcp(ss[stk[top]].a,ss[stk[top]-1].a)-lcp(ss[i].a,ss[i-1].a));
top--;
}
cnt[i]=tot;
stk[++top]=i;
if(ss[i].mo)ans+=sum;
}
top=sum=0;
for(int i=1;i<=cnta+cntb;i++){
int tot=0;
if(ss[i-1].mo)tot++,sum+=lcp(ss[i].a,ss[i-1].a);
while(top&&lcp(ss[i].a,ss[i-1].a)<=lcp(ss[stk[top]].a,ss[stk[top]-1].a)){
tot+=cnt[stk[top]];
sum-=(long long)cnt[stk[top]]*(lcp(ss[stk[top]].a,ss[stk[top]-1].a)-lcp(ss[i].a,ss[i-1].a));
top--;
}
cnt[i]=tot;
stk[++top]=i;
if(!ss[i].mo)ans+=sum;
}
printf("%lld\n",ans);
}
return 0;
}
F
记 \(a\) 为字符串的一个子串, \(f(a)\) 为 \(a\) 在字符串中出现的次数,但是 \(a\) 不能以字符串中的某些位置结尾,求最大的 \(|a|*f(a)\) 。
解
把字符串反转一下,问题变为不能以字符串中的某些位置开头,然后就变成了单调栈问题。
int main(){
scanf("%d%s%s",&n,s+1,b+1);
reverse(s+1,s+n+1),reverse(b+1,b+n+1);
sufsort();
geth();
long long ans=0;
int top=0;
for(int i=1;i<=n;i++){
if(b[sa[i-1]]=='0')cnt[i]++;
while(top&&height[i]<=height[stk[top]]){
cnt[i]+=cnt[stk[top]];
ans=max(ans,(long long)cnt[i]*height[stk[top]]);
top--;
}
stk[++top]=i;
}
if(b[sa[n]]=='0')cnt[n+1]++;
while(top){
cnt[n+1]+=cnt[stk[top]];
ans=max(ans,(long long)cnt[n+1]*height[stk[top]]);
top--;
}
for(int i=1;i<=n;i++)if(b[i]=='0'){ans=max(ans,(long long)n-i+1);break;}
cout<<ans<<endl;
return 0;
}
B
解
struct data{
int val,len;
data():val(0),len(0){}
data(int _v,int _l):val(_v),len(_l){}
friend const data& max(const data& x,const data& y){return (x.val==y.val?x.len<y.len:x.val>y.val)?x:y;}
};
struct node{data a,z;int mi;}t[maxn<<2];
void pushup(int p){t[p].a=max(t[p<<1].a,t[p<<1|1].a),t[p].mi=min(t[p<<1].mi,t[p<<1|1].mi);}
void pushdown(int p,int l,int r){
if(l==r)return;
if(t[p].z.val||t[p].z.len){
t[p<<1].a=max(t[p<<1].a,t[p].z),t[p<<1|1].a=max(t[p<<1|1].a,t[p].z);
t[p<<1].z=max(t[p<<1].z,t[p].z),t[p<<1|1].z=max(t[p<<1|1].z,t[p].z);
t[p].z=data();
}
}
void build(int p,int l,int r){
t[p].mi=INF;
if(l==r)return;
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
}
void change(int p,int l,int r,int seg_l,int seg_r,const data& k){
pushdown(p,l,r);
if(seg_l<=l&&r<=seg_r){t[p].a=max(t[p].a,k);t[p].z=k;return;}
int mid=(l+r)>>1;
if(seg_l<=mid)change(p<<1,l,mid,seg_l,seg_r,k);
if(seg_r>mid)change(p<<1|1,mid+1,r,seg_l,seg_r,k);
pushup(p);
}
void change(int p,int l,int r,int pos,int k){
pushdown(p,l,r);
if(l==r){t[p].mi=k;return;}
int mid=(l+r)>>1;
if(pos<=mid)change(p<<1,l,mid,pos,k);
else change(p<<1|1,mid+1,r,pos,k);
pushup(p);
}
const data& query(int p,int l,int r,int pos){
pushdown(p,l,r);
if(l==r)return t[p].a;
int mid=(l+r)>>1;
if(pos<=mid)return query(p<<1,l,mid,pos);
else return query(p<<1|1,mid+1,r,pos);
}
int query(int p,int l,int r,int seg_l,int seg_r){
pushdown(p,l,r);
if(seg_l<=l&&r<=seg_r)return t[p].mi;
int mid=(l+r)>>1,ret=INF;
if(seg_l<=mid)ret=min(ret,query(p<<1,l,mid,seg_l,seg_r));
if(seg_r>mid)ret=min(ret,query(p<<1|1,mid+1,r,seg_l,seg_r));
return ret;
}
pair<int,int> binary_search(int pos,int len){
int L,R,l=1,r=pos,mid;
while(l<=r){
mid=(l+r)>>1;
if(lcp(mid,pos)>=len)L=mid,r=mid-1;
else l=mid+1;
}
l=pos,r=n;
while(l<=r){
mid=(l+r)>>1;
if(lcp(pos,mid)>=len)R=mid,l=mid+1;
else r=mid-1;
}
return make_pair(L,R);
}
int main(){
scanf("%d%s",&n,s+1);
sufsort(),geth(),initst();
build(1,1,n);
pair<int,int> tmp;
int ans=0;
for(int i=n;i>=1;i--){
int val,len,l,r;
data x=query(1,1,n,rnk[i]);
if(x.val==0)val=len=1;
else{
val=x.val+1;
tmp=binary_search(rnk[i],x.len),l=tmp.first,r=tmp.second;
len=query(1,1,n,l,r)+x.len-i;
}
change(1,1,n,rnk[i],i);
tmp=binary_search(rnk[i],len),l=tmp.first,r=tmp.second;
change(1,1,n,l,r,data(val,len));
ans=max(ans,val);
}
printf("%d\n",ans);
return 0;
}
C
解
bool check(int i,int length){
int L=i,R=i,l=1,r=i-1,mid;
while(l<=r){
mid=(l+r)>>1;
if(lcp(mid,i)>=length)L=mid,r=mid-1;//,o(mid);
else l=mid+1;
}
l=i+1,r=n;
while(l<=r){
mid=(l+r)>>1;
if(lcp(i,mid)>=length)R=mid,l=mid+1;
else r=mid-1;
}
return lef[R]>=L;
}
int main(){
scanf("%d%d",&N,&k);
if(k>N){for(int i=1;i<=N;i++)printf("0 ");return 0;}
len[0]=-1;
for(int i=1;i<=N;i++){
if(i>1)s[len[i-1]+1]=i-100001;
scanf("%s",str+1);
len[i]=len[i-1]+1+strlen(str+1);
for(int j=len[i-1]+2;j<=len[i];j++)s[j]=str[j-len[i-1]-1],p[j]=i;
}
n=len[N];
sufsort();
geth();
initst();
for(int i=1;i<=n;i++)buc[i]=0;
for(int i=N,j=0,tot=buc[p[sa[i]]]=1;i<=n;i++,tot+=!buc[p[sa[i]]],buc[p[sa[i]]]++){
for(;j<=i&&tot>=k;buc[p[sa[j]]]--,tot-=!buc[p[sa[j]]],j++);
if(j)j--,tot+=!buc[p[sa[j]]],buc[p[sa[j]]]++;
lef[i]=j;
}
long long ans=0;
ios::sync_with_stdio(0);
for(int i=1,length=0;i<=n;i++){
if(p[i]==0)cout<<ans<<' ',ans=0,length=0;
else{
if(length)length--;
for(;i+length-1<=len[p[i]]&&check(rnk[i],length);length++);
length--;
ans+=length;
}
}
cout<<ans<<endl;
return 0;
}


