Codeforces 500

500 C

题意

给你一个栈，栈中有若干个带权的元素，开始时有 \(n\) 个元素 \(1-n\) ，你可以进行以下操作：

• 将元素 \(x(x\in [1,n])\) 取出栈，花费为在 \(x\) 上面所有元素的权值和，再将 \(x\) 放在栈顶

现在给你一个 \(x\) 序列，问怎么安排初始的栈使花费最小。
\((n\le 10^5)\)

Examples

input
3 5
1 2 3
1 3 2 3 1
output
12

解

考虑贪心，将先取的书放在上面。

500 D

题意

有一棵树，有边权，现在随机选择一个三元组 \((x,y,z)\) 花费为 \(dis(x,y)+dis(y,z)+dis(z,x)\) ，求三元组花费的期望。
\((n\le 10^5)\)

Examples

input
3
2 3 5
1 3 3
5
1 4
2 2
1 2
2 1
1 1
output
14.0000000000
12.0000000000
8.0000000000
6.0000000000
4.0000000000
input
6
1 5 3
5 3 2
6 1 7
1 4 4
5 2 3
5
1 2
2 1
3 5
4 1
5 2
output
19.6000000000
18.6000000000
16.6000000000
13.6000000000
12.6000000000

解

对于这种题最好的方法是找规律
通过一番寻找，我们发现每条边对答案的贡献为 \(\frac{边的两个端点的两颗子树大小的乘积*(n-2)}{C^{n}_{3}}\)
注意这道题某些中间过程能让long long都炸掉，开double

500 E

题意

在坐标轴上有 \(n\) 个多米诺骨牌，原理如图

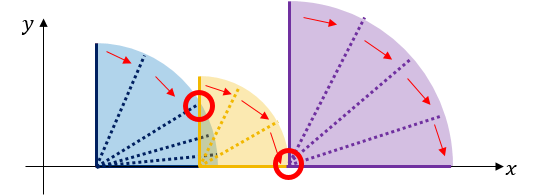
现在你可以给每一个骨牌的长度 \(+1\)
现在有 \(m\) 组询问，问从 \(x\) 到 \(y\) 最少需要 \(+1\) 多少次
\((n,m\le 10^5)\)

Examples

input
6
1 5
3 3
4 4
9 2
10 1
12 1
4
1 2
2 4
2 5
2 6
output
0
1
1
2

解

把多米诺骨牌平摊在 \(x\) 轴上，然后把相交的骨牌连在一个联通块里，从后往前扫，用单调栈维护。询问需离线。

Code

#include<bits/stdc++.h>
#define maxn 200003
#define INF 1050000000
using namespace std;
int n,Q,top,stk[maxn],f[maxn],sum[maxn],L[maxn],R[maxn],ans[maxn];
struct data{int x,len;}a[maxn];
struct QQ{int l,r,num;bool operator <(const QQ& x)const{return l<x.l;}}q[maxn];
int find(int x){return x!=f[x]?f[x]=find(f[x]):f[x];}
void Union(int x,int y){int fx=find(x),fy=find(y);if(fx!=fy)f[fx]=fy;}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d%d",&a[i].x,&a[i].len);
	scanf("%d",&Q);
	for(int i=1;i<=Q;i++)scanf("%d%d",&q[i].l,&q[i].r),q[i].num=i;
	sort(q+1,q+Q+1);
	for(int i=1;i<=n+1;i++)f[i]=i;
	L[n+1]=a[n].x+a[n].len;
	for(int i=n,j=Q;i>=1;i--){
		while(top&&a[i].x+a[i].len>=a[stk[top]].x+a[stk[top]].len)Union(i,stk[top]),top--;
		if(top&&a[i].x+a[i].len>=a[stk[top]].x)Union(i,stk[top]);
		int now=find(i),nxt=find(find(i)+1);
		if(now==i){
			R[now]=a[i].x+a[i].len;
			sum[now]=sum[nxt]+L[nxt]-R[now];
		}
		else{
			R[now]=max(R[now],a[i].x+a[i].len);
			sum[now]=min(sum[now],sum[nxt]+L[nxt]-R[now]);
		}
		L[now]=a[i].x;
		for(now=find(q[j].l);j>=1&&q[j].l>=i;j--){
			nxt=find(q[j].r);
			ans[q[j].num]=sum[now]-sum[nxt];
		}
		stk[++top]=i;
	}
	for(int i=1;i<=Q;i++)printf("%d\n",ans[i]);
	return 0;
}