Codeforces 593

593 B

题意

给你 \(n\) 条直线（没有与y轴平行的直线），问有没有一个交点在 \((X_1,X_2)\) 内。( \(2 ≤ n ≤ 100000\) )

Examples

Input
4
1 2
1 2
1 0
0 1
0 2
Output
NO
Input
2
1 3
1 0
-1 3
Output
YES
Input
2
1 3
1 0
0 2
Output
YES
Input
2
1 3
1 0
0 3
Output
NO

解

以 \(f(X_1)\) 为第一关键字， \(f(X_2)\) 为第二关键字排序，如果存在相邻的两条直线，第一条的左端点大于第二条的左端点，第一条的右端点小于第二条的右端点，就Yes

Code

#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
typedef pair<long long,long long> P;
P a[maxn];
long long n,X1,X2;
int main(){
    scanf("%lld%lld%lld",&n,&X1,&X2);
    for(int i=1;i<=n;i++){
        long long k,b;
        scanf("%lld%lld",&k,&b);
        a[i]=P(k*X1+b,k*X2+b);
    }
    sort(a+1,a+n+1);
    bool flag=0;
    for(int i=2;i<=n;i++){
        if(a[i].second<a[i-1].second){flag=1;break;}
    }
    puts(flag?"YES":"NO");
    return 0;
}

593 C

题意

平面上有 \(n\) 个圆，现在请你构造两个函数 \(f(t),g(t)\) ，使得当 \(t\in Z∩[1,50]\) 时， \((x=f(t),y=g(t))\) 的 \(51\) 个点与所有的圆相交。( \(1\le n\le 50\) )

Examples

Input
3
0 10 4
10 0 4
20 10 4
Output
t
abs((t-10))

解

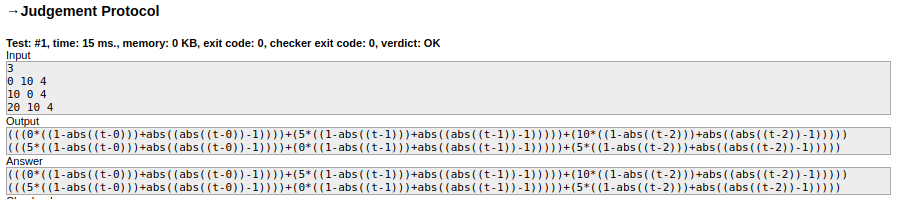
观察~~样例标答的~~函数，发现 \(1-|x-a|+||x-a|-1|\) 是一个类似开关的函数。 \(f(x)=1-|x-10|+||x-10|-1|\) 的图像如下：

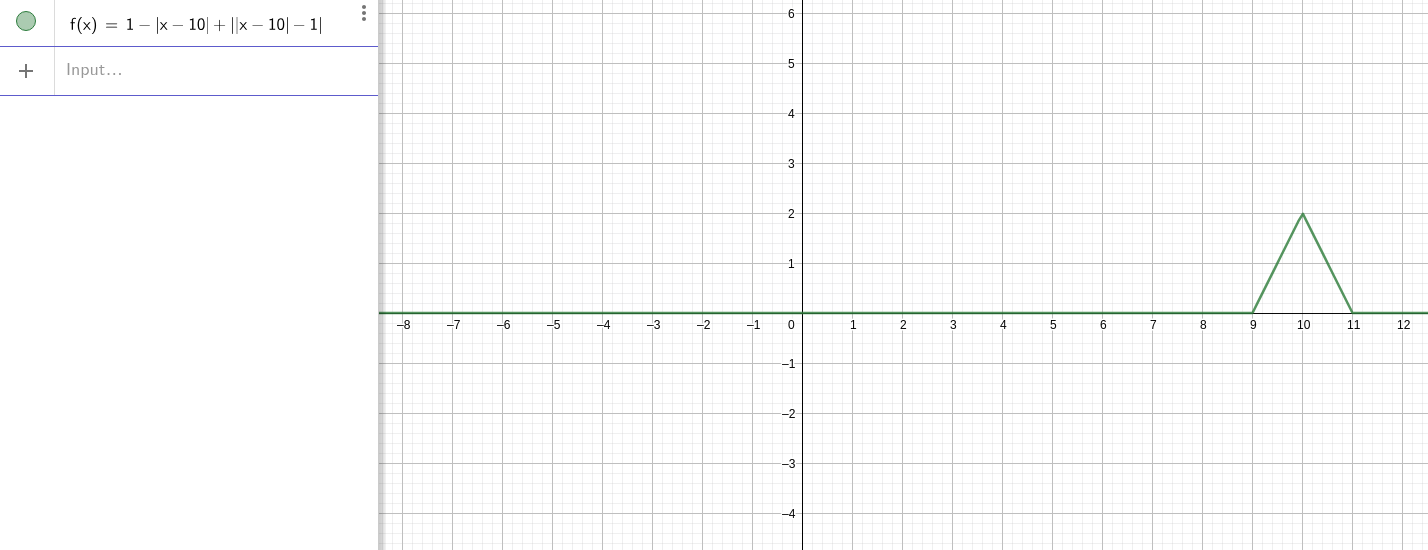
因此，我们只需对每一个圆的x和y坐标加上一个这种形式即可。

Code

#include<bits/stdc++.h>
#define maxn 53
using namespace std;
string s,t;
char tmp[20];
string itostr(int x){
    sprintf(tmp,"%d",x);
    return tmp;
}
int main(){
    int n,x,y,tmp;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>x>>y>>tmp;
        s+="("+itostr(x/2)+"*((1-abs((t-"+itostr(i)+")))+abs((abs((t-"+itostr(i)+"))-1))))";
        t+="("+itostr(y/2)+"*((1-abs((t-"+itostr(i)+")))+abs((abs((t-"+itostr(i)+"))-1))))";
        if(i)s+=')',t+=')';
        s+='+',t+='+';
    }
    s.erase(s.end()-1),t.erase(t.end()-1);
    s=string(n-1,'(')+s,t=string(n-1,'(')+t;
    cout<<s<<endl<<t<<endl;
    return 0;
}

593 D

题意

给你一棵树，有边权。现在有两种操作：

\(a_i\;b_i\;y_i\) ：在从点 \(a_i\) 到点 \(b_i\) 的路径中，每经过一条边，将 \(y_i\) 变为 \(floor(\frac{y_i}{w})\) ， \(w\) 为边权，要求输出 \(y_i\) 最终的值；
\(p_i\;c_i\) ：将第 \(p_i\) 条边的权值改为 \(c_i\) ， \(c_i\) 小于该边当前的权值。

( \(2 ≤ n ≤ 200000, 1 ≤ m ≤ 200000, \text{all numbers} \le 10^{18}\) )

Examples

Input
6 6
1 2 1
1 3 7
1 4 4
2 5 5
2 6 2
1 4 6 17
2 3 2
1 4 6 17
1 5 5 20
2 4 1
1 5 1 3
Output
2
4
20
3
Input
5 4
1 2 7
1 3 3
3 4 2
3 5 5
1 4 2 100
1 5 4 1
2 2 2
1 1 3 4
Output
2
0
2

解 1

树链剖分。
将每条边的边权转移到它的儿子上。
线段树上维护区间的乘积，如果乘积超过 \(10^{18}\) ，就存 \(-1\) 。
至于怎么判断两个long long的乘积是否大于 \(10^{18}\) ：\(a*b>10^{18} ⇔ a>10^{18}/b\)

解 2

充分利用“ \(c_i\) 小于该边当前的权值”“所有的数 \(\le 10^{18}\) ”这些条件。
如果一条边边权为 \(1\) ，那么把它的两个端点缩掉
所以：
对于操作1，暴力往上跳，最多只需要跳 \(\log\) 次
对于操作2，多加一个缩点操作
~~快得飞起~~

Code 2

#include<bits/stdc++.h>
#define maxn 200002
#define INF 1000000000000000001ll
using namespace std;
typedef long long D;
struct edge{
    D from,to,next,w;
}e[maxn<<1];
D head[maxn],cnte;
void add(D u,D v,D w){
    e[++cnte].to=v;
    e[cnte].from=u;
    e[cnte].w=w;
    e[cnte].next=head[u];
    head[u]=cnte;
}
D f[maxn];
D find(D x){
    if(x!=f[x])f[x]=find(f[x]);
    return f[x];
}
void Union(D x,D y){
    D fx=find(x),fy=find(y);
    if(fx!=fy)f[fx]=fy;
}
D n,dep[maxn],fa[maxn],num[maxn];
void initdep(D u,D last,D depth){
    dep[u]=depth;
    for(D i=head[u];~i;i=e[i].next){
        D v=e[i].to;
        if(v==last)continue;
        initdep(v,u,depth+1);
        fa[v]=u;
        num[v]=i;
    }
}
void initbelong(D u,D last){
    for(D i=head[u];~i;i=e[i].next){
        D v=e[i].to;
        if(v==last)continue;
        if(e[i].w==1)Union(v,u),dep[v]=dep[find(v)];
        initbelong(v,u);
    }
}
D query(D x,D y){
    D ans=1;
    while((x=find(x))!=(y=find(y))){
        if(dep[x]<dep[y])swap(x,y);
        if(ans>1000000000000000000ll/e[num[x]].w)return INF;
        else ans*=e[num[x]].w;
        x=fa[x];
    }
    return ans;
}
int main(){
    D Q;
    scanf("%lld%lld",&n,&Q);
    for(D i=1;i<=n;i++)head[i]=-1;
    cnte=-1;
    for(D i=1;i<n;i++){
        D u,v,w;
        scanf("%lld%lld%lld",&u,&v,&w);
        add(u,v,w);
        add(v,u,w);
    }
    initdep(1,0,1);
    for(D i=1;i<=n;i++)f[i]=i;
    initbelong(1,0);
    while(Q--){
        D mo,x,y;
        scanf("%lld%lld%lld",&mo,&x,&y);
        if(mo==2){
            int pos=x*2-2;
            if(y==1&&e[pos].w!=1){
                int uu=find(e[pos].from),vv=find(e[pos].to);
                int u=(dep[uu]<dep[vv]?uu:vv),v=(dep[uu]>dep[vv]?uu:vv);
                Union(v,u);
                dep[v]=dep[find(v)];
            }
            e[pos].w=e[pos+1].w=y;
        }
        else{
            D z;
            scanf("%lld",&z);
            D ans=query(x,y);
            printf("%lld\n",ans==INF?0:z/ans);
        }
    }
    return 0;
}

593 E

题意

一张表格，一个人最初在点 \((1,1)\)
这个人每次可以往上下左右走一格，也可以停留在原地
在某个时刻，有 \(3\) 种事件可能会发生：

他会收到邀请到某个点（此时这个点上保证没有猫），此时他必须赶到那个点
一只猫出现在某个点，此时他不能经过那个点
一只猫从某个点消失，此时他又能经过那个点

求 \(1\) 中他能赶到那个点的方案数
膜 \(10^9+7\)

Examples

Input
1 3 3
2 1 2 3
3 1 2 5
1 1 1 7
Output
5
Input
3 3 3
2 2 2 2
1 3 3 5
1 3 3 7
Output
2
42
Input
4 5 5
2 2 5 3
2 2 4 6
3 2 4 9
1 4 4 13
1 4 4 15
Output
490902
10598759

解

矩阵快速幂。
把dp的二维数组压成一维。
转移方程：
\(dp[gt(i,j)]=dp[gt(i-1,j)]+dp[gt(i+1,j)]+dp[gt(i,j-1)]+dp[gt(i,j+1)]+dp[gt(i,j)]\) （ \((i,j)\) 无猫）
\(dp[gt(i,j)]=0\) （ \((i,j)\) 有猫）

Code

#include<bits/stdc++.h>
#define maxn 22
#define mod 1000000007
using namespace std;
long long L(long long x){return x>=mod?x%mod:x;}
struct matrix{
    int N,M;
    long long a[maxn][maxn];
    matrix(){}
    matrix(const matrix& A){
        N=A.N,M=A.M;
        for(int i=1;i<=N;i++)for(int j=1;j<=M;j++)a[i][j]=A.a[i][j];
    }
    matrix& operator =(const matrix& A){
        N=A.N,M=A.M;
        for(int i=1;i<=N;i++)for(int j=1;j<=M;j++)a[i][j]=A.a[i][j];
        return *this;
    }
    void init(int _N,int _M){
        N=_N,M=_M;
        for(int i=1;i<=N;i++)for(int j=1;j<=M;j++)a[i][j]=0;
    }
    matrix operator *(const matrix& A)const{
        matrix ret;
        ret.init(N,A.M);
        for(int i=1;i<=N;i++)for(int j=1;j<=A.M;j++)for(int k=1;k<=M;k++)ret.a[i][j]=L(ret.a[i][j]+L(a[i][k]*A.a[k][j]));
        return ret;
    }
    matrix operator ^(long long x)const{
        matrix ret,A(*this);
        ret.init(N,N);
        for(int i=1;i<=N;i++)ret.a[i][i]=1;
        while(x){
            if(x&1)ret=ret*A;
            A=A*A;
            x>>=1;
        }
        return ret;
    }
};

int n,m,q,a[10002][4];
matrix A,DP;
int gt(int i,int j){return (i-1)*m+j;}
int main(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=q;i++){
        for(int j=0;j<4;j++)scanf("%d",&a[i][j]);
        if(a[i][0]==2)a[i][3]--;
    }
    a[0][3]=1;
    A.init(n*m,1);
    A.a[gt(1,1)][1]=1;
    DP.init(n*m,n*m);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(i>1)DP.a[gt(i,j)][gt(i-1,j)]=1;
            if(i<n)DP.a[gt(i,j)][gt(i+1,j)]=1;
            if(j>1)DP.a[gt(i,j)][gt(i,j-1)]=1;
            if(j<m)DP.a[gt(i,j)][gt(i,j+1)]=1;
            DP.a[gt(i,j)][gt(i,j)]=1;
        }
    }
    for(int qq=1;qq<=q;qq++){
        A=(DP^(a[qq][3]-a[qq-1][3]))*A;
        int i=a[qq][1],j=a[qq][2];
        if(a[qq][0]==1){
            printf("%lld\n",A.a[gt(i,j)][1]);
        }
        if(a[qq][0]==2){
            if(i>1)DP.a[gt(i,j)][gt(i-1,j)]=0;
            if(i<n)DP.a[gt(i,j)][gt(i+1,j)]=0;
            if(j>1)DP.a[gt(i,j)][gt(i,j-1)]=0;
            if(j<m)DP.a[gt(i,j)][gt(i,j+1)]=0;
            DP.a[gt(i,j)][gt(i,j)]=0;
        }
        if(a[qq][0]==3){
            if(i>1)DP.a[gt(i,j)][gt(i-1,j)]=1;
            if(i<n)DP.a[gt(i,j)][gt(i+1,j)]=1;
            if(j>1)DP.a[gt(i,j)][gt(i,j-1)]=1;
            if(j<m)DP.a[gt(i,j)][gt(i,j+1)]=1;
            DP.a[gt(i,j)][gt(i,j)]=1;
        }
    }
    return 0;
}

posted @ 2019-02-17 16:23 chc_1234567890 阅读(284) 评论(0) 编辑收藏举报

刷新页面返回顶部

chc_1234567890

Codeforces 593

593 B

题意

Examples

解

Code

593 C

题意

Examples

解

Code

593 D

题意

Examples

解 1

解 2

Code 2

593 E

题意

Examples

解

Code

公告