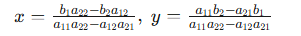Cramer法则-我的数学观

一、Cramer法则的历史背景与数学洞察

18世纪中叶，数学家Gabriel Cramer在研究n元线性方程组时，发现了一个惊人的规律：对于形如的线性方程组（其中A为系数矩阵），其解的每个分量均可表示为两个特殊组合的比值。

具体而言，分母为系数矩阵的行列式，而分子是将系数矩阵第i列替换为常数项b后构成的新行列式

这一发现之所以被称为“天人般的洞察”，源于以下突破性特征：

 

• 从混沌到有序的提炼

在行列式理论尚未系统化的时代，Cramer通过观察具体方程组的解结构，从看似杂乱的系数组合中识别出统一的模式。例如对于二元方程组：

 

 

               

          

 

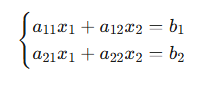
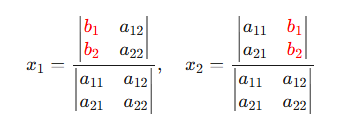
           等替换后的组合。这种模式在更高维度（n元）下依然成立，揭示了数学深层的对称性。
           

        

 

 

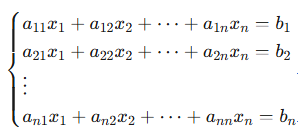
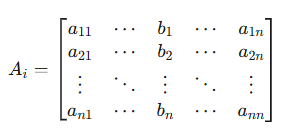
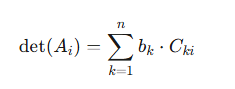
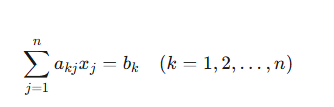
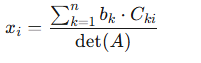
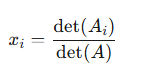
• 分类标准的建立

          Cramer法则隐含了一个分类判断标准：当分母（系数矩阵行列式）非零时，方程组有唯一解；为零时则对应无解或无穷解。这为线性方程组的解类型划分提供了明确的代数判据，将原本需要几何或代数技巧的判断转化为可计算的数值特征。

 

 

• 相对性思想的体现

          分子行列式通过替换列向量生成，体现了“相对调整”的数学思想。每个分量的解都对应着系数矩阵某一维度的局部修改，而整体解的构造则保持了与原始系统的相对协调性。这种设计暗合了概念相对性原则——解的表达始终以原系数矩阵为参考系。

 

二、发现过程中的关键思维突破

Cramer的突破可归结为三个层面的创新：

 

例如，在二元方程组中，解的表达式为：

​

Cramer注意到分母相同且具有对称的乘积结构，而分子则通过替换列实现局部调整。这种观察促使他猜想更高维度下的类似规律，并最终通过归纳法验证。

三、对数学发展的深远影响

1. 行列式理论的催化剂
   Cramer法则直接推动了行列式理论的系统化。数学家们为了解释其合理性，必须严格定义行列式的性质（如排列的奇偶性、逆序数符号等），最终形成了现代行列式理论。

2. 线性代数范式的转型
   该法则将解的存在性问题转化为行列式的计算问题，使代数研究从具体的方程求解转向抽象的矩阵分析。这种范式转型为后续向量空间、线性变换等概念的诞生奠定了基础。

3. 计算复杂度的启示
   虽然Cramer法则理论上完美，但其计算复杂度为O(n!)，暴露了行列式方法的局限性。这促使数学家寻求更高效的算法（如高斯消元法），推动了数值计算领域的发展。

四、结语

Cramer的发现之所以震撼，在于他跨越了经验观察与形式化定义之间的鸿沟。通过将具体问题的解结构与抽象的行列式符号相结合，他不仅解决了一类数学问题，更创造了一个新的数学分析框架。这种从混沌中提炼秩序、从特例中洞察普适规律的能力，正是数学史上“天人”级突破的典范。