皮尔逊χ²检验（Pearson's Chi-squared Test）
起源
皮尔逊χ²检验（Pearson's Chi-squared Test），也称为卡方检验，是由英国统计学家卡尔·皮尔逊（Karl Pearson）在19世纪末提出的。它是统计学中最常用的一种非参数检验方法，最初设计用于评估观察频数与期望频数之间是否存在显著差异，常用于推断分类变量间的独立性或拟合优度检验。
原理与定义
皮尔逊χ²检验的基本思想是通过比较观察频数与理论频数（即在原假设成立时预期的频数）之间的差异，来判断这种差异是否由随机抽样误差引起，还是反映了一个真实存在的效应。
公式
对于一个 (r times c) 列联表（行数为 (r)，列数为 (c)），χ²统计量的计算公式为：
其中，(O_{ij}) 是实际观测到的频数，(E_{ij}) 是在原假设下（通常指变量间独立）期望的频数，且 (chi^2) 遵循自由度为 ((r-1)(c-1)) 的χ²分布。
引申义
- **拟合优度检验**：检验样本数据是否符合某种理论分布。
- **独立性检验**：检验两个分类变量是否独立。
异同点
- 与t检验、Z检验相比，χ²检验适用于分类数据，不需数据满足正态分布。
- 与F检验类似，两者都是基于分布的检验，但F检验主要用于方差分析或多元回归的显著性测试，而χ²检验针对频率分布。
优缺点
**优点**:
- 简单直观，易于理解。
- 适用于分类数据，不受数据分布限制。
**缺点**:
- 对小样本或期望频数太小的情况敏感，可能导致检验结果不可靠。
- 只能处理分类数据，不适合连续数据。
应用场景
- 调查数据分析，如市场调研中顾客对不同产品的偏好是否与性别有关。
- 生物统计学，检验某种疾病与特定基因型之间是否存在关联。
- 社会科学，研究不同社会群体的态度、行为差异等。
数据演示
让我们通过一个具体例子来演示如何使用χ²检验（卡方检验）来分析数据。假设我们正在研究一个班级学生对两种不同学习方式（线上学习和线下学习）的偏好，以及他们期末考试成绩的等级（优秀、良好、及格、不及格）。我们的目的是检验学习方式与成绩等级之间是否存在关联。
收集数据
以下是收集到的样本数据（简化示例）：
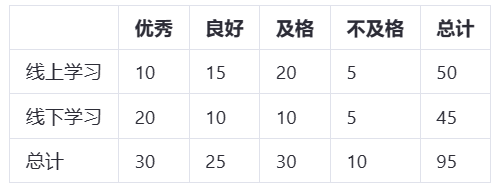
零假设 (H0)：学生的学习方式与其成绩等级之间没有关联。
备择假设 (H1)：学生的学习方式与其成绩等级之间存在关联。
计算步骤
-
计算期望频数：基于行和列的边际总和计算每一格的期望频数。
例如，线上学习且成绩优秀的期望频数计算为：
计算所有单元格的期望频数后，表格如下（具体数值需要计算后填写）。
-
计算χ²统计量：使用公式
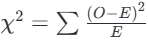其中 O 是观察频数，E 是期望频数。 -
确定自由度：自由度 = (行数 - 1) * (列数 - 1)。
-
查表或计算p值：根据χ²统计量和自由度，查阅χ²分布表或使用统计软件计算p值。
-
决策：如果p值小于显著性水平（如0.05），则拒绝零假设，认为学习方式与成绩等级之间存在显著关联。
实际计算
由于具体数值计算过程较繁琐，且需要精确计算工具，以下直接给出简化后的示例计算思路。实际中，你可以使用电子表格软件（如Excel）或者统计软件（如SPSS、R语言等）来进行这些计算。
计算期望频数示例
线上学习优秀期望频数计算示例已给出公式，实际计算需逐一完成。
χ²统计量示例
假设我们已经计算出所有期望频数并完成了χ²统计量的计算，得到的χ²值为某个具体数值（比如12.5）。
自由度
在这个例子中，有2行（线上学习、线下学习）和4列（优秀、良好、及格、不及格），因此自由度 = (2-1) * (4-1) = 3。
查表或计算p值
使用χ²分布表或统计软件，查得自由度为3时，χ²=12.5对应的p值。如果p值小于0.05，说明在0.05的显著性水平下，我们有足够的证据拒绝零假设，即认为学习方式与成绩等级之间存在显著的关联。
结论
基于上述步骤，如果你通过计算和查表或软件获得了p值，并发现它小于预设的显著性水平，那么可以得出结论，学生的学习方式（线上或线下）与他们的期末考试成绩等级之间存在统计学上的显著关联。
Java实现演示
在Java中实现χ²检验（卡方检验）通常涉及一些复杂的统计计算，可能不如直接使用专业的统计库来得高效和准确。但是，为了展示基本逻辑，我可以提供一个简化的示例代码，该代码将手动计算χ²统计量的部分逻辑。请注意，实际应用中推荐使用如Apache Commons Math或Jama等库来进行高级统计计算。
以下是一个简化的Java示例，仅展示了如何计算χ²统计量的基本框架，未包括所有细节，比如期望频数的精确计算、p值的查找等部分。
import java.util.Map;
public class ChiSquareTestExample {
// 假设我们有一个二维数组或映射来存储观察频数
private static final int[][] OBSERVED_FREQ = {
{10, 15, 20, 5}, // 线上学习
{20, 10, 10, 5} // 线下学习
};
public static void main(String[] args) {
calculateChiSquare();
}
private static void calculateChiSquare() {
int numRows = OBSERVED_FREQ.length;
int numCols = OBSERVED_FREQ[0].length;
int total = 0;
// 计算总频数
for (int[] row : OBSERVED_FREQ) {
for (int freq : row) {
total += freq;
}
}
// 初始化期望频数矩阵
int[][] expectedFreq = new int[numRows][numCols];
// 计算期望频数
for (int i = 0; i < numRows; i++) {
int rowTotal = 0;
for (int freq : OBSERVED_FREQ[i]) {
rowTotal += freq;
}
for (int j = 0; j < numCols; j++) {
expectedFreq[i][j] = (int)((double)rowTotal * OBSERVED_FREQ[j][i] / total);
}
}
// 计算χ²统计量
double chiSquare = 0;
for (int i = 0; i < numRows; i++) {
for (int j = 0; j < numCols; j++) {
chiSquare += Math.pow(OBSERVED_FREQ[i][j] - expectedFreq[i][j], 2) / expectedFreq[i][j];
}
}
System.out.println("χ²统计量: " + chiSquare);
// 注意：此处未包含自由度计算和p值查找，实际应用中应使用专业统计库完成
}
}
这段代码展示了如何手动计算χ²统计量的过程，包括计算观察频数的总和、期望频数，以及最终的χ²统计量。然而，对于p值的计算和临界值的判断，通常需要使用更高级的统计方法或现成的统计库，因为这涉及到复杂的分布函数计算和临界值查找。此外，这个示例简化了许多实际应用中的复杂情况，如处理小样本或期望频数过小的问题。
常见的相似度计算方法
余弦相似度（Cosine Similarity）
皮尔逊相关系数
曼哈顿距离（Manhattan Distance）
欧氏距离（Euclidean Distance）
修正余弦相似度（Adjusted Cosine Similarity）
皮尔逊χ²检验（Pearson's Chi-squared Test）
