ReLU 和 dropout 层在 CNN 中的工作原理-AI快速进阶系列

1. 概述

在本教程中，我们将使用示例网络架构研究卷积神经网络的两个基本组件——ReLU（Rectified Linear Unit） 与 Dropout 层。

到最后，我们将了解它们插入CNN背后的基本原理。此外，我们还将知道在我们自己的卷积神经网络中实现它们需要哪些步骤。

2. CNN中的维度诅咒

在构建任何神经网络时，我们必须假设两个基本假设：

1 – 输入特征的线性无关

2 – 输入空间的低维

我们通常使用 CNN 处理的数据（音频、图像、文本和视频）通常不满足这些假设中的任何一个，这正是我们使用 CNN 而不是其他 NN 架构的原因。

在CNN中，通过在训练期间执行卷积和池化，隐藏层的神经元通过其输入学习可能的抽象表示，这通常会降低其维数。

然后，网络假设这些抽象表示，而不是底层输入特征，彼此独立。这些抽象表示通常包含在CNN的隐藏层中，并且往往具有比输入更低的维度：

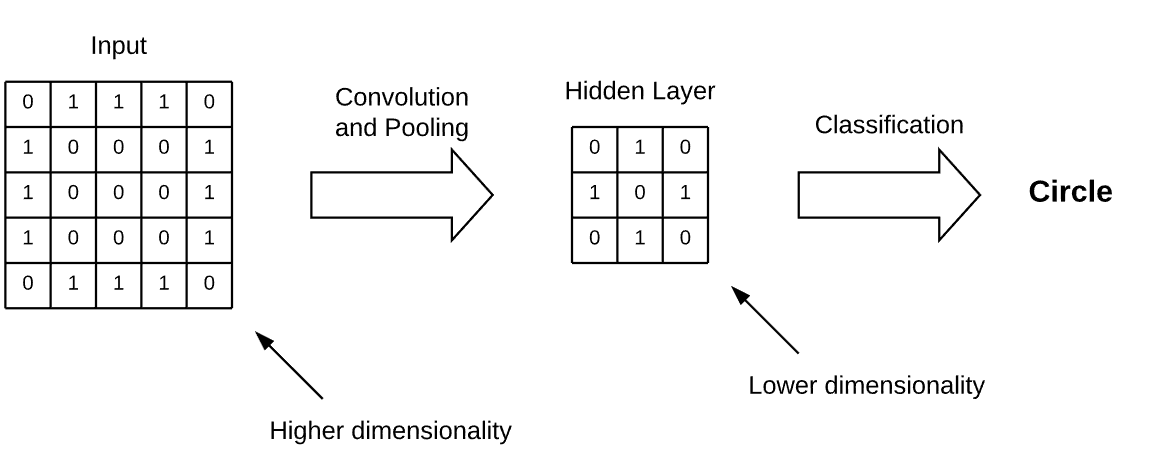
因此，CNN有助于解决所谓的“维度诅咒”问题，该问题是指执行机器学习任务所需的计算量与输入维度的单位增加相关的指数增长。

3. ReLU

3.1. 为什么不在cnn中使用Sigmoidal函数?

经过训练的CNN具有隐藏层，其神经元对应于输入特征上可能的抽象表示。当面对一个看不见的输入时，CNN不知道它所学到的抽象表示中哪一个与特定的输入相关。对于隐藏层中的任何给定神经元，表示给定的学习抽象表示，有两种可能的(模糊)情况:要么神经元是相关的，要么它不是。如果神经元不相关，这并不一定意味着其他可能的抽象表征也不太可能。如果我们使用一个激活函数，其图像包含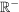，这意味着，对于神经元的某些输入值，该神经元的输出将对神经网络的输出产生负贡献。

这通常是不可取的:如上所述，我们假设所有学习到的抽象表示都是彼此独立的。对于cnn，因此最好使用非负激活函数。

此类函数中最常见的是整流线性函数，使用它的神经元称为整流线性单元(ReLU)， f(x) = argmax(0,x):

 

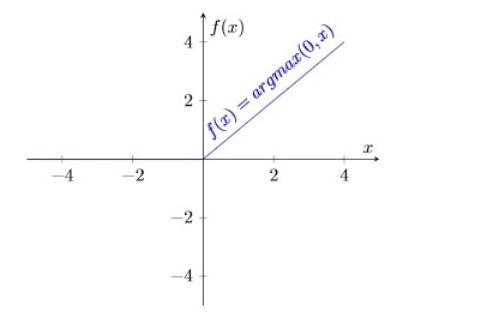
3.2. 计算 ReLU

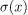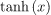与或等sigmoidal 函数相比，该函数有两个主要优点。

1. ReLU的计算非常简单，因为它只涉及输入和值0之间的比较。

2. 它的导数为0或1，这取决于它的输入是否分别为负。

后者，特别是对训练中的反向传播有重要的影响。这实际上意味着计算神经元的梯度在计算上是廉价的:

 

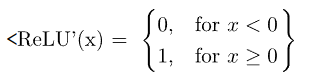
非线性激活函数，如sigmoidal 函数，相反通常没有这个特征。

因此，使用ReLU有助于防止操作神经网络所需的计算的指数增长。如果CNN按规模扩展，添加额外relu的计算成本会线性增加。

ReLU还可以防止所谓的“梯度消失”问题的出现，这在使用sigmoid函数时很常见。这个问题是指对于高输入值，神经元的梯度趋向于接近零。

虽然 sigmoid函数的导数在接近正无穷大时趋于 0，但 ReLU 始终保持在恒定的 1。这允许错误的反向传播和学习继续，即使对于激活函数的输入值很高：

 

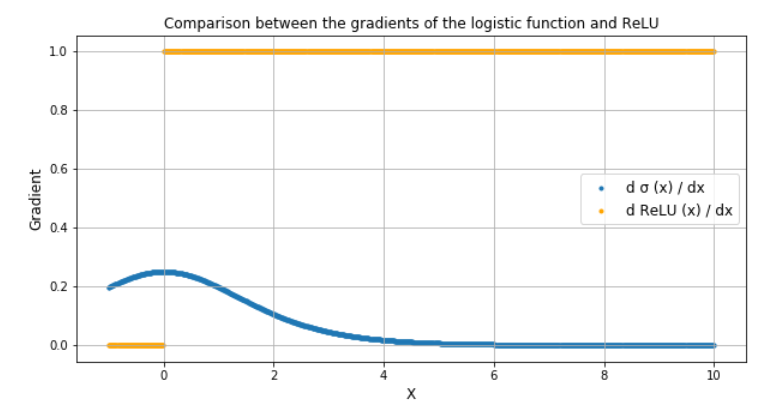
4. Dropout 层

CNN的另一个典型特征是Dropout层。Dropout 层是一个掩码，它使某些神经元对下一层的贡献无效，并使所有其他神经元保持不变。我们可以将 Dropout 层应用于输入向量，在这种情况下，它会使其某些特征无效;但是我们也可以将其应用于隐藏层，在这种情况下，它会使一些隐藏的神经元无效。

辍学层在训练 CNN 中很重要，因为它们可以防止训练数据过度拟合。如果它们不存在，第一批训练样本会以不成比例的方式影响学习。反过来，这将阻止学习仅在以后的样本或批次中出现的特征：

 

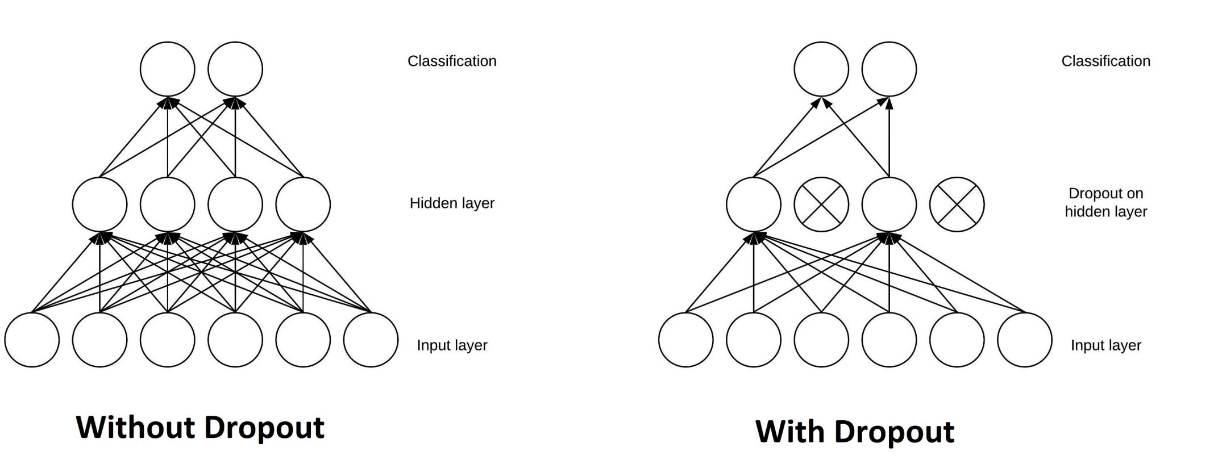
假设我们在训练期间连续向 CNN 展示十张圆圈图片。CNN不会知道直线的存在;因此，如果我们稍后向它展示一张正方形的图片，那将非常混乱。我们可以通过在网络架构中添加 Dropout 层来防止这些情况，以防止过度拟合。

5. 具有ReLU和Dropout层的CNN

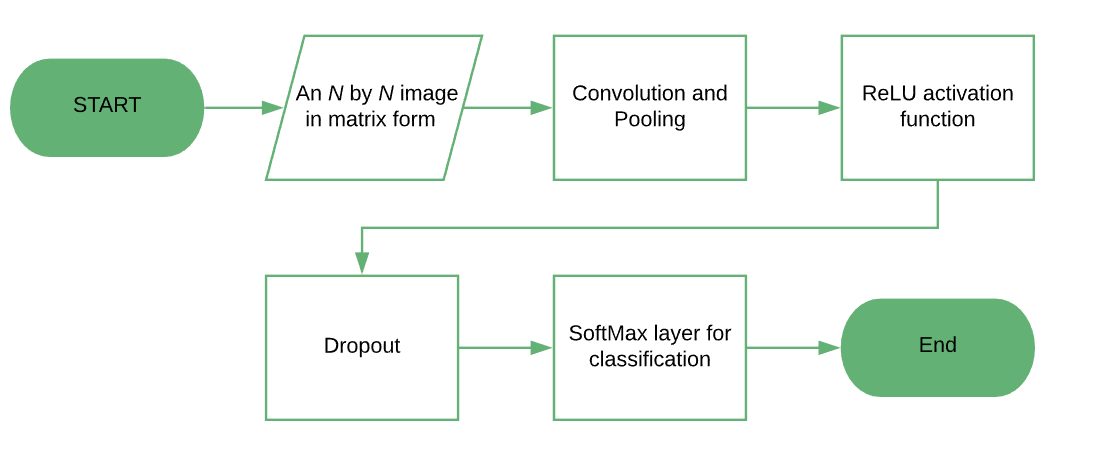
此流程图显示了具有 ReLU 和 Dropout 层的 CNN 的典型架构。这种类型的架构在图像分类任务中非常常见：

 

 

6. 结论

在本文中，我们已经看到了我们什么时候更喜欢 CNN 而不是 NN。当输入的功能不独立时，我们更喜欢使用它们。我们还了解了为什么我们使用 ReLU 作为激活函数。

ReLU易于计算，并且具有可预测的误差反向传播梯度。

最后，我们讨论了 Dropout 层如何防止在训练期间过度拟合模型。值得注意的是，Dropout 随机停用了一层的某些神经元，从而抵消了它们对输出的贡献。