最小最大值算法-AI快速进阶系列
1. 概述
在人工智能和博弈论领域，我们经常遇到搜索问题。这些问题可以用互连节点的图来描述，每个节点代表一种可能的状态。
智能代理需要能够通过评估每个节点来遍历图，以达到“良好”（如果不是最佳）状态。
但是，存在无法应用典型图形搜索算法的特定类型的问题。
在本教程中，我们将讨论此类问题并评估可能的解决方案之一 – Minimax 算法。
2. 简介
在本教程中，我们将讨论最小最大值算法，这是一种处理对抗性问题的相当简单的方法。“对抗性”是指多智能体系统，其中每个智能体通过考虑对手的可能行动来选择他们的策略。
效用函数指示一个状态对代理来说有多“好”。在二人博弈中，代理人试图最大化效用函数，而他的对手试图最小化效用函数。这个算法名字背后的原因显而易见。
在本教程中，我们将讨论极大极小算法，这是处理对抗问题的一种相当简单的方法。“对抗性”指的是多智能体系统，其中每个智能体通过考虑对手可能的行动来选择自己的策略。
3. 示例
让我们考虑一个例子来了解算法是如何工作的。两个玩家Max和Min正在玩一个可以用树表示的游戏，如下图所示：
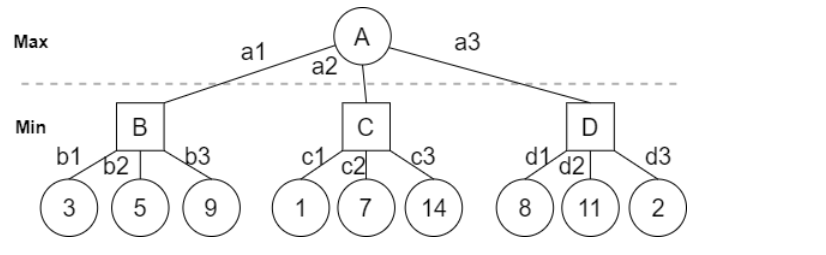
圆圈表示这是Max的移动，正方形表示Min的移动。当到达终端（叶）节点时，游戏结束。终端值是写在叶节点下方的实用程序函数的值。
在 Max 和 Min 都发挥最佳状态的设置中，无论 Max 采取什么动作，Min 都会选择产生最低效用分数的反移动。因此，我们可以通过遵循自上而下的方法来决定最佳举措。
我们首先遍历树的深度，直到到达终端节点，并为它们的父节点分配一个最适合轮到玩家移动的值。
在这种情况下，如果 Max 选择B，那么 Min 会选择b1，因为这是可能的最低值。因此，我们分配B=3。如果Max选择C，那么Min会选择c1等等：
计算完Min的走法后，我们可以继续为Max选择最佳走法，其表达式如下:
计算完Min的走法后，我们可以继续选择最优的走法。因此，Max将选择B, Min将选择b1，这个游戏的终端值将是3。
4. 实施细节
了解了算法的基本功能后，让我们用更正式的术语来表达它。就其性质而言，Minimax是一种深度优先搜索，可以方便地编码为递归函数。以下伪代码总结了该过程：
状态树的所有节点必须至少被访问一次。对于深度为d，每个节点有n个子节点的树，这相当于O(d^n)的计算复杂度。
5. 改进
很容易看出，必须访问每个节点的算法不是很有效。在实际应用中出现的树非常深，也非常宽。一个很好的例子就是嘀嗒字游戏。这当然是一个简单的游戏，但与之相关的状态图非常复杂，有9!必须访问的节点。
虽然这个问题不能完全解决，但可以通过丢弃冗余且不能提供更好解决方案的节点子树来缓解。这个过程被称为Alpha-Beta剪枝。
让我们再回顾一下前面的例子:
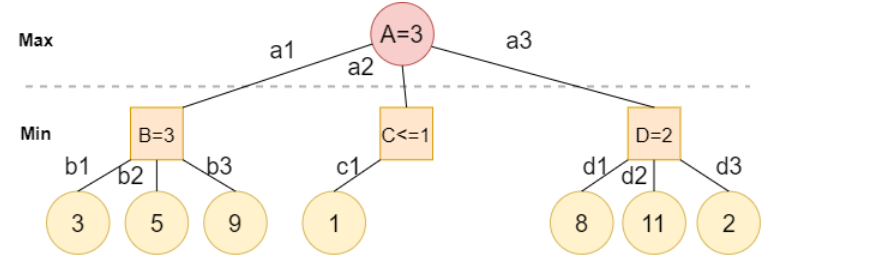
当尝试计算节点C时，我们注意到第一个子节点是c1=1。Min想要最小化效用分数，所以他肯定会选择c1，除非出现更低的值，所以我们可以说节点C的最终值将是
。
然而，节点B = 3对于Max来说是一个更好的选择，因为它的值大于C。因此，我们可以完全跳过C的其余子结点，因为它们不会提供任何更好的移动。前往节点D，它的每个子节点都将被评估，因为我们不能排除出现更好解决方案的可能性。
我们成功地跳过了2个节点的计算，从而降低了问题的计算量。这看起来可能不是什么大成就，但在更复杂的应用程序中，好处可能相当显著。
6. 限制
尽管 alpha-beta 修剪减轻了计算成本，但它只允许算法在合理的时间限制内更深入地检查几层。指数级的计算复杂性限制了算法对层数很少的游戏的能力。
具有令人难以置信的深度状态树或涉及偶然性的游戏往往超出了算法的能力。在此类问题中，我们需要启发式地评估节点，就好像它们是终端节点一样。这允许算法在有限深度下检查状态，并选择良好但不是最佳解决方案。
7. 结论
在本文中，我们讨论了 Minimax 算法的功能以及通常应用它的领域。然后，我们回顾了它的弱点，并介绍了一种通常用于解决这些问题的修剪技术。最后，我们讨论了算法的局限性以及为更高级和计算上可行的算法奠定基础的解决方案。
