POJ1177 Picture

题目链接

题目

Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

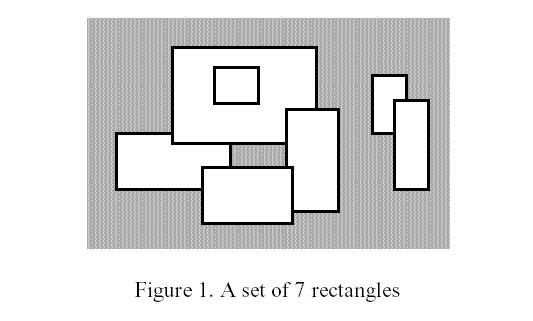
The corresponding boundary is the whole set of line segments drawn in Figure 2.

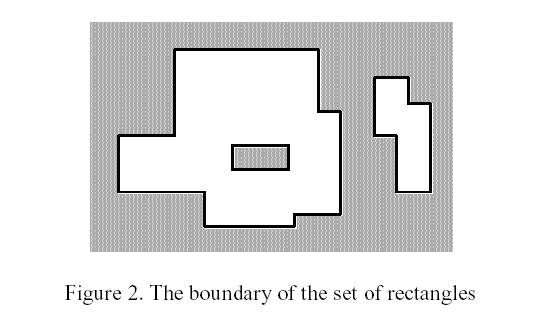
The vertices of all rectangles have integer coordinates.

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.

0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

Sample Input

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

Sample Output

228

Source

IOI 1998

题解

知识点：线段树，扫面线，离散化。

线段树+扫描线求周长并，是板子题。

更新时，通过区间连续覆盖段数、线段覆盖长度、上次更新的距离，计算周长并。

时间复杂度 \(O(n\log n)\)

空间复杂度 \(O(n)\)

代码

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

template<class T>
struct Discretization {
    vector<T> uniq;
    Discretization() {}
    Discretization(const vector<T> &src) { init(src); }
    void init(const vector<T> &src) {
        uniq = src;
        sort(uniq.begin() + 1, uniq.end());
        uniq.erase(unique(uniq.begin() + 1, uniq.end()), uniq.end());
    }
    int get(T x) { return lower_bound(uniq.begin() + 1, uniq.end(), x) - uniq.begin(); }
};

template<class T>
class ScanlineC {
    struct Segment {
        int l, r;
        int cover;
        bool lc, rc;
        int cnt;
        T len;
    };

    int n;
    vector<T> dot;
    vector<Segment> node;

    void push_up(int rt) {
        if (node[rt].cover) {
            node[rt].lc = node[rt].rc = 1;
            node[rt].cnt = 1;
            node[rt].len = dot[node[rt].r + 1] - dot[node[rt].l];
        }
        else if (node[rt].l == node[rt].r) {
            node[rt].lc = node[rt].rc = 0;
            node[rt].cnt = 0;
            node[rt].len = 0;
        }
        else {
            node[rt].lc = node[rt << 1].lc, node[rt].rc = node[rt << 1 | 1].rc;
            node[rt].cnt = node[rt << 1].cnt + node[rt << 1 | 1].cnt - (node[rt << 1].rc && node[rt << 1 | 1].lc);
            node[rt].len = node[rt << 1].len + node[rt << 1 | 1].len;
        }
    }

    void update(int rt, int l, int r, int x, int y, int cover) {
        if (r < x || y < l) return;
        if (x <= l && r <= y) return node[rt].cover += cover, push_up(rt);
        int mid = l + r >> 1;
        update(rt << 1, l, mid, x, y, cover);
        update(rt << 1 | 1, mid + 1, r, x, y, cover);
        push_up(rt);
    }

public:
    ScanlineC() {}
    ScanlineC(const vector<T> &_dot) { init(_dot); }
    void init(const vector<T> &_dot) {
        assert(_dot.size() >= 3);
        n = _dot.size() - 2;
        dot = _dot;
        node.assign(n << 2, { 0,0,0,0,0,0,0 });
        function<void(int, int, int)> build = [&](int rt, int l, int r) {
            node[rt] = { l,r,0,0,0,0,0 };
            if (l == r) return;
            int mid = l + r >> 1;
            build(rt << 1, l, mid);
            build(rt << 1 | 1, mid + 1, r);
        };
        build(1, 1, n);
    }

    void update(int x, int y, int cover) { update(1, 1, n, x, y, cover); }

    Segment query() { return node[1]; }
};
/// 周长并扫描线特化线段树，修改查询O(logn)，配合离散化可以处理任意精度覆盖长度并、覆盖线段条数问题
/// 求周长并，O(nlogn)，周长并 = sum(两次扫描覆盖长度并的差的绝对值+两次扫描的距离*覆盖线段条数)
//* 其中n代表线段数，并非端点数，端点数应为n+1
//* 端点编号从1开始，线段编号也从1开始
//* 任何区间（如l,r或x,y）都代表线段编号而非端点编号，即表示dot[l]到dot[r + 1]，使用时注意
//* 修改dot[l]到dot[r]时，应是update(l,r-1,?)

template<class T>
struct pk {
    T val;
    friend bool operator<(const pk &a, const pk &b) {
        if (abs(a.val - b.val) < 1e-6) return false;//! 浮点型注意相等条件
        return a.val < b.val;
    }
    friend bool operator==(const pk &a, const pk &b) { return !(a < b) && !(b < a); }
};
//* 专门处理浮点型比较判断的封装类

template<class T>
struct edge {
    T x;
    pk<T> y1, y2;
    int flag;
};

int main() {
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    vector<edge<int>> e(2 * n + 1);
    vector<pk<int>> y_src(2 * n + 1);
    for (int i = 1;i <= n;i++) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        e[2 * i - 1] = { x1,{y1},{y2},1 };
        e[2 * i] = { x2,{y1},{y2},-1 };
        y_src[2 * i - 1] = { y1 };
        y_src[2 * i] = { y2 };
    }

    Discretization<pk<int>> dc(y_src);
    sort(e.begin() + 1, e.end(), [&](const auto &a, const auto &b) {return a.x < b.x;});

    vector<int> dot(dc.uniq.size());
    for (int i = 1;i < dot.size();i++) dot[i] = dc.uniq[i].val;
    ScanlineC<int> slc(dot);
    slc.update(dc.get(e[1].y1), dc.get(e[1].y2) - 1, e[1].flag);
    ll ans = slc.query().len;
    for (int i = 2;i <= 2 * n;i++) {
        ans += 2LL * (e[i].x - e[i - 1].x) * slc.query().cnt;
        ll len = slc.query().len;
        slc.update(dc.get(e[i].y1), dc.get(e[i].y2) - 1, e[i].flag);
        ans += abs(slc.query().len - len);
    }
    cout << ans << '\n';
    return 0;
}

/*
7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

228
 */