POJ1456 Supermarket

题目链接

题目

Description

A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σx∈Sellpx. An optimal selling schedule is a schedule with a maximum profit.

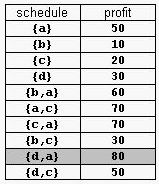
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80.

Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products.

Input

A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.

Output

For each set of products, the program prints on the standard output the profit of an optimal selling schedule for the set. Each result is printed from the beginning of a separate line.

Sample Input

4  50 2  10 1   20 2   30 1

7  20 1   2 1   10 3  100 2   8 2
   5 20  50 10

Sample Output

80
185

Hint

The sample input contains two product sets. The first set encodes the products from table 1. The second set is for 7 products. The profit of an optimal schedule for these products is 185.

Source

Southeastern Europe 2003

题解

方法一

知识点：并查集，贪心。

这道题和并查集结合起来还是挺妙的。

首先考虑一个贪心，每次先安排价值最高的。如此选择，如果一个货物在期限之前无法安排，那说明其期限之前的所有天数都被比他价值高的货物占据了，此时这个货物可以被抛弃，强行售出只会降低总收益。

为了判断货物是否存在某天能够被安排，需要知道其距离期限最近的一个可用天数，因为如果选过早的话，可能会把其他期限靠前的货物的机会使用掉。考虑使用并查集维护从过期时间向前数的第一个未占用位置，如果第一个未被占用位置为 \(0\) 则说明没有位置。

时间复杂度 \(O(n \log n)\)

空间复杂度 \(O(n)\)

方法二

知识点：贪心，优先队列。

典型的后悔贪心题。花费是常数 \(1\) ，限制和收益是变量。使用小顶堆维护后悔操作，按从限制从小到大排序入队。

时间复杂度 \(O(n\log n)\)

空间复杂度 \(O(n)\)

代码

方法一

#include <bits/stdc++.h>

using namespace std;

struct node {
    int p, d;
}a[10007];

int fa[10007];

bool cmp(node a, node b) {
    return a.p > b.p;
}

int find(int x) {
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

void merge(int x, int y) {
    fa[find(x)] = find(y);
}

int main() {
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    while (cin >> n) {
        for (int i = 1;i <= 1e4;i++) fa[i] = i;///注意是天数的集合
        for (int i = 1;i <= n;i++)  cin >> a[i].p >> a[i].d;
        sort(a + 1, a + n + 1, cmp);
        int sum = 0;
        for (int i = 1;i <= n;i++) {
            int r = find(a[i].d);
            if (r) {
                merge(r, r - 1);///以之前的第一个可用天为根，即把之前的第一个可用天当作从此天开始的可用天
                sum += a[i].p;
            }
        }
        cout << sum << '\n';
    }
    return 0;
}

方法二

#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

struct node {
    int p, d;
}a[10007];

bool cmp(node a, node b) { return a.d < b.d; }

int main() {
    std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    while (cin >> n) {
        for (int i = 0;i < n;i++) cin >> a[i].p >> a[i].d;
        sort(a, a + n, cmp);
        priority_queue<int, vector<int>, greater<int> > pq;
        int sum = 0, ans = 0;
        for (int i = 0;i < n;i++) {
            pq.push(a[i].p);
            sum += a[i].p;
            while (pq.size() > a[i].d) {
                sum -= pq.top();
                pq.pop();
            }
            ans = max(ans, sum);
        }
        cout << ans << '\n';
    }
    return 0;
}