Border & 最小后缀
Border & 最小后缀
https://www.luogu.com.cn/blog/command-block/border-li-lun-xiao-ji
Border
- S[1,p] 是 border <=> S 有周期 len-p。
- S 的长度大于等于 n/2 的 border 长度构成一个等差数列。
- S 的所有 border 排序后组成的数组，可以划分成 \(O(\log{len})\) 个等差数列。
- S 公差大于等于 d 的 border 等差数列的总长度是 \(O(\frac{n}d)\) 的。
- 回文 border 理论：S 的回文后缀长度集合，可以划分成 \(O(\log len)\) 个等差数列。
最小后缀
设 \(ssuf(S)\) 为【存在一种 在 S 后面加一个串 的方案，使得此后缀为最小后缀】的后缀集合。
则 \(|ssuf(S)|\le O(\log len)\)
例题： ZJOI2017 字符串；节日庆典。
CF917E - Upside Down
https://www.luogu.com.cn/problem/CF917E
这道题不评 3500？？？还是我目光短浅了！！！
三种情况，一种是 \(u\) 是 \(v\) 的祖先，一种是 \(v\) 是 \(u\) 的祖先，还有以上都不是。（upd：其实不是这样的，是对于一个询问，拆成上面三种情况之和）
对于前面两种：
硬点 \(u\) 是 \(v\) 的祖先，如果不是就把 \(s_k\) 反过来。那么答案就是 \(ans(1,v)-ans(1,u+|s_k|-2)\)，后面那个指的是 \(u-v\) 的路径上，\(u\) 的第 \(u+|s_k|-2\) 个儿子，也就是 \(v\) 的第 \(dep_v-dep_u-|s_k|+1\) 个祖先。
于是我们要处理根到 \(x\) 的答案，那么我们 dfs 向前走，对应在 AC 自动机上向前走（回溯的时候就是返回），并给走过的点加权。并把树上的点的询问处理一下。
具体：走的时候给点加一，询问的时候查询对应点的 \(fail\) 树和，用树状数组即可维护。
对于后面一种：
对于一组询问 \((u,v,lca,s)\)。我们预处理出 \(u \to lca\) 的后缀 与 s 的前缀 的 极长匹配串 \(A\)；预处理出 \(lca\to v\) 的前缀 与 s 的后缀 的 极长匹配串 \(B\)。（预处理方法见后文）
我们知道将串 T 的长度为 x 的前缀和长度为 y 的后缀拼起来，如果 \(x+y=|T|\)，那么拼起来的串就等于 T。
所以我们求出 A 的 border：\(A'\)，以及 B 的 border：\(B'\)，那么 \(A',B'\) 肯定是 s 的前缀和后缀，而且他们可以通过 lca 处拼接起来。所以我们找到所有的 \(|A'|+|B'|=|s|\) 的 border 就可以了。
由于 border 可以变成 log 段等差数列，那么我们暴力地枚举 A 和 B 的每一段等差数列，那么就相当于求 \(x_1+y_1p+x_2+y_2q=|s|\) 的解（upd：\(p,q\) 是变量），用 exgcd 求出一组解然后算出方案数即可。\(O(\log^2)\)
至于 \(p,q\) 怎么求？相当于是，我要求某个串的前缀的所有 border（后缀就是反串的前缀），那我直接暴力地搞就好了。我的 border 集合就是我的最长 border 并上我的最长 border 的最长 border 集合。然后暴力继承状态就好了，因为是 \(O(\log)\) 的所以可以（吧？）。
怎么预处理出 A，B？（下文说 B，A 可以举一反三）
我们建出 \(s\) 的后缀数组，然后就可以二分出 B 可以匹配到 \(s\) 的哪个位置。check 的方式就是找到 【当前二分到的后缀 \(B'\)】与 \(lca\to v\) 的大小关系，也就是比对 lcp 的下一位。用 hash + 二分即可。\(O(\log^2)\) 。
但是找到匹配的位置后，可能 \(B'\) 的长度大于 \(lca\to v\)，于是就跳到 \(B'\) 的最大 border。如果还是大于，那就再跳到最大 border...一直跳到 \(B'\) 的长度小于等于 \(lca\to v\) 为止。因为求 border 可以用 KmP 实现，所以倍增 KmP 即可。倍增 KmP 就相当于连边 \(i\to kmp_i\) 后 \(i\) 的 \(2^j father\)。
代码：http://www.gdfzoj.com/submission/131585 当然是没有调试的，因为实在是太 NT 了!
loj6681 - yyw 与回文串
考虑点分治，跨过分治中心的点 \(c\) 的回文串有多少。
那么回文串肯定是这样的：比如某个子树的 \(u\) 到另一个子树的 \(v\) 是回文串，且 \(|s[u\to c]|>|s[c\to v]|\) 那么 \(s[u\to c]=T+S,s[c\to v]=S\) 其中 \(T\) 是一个回文串。
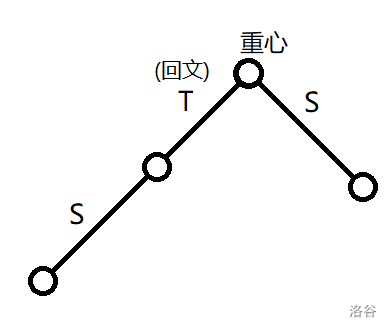
我们把前面的子树都塞进 ACAM 中（对应的结束节点权值加一），于是考虑当前 dfs 的子树的贡献。
边走边在 ACAM 上对应地走。
如何判断现在的串是不是一个回文串？用哈希判断正串与反串是否全等即可！
我们维护现在所有的回文后缀，那么如果我现在 dfs 到的字符串长度为 \(l\)，而某一个回文后缀长度为 \(x\)，那么贡献就是 ACAM 点的 \(l-x\) 辈祖先的权值。
但是可能有千军万马的回文后缀。不过，根据 Border 定理 5，可以变成 Log 个等差数列。
于是我们记录所有等差数列的 首项 \(a_0\)，公差 \(d\)，末项 \(a_a\)，然后我就看 ACAM 点的 \(l-a_0,l-a_0-d,l-a_0-d-d...\) 辈祖先即可。也就是 \(x\) 辈祖先，\(x\bmod d=a_0\bmod d,x\in [l-a_0,l-a_a]\)。
对于 \(d\le sqrt(n)\) （实测 \(d\le 4\) 更快）的，我们开一个桶，就是 \(box[i][j]\) 就是 \(\% i=j\) 的祖先的权值和。
对于 \(d\le sqrt(n)\) 的暴力即可。
CF1286E - Fedya the Potter Strikes Back
https://www.luogu.com.cn/problem/CF1286E
对于第 \(n\) 次操作，答案就是 \(n-1\) 的答案加上 \(s[1,n]\) 的 border。
定义一个 border 的颜色，就是其下一个字符是什么。
于是每次都将 \(n\) 插入 KmP 自动机，找到所在点 到根 的所有颜色不等于 \(s[n]\) 的点，将其对应的 border 删除（不是在自动机上删除）。
现在有两个问题：
- KMP 树上的节点为什么不需要删除？
- 删除后，剩下 border 集合，是否需要全部 +1？
- 代码中为什么写
del(i-u)？
答案：
- 如果一个 border 被删除了，他可能之后又会被加上来，所以不用删除。但是如何证明其正确性？显然我每一次都会把 \(i\) 号节点接在他的 border 上面，所以是正确的（原来这么简单，亏我想了好久）。
- 不需要，我们每一次会把 \(i\) 号节点接在他的 border 上面，所以对应的 border 集合，其实就是他的祖先们。
- 因为 border 的长度是
i-u。
CF1043G - Speckled Band
https://www.luogu.com.cn/problem/CF1043G
如果 \([l,r]\) 中没有相同的字母，那么就无解，显然。下面讨论有解情况！
答案肯定不超过四，因为我可以找到任意两个相同的字母的位置 \(x,y\)，最劣答案就是 \([l,x-1],[x,x],[x+1,y-1],[y,y],[y+1,r]\)，其中 \([x,x],[y,y]\) 是本质相同的，所以答案是 4.
然后我们依次 check 能不能有更优解：
-
ans=1即 AAAA，枚举 len 的所有质因子，看是否有这个周期。这是 \(O(\sqrt n)\)。 -
ans=2即 AAB，BAA，ABA。对于前两者：预处理出 \(L_i,R_i\) 代表从 \(i\) 开始 向左/向右 最短的 AA 串长度。
对于后者：要求出最 \([l,r]\) 的 border。
-
ans=3即 ABAC，BACA，BAAC。对于前两者：A肯定是单个字母。于是判断是否有一个和开头相同的字母；是否有一个和末尾相同的字母即可！
对于后者：找到中间一个位置 \(i\) 使得 \(R_i\le r\)，ST 表即可。
-
ans=4如果上面的所有的一切的最终的全部的情况全部判定失败那么就是 4。
于是我们发现最难处理的就是 ans=2 的情况。会了 ans=2 其它都迎刃而解，大闹天宫！
求 \(L_i,R_i\)：
我们枚举 A 的长度为 len，然后每隔 len 就设立一个关键点：
-----O-----O-----O----...
如果一个串包含两个关键点，那么他就有可能是一个 AA 串。
对于两个关键点间组成的串，我们算出他的 LcS 和 LcP：二分+Hash。据说可以用 Height 数组 ST 地 \(O(1)\) 处理，但是因为我连 Height 都不知道是什么，只好遗憾地向世界谢幕。
如果 LcS+LcP \(\ge\) len 那么就是一个可行的方案。具体看https://www.luogu.com.cn/problem/solution/P1117。
出现的区间是：从 lcs 开始 +2Xlen，直到现在位置 +2Xlen 大于 lcp 为止。
也就是：\(i-lcs\sim i+lcp-len+1\) 。
注：这里我还是没理解……
求 \([l,r]\) 的最短 Border：
有一个奇怪的做法：先判断有没有 \(1\sim sqrt(len)\) 的 border，如果没有，那么最短 border 与原串的后缀排名小于 \(sqrt(len)\)。
问题：这里的后缀排名是 \(s[l,r]\) 的后缀排名，还是 \(s[1,n]\) 的后缀排名？
经过瞪眼代码，是 \(s[1,n]\) 的。
比如 abbabbabbabb，然后 \(sqrt(len)=2\)（就先这样假设着），那么最短 border 是 abb，其它 border 还有 abbabb，abbabbabb 等等……
待填。。。
P4156 - 论战捆竹竿
https://www.luogu.com.cn/problem/P4156
显然我们求出所有的周期（即 n-|border|），然后就变成了同余最短路。
设周期集合为 \(a_i\)，我们即求 \(\sum a_ix_i\le w\) 的方案数（其中 \(w:=w-n\)）。
暴力去连边可以得到 30分的好成绩。
因为这样是 \(O(n^2)\) 的。
但是由于周期可以变成 \(O(\log )\) 个等差数列。我们对于每一个等差数列分别考虑！
假设现在有一个等差数列 \(a_0,a_0+d,a_0+2d,a_0+3d...a_0+kd\)，那么在 \(\bmod a_0\) 的剩余系下，我们可以得到 \(\gcd(d,w)\) 个环。对于每个环我们用 \(O(环长)\) 的时间复杂度去考虑，那么总共就是 \(O(n\log n)\) 的！
那么怎么样考虑呢？我们相当于用 \(dis_i\) 去更新 \(dis_{i+x}\) 什么的，显然 \(dis\) 最小的点是不会被更新的。
而且，在一个环中，相当于我们每次可以走 \(d,2d,3d...kd\) 步。那么用一个单调队列维护即可。
那么怎么从一个 \(a\) 剩余系转移到 \(b\) 剩余系？
考虑 \(dis_i\) 的意义，就是达到 \(\pmod a\) 的意义下，余 \(i\) 的最小数字是什么。那么 \(dis_x\to dis_{dis_x\bmod b}\) 即可。
PS：这道题好像只是用字符串做表象，掩盖其是毒瘤图论题的真相 23333
