后缀树 学习笔记

广告

是否遇见字符串就头疼？

是否在阅读 SAM 时被 endpos 和 parent-tree 搞得心肌梗塞？

而后缀树可以解决您的困扰！

它更像是压缩了的 AC自动机，但是可以和 SAM 一样用。它的 LCA 是后缀的最长公共前缀，遍历它的 dfs序 是 SA！

而且，它比 SAM 更容易理解，更直观简单，更便于扩展，更适合新手。

那么，就来学习后缀树吧！

EA 讲解后缀树（其实这里已经超级清晰了），这里借用了一些 EA 的图片，在此致谢。

印象

我们把 banana 的所有后缀插入到了一个 Trie 中，显得十分优美。

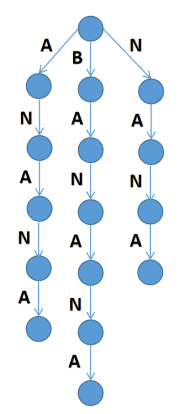
但是，有很多后缀没有显示出来，比如 na 就被 ana 覆盖了。于是我们把原串变成 banana$ 就可以了。

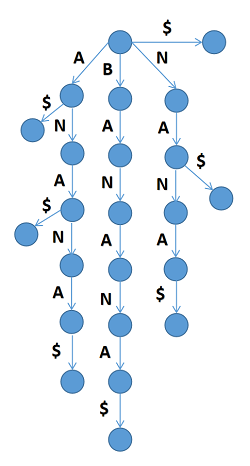
但是显然这样很浪费（节点数为 \(O(n^2)\)）。我们可以把链给压缩起来（就像虚树那样）：

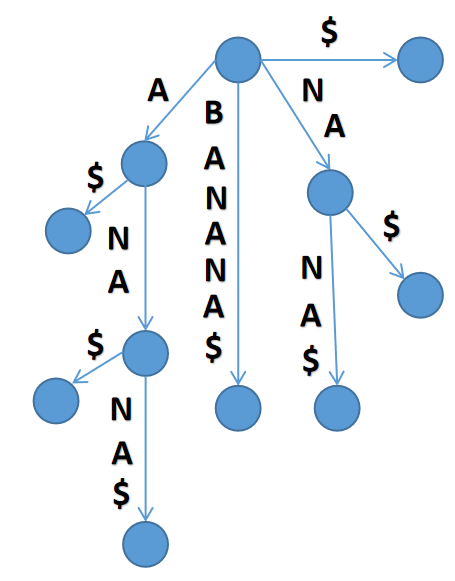
顿时，节点的数量很少了。它最多有 \((2n+1)\) 个节点。可以这样证明：每次插入后缀就相当于插入一个链，则 \(n\) 个链的虚树就是 \((2n+1)\) 个节点。

这，就是直观而浅显，却仍蕴含着万千奥秘的后缀树。

Q&A

• 如果遇到 abbb 这种，最后会不会 return; 导致没有插入完？

  不会，因为事实上是 abbb$。

代码

快进到代码实现 （神奇）

struct SFXTRE{
	struct beer{int fail,beg,len,son[27];}dot[n7*2];
	int cnt,rem,las,now;
	
	SFXTRE(){dot[0].len=inf,cnt=1,now=1;}

	int Dnew(int begz,int lenz){
		cnt++,dot[cnt]=(beer){1,begz,lenz};
		return cnt;
	}

	void isert(int id){
		rem++,las=1;
		while(rem){
			while(rem>dot[ dot[now].son[ cr[id-rem+1] ] ].len){
				now=dot[now].son[ cr[id-rem+1] ];
				rem-=dot[now].len;
			}
			int &z=dot[now].son[ cr[id-rem+1] ];
			char ch=cr[ dot[z].beg+rem-1 ];
			if(!z||cr[id]==ch){
				dot[las].fail=now,las=now;
				if(!z)z=Dnew(id,inf);
				else return;
			}			 
			else{
				int fut=Dnew(dot[z].beg,rem-1);
				dot[fut].son[ch]=z;
				dot[fut].son[ cr[id] ]=Dnew(id,inf);
				dot[z].beg+=rem-1,dot[z].len-=rem-1;
				z=fut,dot[las].fail=fut,las=fut;
			}
			if(now==1)rem--;
			else now=dot[now].fail;
		}
	}
}tre;

---

struct SFXTRE{
	struct beer{int fail,beg,len,son[27];}dot[n7*2];
	int cnt,rem,las,now;
	
	SFXTRE(){dot[0].len=inf,cnt=1,now=1;}

	int Dnew(int begz,int lenz){
		cnt++,dot[cnt]=(beer){1,begz,lenz};
		return cnt;
	}

	void isert(int id){
		rem++,las=1;
        //最长后缀长度加一，这一轮上一个被访问的节点显然是根节点
		while(rem){//当最长的，还在的后缀仍待清除
			while(rem>dot[ dot[now].son[ cr[id-rem+1] ] ].len){//当我可以走一条边的时候
				now=dot[now].son[ cr[id-rem+1] ];//走
				rem-=dot[now].len;//最长的后缀的长度减去
			}
			int &z=dot[now].son[ cr[id-rem+1] ];//我的下一个节点
			char ch=cr[ dot[z].beg+rem-1 ];//我的下一个边的最后一个字符（注意dot[i]的信息是【它连向父亲的边】的信息）
			if(!z||cr[id]==ch){//如果下一个节点还没有，或者我的当前后缀不存在
				dot[las].fail=now,las=now;//把fail连向现在（我的儿子的最长真后缀肯定是我）
				if(!z)z=Dnew(id,inf);//如果是没有下一个节点，就新增
				else return;//否则已经被隐式隐藏，就直接拜拜
			}			 
			else{//当前后缀在这个边出现，但不是完全覆盖（隐式）
				int fut=Dnew(dot[z].beg,rem-1);//新增出准备分裂的节点
				//注意，是把fut放在原来z的位置，z辈分更小一位
                dot[fut].son[ch]=z;//儿子是z
				dot[fut].son[ cr[id] ]=Dnew(id,inf);//另一个儿子是分裂出来的，新增
				dot[z].beg+=rem-1,dot[z].len-=rem-1;//更新z的信息
				z=fut,//now的儿子就是fut
                dot[las].fail=fut,//以前的fail就是fut
                las=fut;//fut变成上一个节点
			}
			if(now==1)rem--;//如果这个后缀已经给全部插入完，那就下一个
			else now=dot[now].fail;//否则就找到下一个应该插入的地方
		}
	}
}tre;