回文自动机PAM 学习笔记
这回不鸽了
思路
样子
abaaba
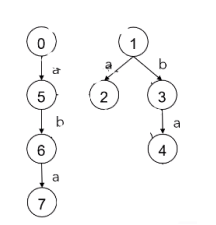
回文自动机 PAM 由两棵树组成。第一棵树根(偶根)的 \(len\) 为 0 ,代表着长为偶数的回文串;第二棵树根(奇根)的 \(len\) 为 -1,代表着长为奇数的回文串。注意:偶根代表的是空串,奇根无实际意义。
边代表的字母,表示它的回文串是“父亲节点对应的回文串”两边加上这个字母组成的串。例如,我代表的回文串是 'accbbcca',我有一条 'b' 边指向点 5 ,那么点 5 的回文串就是 'baccbbccab'。
所以如果有一个节点父亲是偶根,那么就相当于空串两边放上字母;如果有一个节点父亲是奇根,那么就相当于只放一个字母(可以这样理解:奇根串长 -1,两边加 'a' 就变成了长度为 1 的字符串 'a')。
构造
注意:回文串的最长回文后缀不包括它自己,即 'ababa' 的最长回文后缀是 'aba' 而不是 'ababa'。
一个节点的信息是这样的:
struct dino{int len,fail,to[26];}dot[m7];
len 就是这个点代表的回文串长度是多少,to[x] 代表这个点通过字母为 x 的边指向的儿子是谁,fail 是某个点最长回文后缀对应的 PAM 节点。
首先我们想想,假如我是第 \(i\) 位的字符,我想知道我可以拼哪个回文串(以哪个回文串为末尾)。那么,我看一下第 \((i-1)\) 位对应的回文串(假设是 \(cur\) )长度是 \(len\):
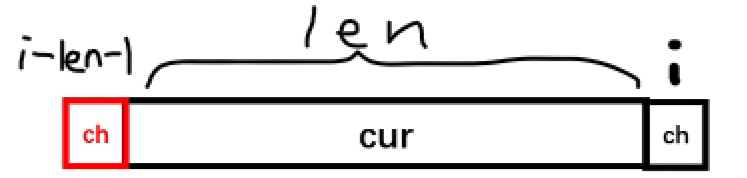
如果字符串第 \((i-len-1)\) 位和我一样,那我就知道我的字符串长度,以及我在 PAM 上的父亲等信息了!
但是不一样,怎么办呢?
这里有一个很巧妙的方法:走向 \(cur\) 的最长回文后缀。
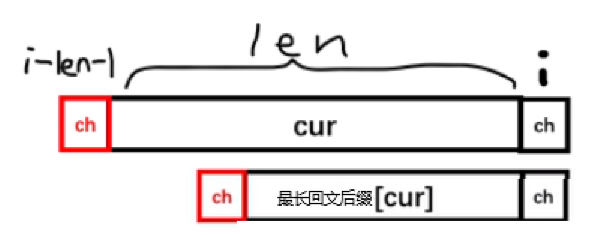
再次判断是否合法,还不一样就再跳:
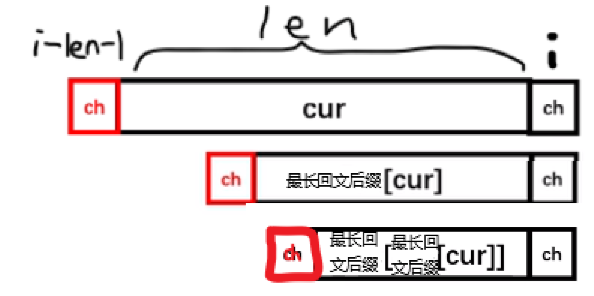
……
直到我们找到了合适的匹配,我将那个字符串对应的 PAM 节点作为我的父亲,\(len_{me}=len_{fa}+2\)。
跳后缀就相当于跳 \(fail\),所以代码也很好理解:
int Glegal(int z,int wei){//我左边那个位置的回文串长度为z,我是第 wei 位字符
while(cr[ wei-dot[z].len-1 ]^cr[wei])z=dot[z].fail;
//a^b 就是 a!=b 常数更小
return z;
}
如果一直找不到合法的,最后肯定会跳到奇根,奇根是一定合法的,所以不用担心。
所以初始化是这样的:
void plant(){
//注:第一位是len,第二位是fail
dot[0]=(dino){0,1};//偶根
dot[1]=(dino){-1,0};//奇根
//奇根的fail随便指,因为跳到它之后不会再跳fail了(但也不要乱指,建议指向0)
//初始化所有的fail都要指向偶根,因为偶根是有实际意义的空串
//而因为所有的fail都指向了0,所以把偶根设为0方便
}
那么我的 \(fail\) 是甚么呢?
因为现在 \(fa\) 对应字符串两边加上字符后就是我自己了,所以 \(fa\) 肯定不是我的 \(fail\) (最长回文后缀不能是自己),所以我的 \(fail\) 是 \(fail_{fa}\) 吗?
不一定,因为还要保证是回文串, \(fail_{fa}\) 没有保证第 \((i-len-1)\) 位字符和我一样。
于是我们还要不停跳,知道跳到合法为止。
所以代码就显然了:
void insert(int id){
int pre=Glegal(las,id);
if(!dot[pre].to[ cr[id] ]){
int tmp=Glegal(dot[pre].fail,id);
cnt++;
dot[cnt].len=dot[pre].len+2;
dot[cnt].fail=dot[tmp].to[ cr[id] ];
dot[pre].to[ cr[id] ]=cnt;
}
las=dot[pre].to[ cr[id] ];
}
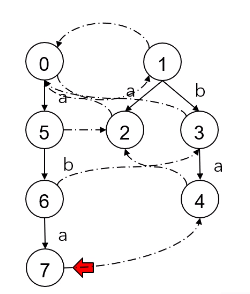
加了 \(fail\) 以后的 PAM (虚线就是 \(fail\) )
abaaba
总代码
加了一个 \(num\) ,假设第 \(i\) 位字符在 PAM 上对于节点为 \(P\),则 \(num_P\) 代表以 \(i\) 位置结尾的回文子串个数,转移也很显然 \(num_P=num_{fa}+1\)。
//SAM难死,还是PAM好贴贴
#include<bits/stdc++.h>
#define rep(i,x,y) for(int i=x;i<=y;++i)
using namespace std;
const int m7=501234;
struct dino{int len,fail,num,to[27];}dot[m7];
int n,cnt=1,las,cr[m7];char cz[m7];
void plant(){
dot[0]=(dino){0,1};//偶根
dot[1]=(dino){-1,0};//奇根
}
int Glegal(int z,int wei){
while(cr[ wei-dot[z].len-1 ]^cr[wei]){
z=dot[z].fail;
}
return z;
}
void insert(int id){
int pre=Glegal(las,id);
if(!dot[pre].to[ cr[id] ]){
int tmp=Glegal(dot[pre].fail,id);
cnt++;
dot[cnt].len=dot[pre].len+2;
dot[cnt].fail=dot[tmp].to[ cr[id] ];
dot[cnt].num=dot[ dot[cnt].fail ].num+1;
dot[pre].to[ cr[id] ]=cnt;
}
las=dot[pre].to[ cr[id] ];
}
int main(){
plant();
scanf("%s",cz+1);
n=strlen(cz+1);
int ans=0;
rep(i,1,n){
cz[i]=(cz[i]-97+ans)%26+97;
cr[i]=cz[i]-'a';
insert(i);
ans=dot[las].num;
printf("%d ",ans);
}
return 0;
}

