AC自动机 学习笔记
AC自动机问题
电光火石后,只见 \(n\) 个字符串 \(S\) 袭来,而你唯一能做的是,在你手上捧着的字符串 \(T\) 中,找到每个 \(S\) 各自出现了几次。
\(n\le 10^5,|T|,\sum|S|\le2\times10^6\)
简思路
思考一下 KMP,我们利用了字符串中子串的共同点,但是这里肯定是不行的,给每一个 \(S\) 构建 KMP 是 \(O(n^2)\) 的。
首先建一棵字典树 Trie,然后将 \(S_i\) 依次插入字典树中。
比如 \(S_1=abcd,S_2=bcf,T=abcflycakioi\),我们用 \(S_1\) 匹配到 \(T\) 的第 4 位,这时失配了,我们是否可以直接用 \(S_2\) 接着匹配?答案是肯定的。
我们设数组 \(fail_i\) 代表在 Trie 的 \(i\) 号节点上,如果失配了应该何去何从,跳到哪个节点继续匹配。
注意这里为了方便,Trie 的总统节点编号为 1。
比如 \(S_1=a,S_2=aa,S_3=ac,S_4=cb\),那么 Trie 是这样的:
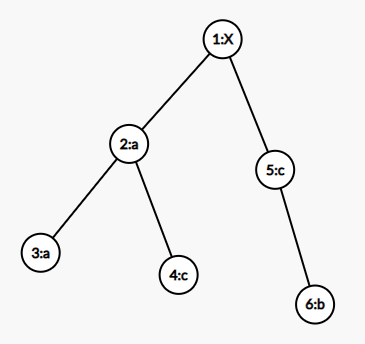
而加了 \(fail\) 是这样的(节点 \(i\) 用红色箭头指向 \(fail_i\))
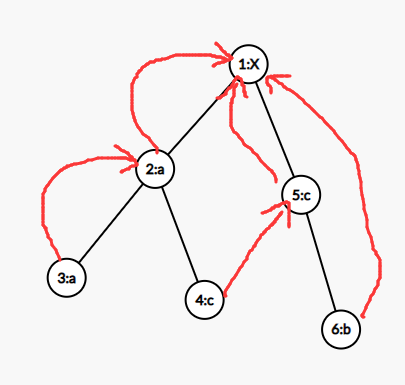
这样如果你匹配失败,就直接走向 \(fail\) 就行了!
注意,设根到点 \(i\) 的字符串是 \(A\),根到点 \(fail_i\) 的字符串是 \(B\) ,那么 \(B\) 是 \(A\) 的后缀。
代码实现
建树 - insert
首先建树。每输入完一个字符串 \(S\) 就按照字典树插入:
void insert(int z){
int len=strlen(cr+1),now=1;
rep(i,1,len){
int ch=cr[i]-'a';
if(!tre[now][ch]){
cnt++,tre[now][ch]=cnt;
}
now=tre[now][ch];
}
id[z]=now;//记录第z个字符串末尾是哪一个节点
}
求出fail - Gfail
然后就是求出 \(fail\) 了。我们用 bfs 实现。
首先,对于我这个节点,假设在 26 个儿子中,我枚举到了 'k'。
如果它存在,我的 'k'儿子的 \(fail\) 就是我的 \(fail\) 的儿子 'k'。这个不难理解,因为我的 \(fail\) 是我的后缀,和我差不多。然后把这个儿子的编号加入 bfs 队列。
否则,为了方便,我们直接让这个儿子指向(也就是编号变成)我的 \(fail\) 的儿子 'k',这样遍历就直接遍到那边去了。不加入 bfs 队列。但实际上这个儿子它还是不存在的。
void Gfail(){
head=1,tail=1,que[1]=1;
rep(i,0,25)tre[0][i]=1;//注释见下
while(head<=tail){
int now=que[head];
rep(i,0,25){
int edn=tre[ fail[now] ][i];
if(tre[now][i]){
fail[ tre[now][i] ]=edn;
edge(edn,tre[now][i]);
tail++,que[tail]=tre[now][i];
}
else tre[now][i]=edn;
}
head++;
}
}
注释:因为我们没有 0 号节点,所以我们把所有不存在的节点都指向 1,代表为了方便,遍历到这直接遍历回总统。但是这样做要把所有字典树节点都设为 1 ,显然不方便,我们就把 0 号点的儿子都指向 1,如果走到了 0,那么遍历 0 的儿子的时候就会回到 1。我只能赞叹:人类智慧!
查询 - query
这里就需要大脑跨越了。初始我们站在 Trie 中 1 号节点上,设 \(now\) 为我们的位置,则 \(now=1\)。当我们在检索到 \(T\) 的第 \(i\) 个字符时,如果它是 \(x\) ,则我们走到 \(now\) 的第 \(x\) 个儿子(即 \(now=tre[now][x]\)),然后我们开始跳 \(fail\):
因为一个字符串若匹配成功,那么它的 \(fail\) 也会匹配成功(是其后缀),它的 \(fail\) 的 \(fail\) 也会匹配成功(后缀的后缀还是后缀)……所以我们不停跳 \(fail\),让经过的点都加一。
因为 \(T\) 是跑着的(对于 \(T_i=x\) 每次走到 \(tre[now][x]\))所以肯定会匹配成功,直接加就完事了。
void query(){
int len=strlen(cr)-1,now=0;
rep(i,0,len){
now=tre[now][ cr[i]-'a' ];
int z=now;
while(z)tot[z]++,z=fail[z];
}
}
最后 \(S_i\) 成功匹配了 \(tot[\ id[i]\ ]\) 次!
这样就可以过 Luogu 模板题 弱化版 以及 正常版 了。
代码优化
显然这样一个一个加,时间太漫长。
如果 Trie 中点 \(o\) 被遍历到五次,每次都要加一,然后走去 \(fail\) 加一、 \(fail\) 的 \(fail\) 加一……这显然是不必要的。我们可以等到 \(T\) 匹配结束后,给 \(o\) 的 \(fail\) 以及 \(fail\ fail\)……加五,这样快了许多。
这就像一个拓扑图一样。于是整个 \(Gfail(\ )\) 结束后,我们把 Trie 当作拓扑图,\(\forall i\in \text{Trie},deg[\ fail[i]\ ]+1\)。这样做,就保证了正确传输。(即不会有 \(i\) 的 \(fail\) 加了 10 之后,又有 \(fail=i\) 的节点 \(j\) 给 \(i\) 权值加了 20 ,\(i\) 的 \(fail\) 又要加 20 这种情况)。
其它函数也要相应微调。
完整代码
#include<bits/stdc++.h>
#define rep(i,x,y) for(int i=x;i<=y;++i)
using namespace std;
const int n7=2012345;
struct dino{int son[27],fail;}tre[n7];
int n,cnt=1,idz[n7],tot[n7];
int head,tail,que[n7],deg[n7];char cr[n7];
int rd(){
int shu=0;char ch=getchar();
while(!isdigit(ch))ch=getchar();
while(isdigit(ch))shu=(shu<<1)+(shu<<3)+ch-'0',ch=getchar();
return shu;
}
void insert(int z){
int len=strlen(cr+1),now=1;
rep(i,1,len){
int tmp=cr[i]-'a'+1;
if(!tre[now].son[tmp]){
cnt++,tre[now].son[tmp]=cnt;
}
now=tre[now].son[tmp];
}
idz[z]=now;
}
void bfs(){
rep(i,1,26)tre[0].son[i]=1;
head=1,tail=1,que[1]=1;
while(head<=tail){
int now=que[head];
rep(i,1,26){
if(tre[now].son[i]){
tre[ tre[now].son[i] ].fail=tre[ tre[now].fail ].son[i];
deg[ tre[ tre[now].fail ].son[i] ]++;
tail++,que[tail]=tre[now].son[i];
}
else tre[now].son[i]=tre[ tre[now].fail ].son[i];
}
head++;
}
}
void query(){
int len=strlen(cr+1),now=1;
rep(i,1,len){
now=tre[now].son[ cr[i]-'a'+1 ];
tot[now]++;
}
}
void topo(){
head=1,tail=0;
rep(i,1,cnt){
if(!deg[i])tail++,que[tail]=i;
}
while(head<=tail){
int o=que[head];
tot[ tre[o].fail ]+=tot[o];
deg[ tre[o].fail ]--;
if(!deg[ tre[o].fail ])tail++,que[tail]=tre[o].fail;
head++;
}
}
int main(){
n=rd();
rep(i,1,n)scanf("%s",cr+1),insert(i);
bfs();
scanf("%s",cr+1);
query(),topo();
rep(i,1,n)printf("%d\n",tot[ idz[i] ]);
return 0;
}
杂题
Censor
维护两个栈,一个存 \(T\) 的点,一个存 Trie 的点。可以删的话,直接两个栈同时回退 \(l\) (删除的那个字符串的长度)个就好了。最后输出 \(stack-T\)(显然)。
Video Game
设 \(f_{i,j}\) 为长度为 \(i\) ,最后一个字符对应 Trie 上 \(j\) 号节点的最大匹配数。
转移显然:
void dp(){
memset(f,-0x3f,sizeof f),f[0][1]=0;
rep(i,0,m-1)rep(j,1,cnt)rep(k,0,2){
int tot=0,z=tre[j][k];
while(z)tot+=val[z],z=fail[z];
f[i+1][ tre[j][k] ]=max(f[i+1][ tre[j][k] ],f[i][j]+tot);
}
}
Fail 树
如果对于所有的字典树节点(当然不算那些事实上不存在的节点)连边 \(i-fail_i\),( 1 没有 \(fail\) ),就形成了一棵 Fail树 。
如果你想以 节点1 为根,可以连有向边 \(i\leftarrow fail_i\)。
Fail 树性质
所有 \(fail\) 直接或间接指向 \(i\) 号点的节点。都在 \(i\) 的子树中。
所以查询字符串 \(X\) 在字符串 \(Y\) 中出现几次,等价于建出 Trie 和 Fail树 后,在 Fail树中 以 “\(X\)的结束节点”(设为 \(i\)) 为根的子树中有多少个 \(Y\) 包含的节点。
不理解可以看这解释:比如 \(j\) 号点是 \(Y\) 所包含的,是 \(Y\) 的第 \(id\) 个节点,那么代表在 \(Y\) 查询时,\(j\) 跑 \(fail\) 可以跑出 \(X\),所以 \(X\) 是 \(Y\) 中 \(1\sim id\) 这个子串的后缀。
例题
阿机的打字狸
这就利用了上面的性质:Fail树上,我们只用知道把 \(Y\) 的点都加一后, \(X\) 结束节点子树的权值和就行了。
建 AC自动机、Fail 树,离线询问。
然后我们在 Trie 上 dfs,来到一个点在对应 Fail树 的点上权值加一,离开时减一。
如果来到了 \(i\) 节点,处理其挂着的所有询问(对于一询问 \(X,Y\),挂在 \(Y\) 上),查询 \(X\) 子树和。
问题变成:Fail树 上给某个点值,查询某个点子树和。这可以用dfs序实现。(因为dfs序中一个点的子树是连续的,变成了单点加和区间修,树状数组)。
Egovernment
与上题类似,让 \(T\) 在 Trie 上跑,经过的点对于的 Fail树 节点加一……但是然后我们要查询所有 \(S\) 的子树和,这显然炸了。
但是:给y的路径赋值,然后查询x的子树 等价于 给x的子树赋值,然后查询y的路径。
如法炮制,问题解决。

