论文解读（Polynormer）《Polynormer: Polynomial-Expressive Graph Transformer in Linear Time》

Note：[ wechat：Y466551 | 可加勿骚扰，付费咨询 ] 2024年4月14日17:13:41

论文信息

论文标题：Polynormer: Polynomial-Expressive Graph Transformer in Linear Time
论文作者：
论文来源：2024  aRxiv
论文地址：download
论文代码：download
视屏讲解：click

1-摘要

　　图转换器（GTs）已经成为一种很有前途的架构，它在理论上比消息传递图神经网络（GNNs）更具表现力。然而，典型的GT模型至少具有二次复杂度，因此不能扩展到大的图。虽然最近提出了一些线性GTs，但它们在几个流行的图数据集上仍然落后于GNN对应的数据集，这对它们的实际表达性提出了一个关键的关注。为了平衡GTs的表达性和可伸缩性之间的权衡，我们提出了多边形模型，一个具有线性复杂度的多项式表达性GT模型。多法线是建立在一个新的基础模型上，学习一个高度的多项式的输入特征。为了实现基模型的置换等变，我们将其与图拓扑和节点特征分别集成，得到局部和全局等变注意模型。因此，多法线采用线性局部到全局注意方案来学习系数由注意分数控制的高度等变多项式。多规范已经在13个亲同和异亲同数据集上进行了评估，包括具有数百万个节点的大图。我们广泛的实验结果表明，即使没有使用非线性激活函数，聚合在大多数数据集上也优于最先进的GNN和GT基线。

2-介绍

　　由于传统的图神经网络（GNNs）是建立在相邻节点之间交换信息的信息传递方案上的，已知它们会遭受过度平滑和过压压问题，导致它们对复杂函数的表达能力有限（近似）。受基于变压器的模型在语言和视觉领域的进步的启发，图变压器（GTs）近年来变得越来越流行，它允许节点关注图中的所有其他节点，并固有地克服了 GNN 的上述限制。特别是，Kreuzer 等人从理论上证明了具有无界层的 GTs 是图上通用的通用等变函数逼近器。然而，由于GT层的数量通常被限制在一个小的常量内，因此在实践中如何解锁GT的表达潜力仍不清楚。

　　在文献中，先前的一些研究试图通过位置编码（PE）和结构编码（SE）适当地涉及诱导偏倚来提高GT的表达能力。具体来说，Ying等人（2021）；Chen等人（2022a）；Zhao等人（2023）；Ma等人（2023）将几种SE方法与GT集成，以纳入关键结构信息，如节点中心性、最短路径距离和图子结构。此外，Kreuzer等人（2021年）；Dwivedi等人（2022年）；Rampasek等人（2022年）；Bo等人（2023年）介绍了基于拉普拉斯特征对的各种PE方法。尽管如此，这些方法通常涉及计算PE/SE的重要开销，并且大多采用普通变压器模型中的自注意模块，该模块对图中的节点数具有二次复杂度，禁止了它们在大规模节点分类任务中的应用。为了解决可伸缩性的挑战，最近提出了许多线性gt。具体而言，乔罗曼斯基等人（2021）；Zhang等人（2022）；Shirzad等人（2023）；Kong等人（2023）旨在通过利用节点采样或扩展图稀疏自注意矩阵，而Wu等人（2022；2023）关注基于核的自注意矩阵的近似。然而，之前的工作（Platonov et al.，2023）和我们的实证结果表明，这些线性GT模型在几个流行的数据集上仍然逊于最先进的GNN模型，这引起了人们对线性GT相对于GNN的实际优势的严重关注。

　　在这项工作中，我们提供了一种正交的方法来缓解GTs的表达性和可伸缩性之间的紧张关系。具体地说，我们提出了一种多法线，一种多项式表达的线性GT模型：l层多法线可以表示表示一个2L度的多项式，它将输入节点特征映射到输出节点表示，并且与节点排列等变。注意，多项式表达式很好地由维尔斯特拉斯定理激发，该定理保证任何光滑函数都可以用多项式近似（Stone，1948）。为此，我们首先引入一个基本注意模型，它显式地学习一个多项式函数，其系数由节点之间的注意分数决定。通过基于图拓扑和节点特征对多项式系数施加排列等方差约束，分别从基模型中推导出局部和全局注意模型。随后，多法采用了线性局部-全局注意范式来学习节点表示，这是语言和视觉领域高效转换器的常见做法，但在图上很少探索。为了证明多节点的有效性，我们进行了广泛的实验，将多节点与22个竞争性gnn和gt进行比较，这些数据集包括多达数百万个节点的同亲性和异亲性图。我们认为这可能是文献中最广泛的比较之一。我们的主要技术贡献总结如下：

• 据我们所知，我们是第一个提出一个多项式表达图转换器，这是通过引入一种新的注意模型来实现的，该模型明确地学习一个系数由注意分数控制的高度多项式函数。
• 通过将图的拓扑结构和节点特征分别积分到多项式系数中，我们导出了局部和全局的等变注意模块。因此，多法线利用局部到全局的注意机制来学习与节点排列等变的多项式。
• 由于高多项式表达率，没有任何激活函数的多法线能够在多个数据集上超过最先进的GNN和GT基线。当进一步与ReLU激活结合时，在13个节点，er中11个节点分类数据集中的11个比基线提高了4.06%的准确性，包括同源性和异亲性图。
• 通过规避密集注意矩阵的计算和现有技术中使用的昂贵的PE/SE方法，我们的局部到全局注意方案对于图的大小具有线性复杂度。这使得多形法线可伸缩到具有数百万个节点的大型图。

3-方法

3.1-高阶多项式

　　三阶多项式：

　　　　$ wx_{11}^3  + wx_{22}^3 + wx_{33}^3  +  wx_{11}^2  + wx_{22}^2 + wx_{33}^2  + w x_1 x_2 + wx_1 x_3 + wx_2 x_3 + wx_1 + wx_2+ wx_3 +b $

　　其中，权重 $w$ 不是共享的。

3.2-低阶表达能力和高阶表达能力

　　GNN 的消息传播方式（加权聚合）：

　　　　$\mathcal{P}(\boldsymbol{X})_{i}=\sum_{j} c_{i, j} \boldsymbol{X}_{j}$

　　其中，$c_{ij}$ 表示 节点 $i$ 和 节点 $j$ 之间的权重系数。

　　例子： [部分系数清0，则可得到下面 list 中的各项]

　　GNN

• • 对于两个节点的图：$\left[x_{1}, x_{2}, x_{1}+x_{2}\right]$
  • 对于三个节点的图：$\left[x_{1}, x_{2}, x_{3}, x_{1}+x_{2}, x_{1}+x_{3}, x_{2}+x_{3}, x_{1}+x_{2}+x_{3}\right]$

　　多项式：

• • 对于两个节点的图：$\left[x_{1}, x_{2}, x_{1}+x_{2}, x_{1} x_{2}\right]$
  • 对于三个节点的图：$\left[x_{1}, x_{2}, x_{3}, x_{1}+x_{2}, x_{1}+x_{3}, x_{2}+x_{3}, x_{1}+x_{2}+x_{3}, x_{1} x_{2}, x_{1} x_{3}, x_{2} x_{3}, x_{1} x_{2} x_{3}\right]$

3.3-多项式图模型

　　多项式模型可以表达为：

　　　　$\mathcal{P}(\boldsymbol{X})_{i}=\boldsymbol{X}_{i} \odot M^{r-1}$

　　其中，

• • $\boldsymbol{X} \in \mathbb{R}^{n \times d}$ 代表节点特征；
  • $\mathcal{P}: \mathbb{R}^{n \times d} \rightarrow \mathbb{R}^{n \times d}$ 代表多项式模型；
  • $\odot$ 代表 Hadamard product ；

　　举例：

　　多项式模型：

　　　　$\boldsymbol{y}=\mathcal{P}(\boldsymbol{x})=(\boldsymbol{W} \boldsymbol{x}) \odot(\boldsymbol{x}+\boldsymbol{b}) \quad (1)$

　　其中

• • $\boldsymbol{W} \in \mathbb{R}^{n \times n}$ ，$\boldsymbol{W}_{ij}$ 代表节点 $i$ 和 节点 $j$ 之间的注意力权重；
  • $\boldsymbol{b} \in \mathbb{R}^{n \times 1}$
  • $\boldsymbol{x} \in \mathbb{R}^{n\times 1}$ -> 每个节点为一标量值；

　　对于一个拥有三个节点的图来说：

　　

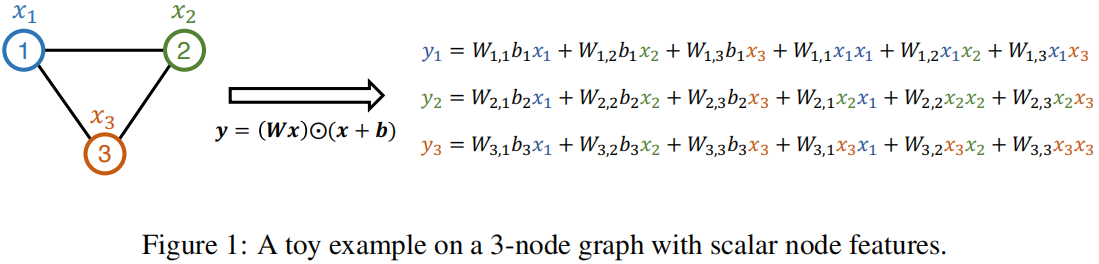
　　在 $\text{Eq.1} $ 中 ，$\boldsymbol{W} \boldsymbol{x}$ 产生低阶表达能力（局部注意力），而在其基础上添加 $\boldsymbol{x}+\boldsymbol{b}$ 则产生高阶表达能力（多项式）。

　　因此，对于节点特征为向量形式的，多项式模型为：

　　　　$\boldsymbol{X}^{(l)}=\left(\boldsymbol{W}^{(l)} \boldsymbol{X}^{(l-1)}\right) \odot\left(\boldsymbol{X}^{(l-1)}+\boldsymbol{B}^{(l)}\right) \quad(2)$

　　===>所以，已经可以推断出代码怎么写的了 [ $\text{GAT(}$$X_{l-1}$$\text{) }$+ $X_{l-1}$ ]

　　问题：虽然 多项式模型的表达能力提升了，但是由于 $\boldsymbol{W}$ 具有二次复杂度，所以不适合扩展到大图，因此在下文中提出了一个简化版本；

3.4-等变注意力多项式表达模型

模型框架

　　

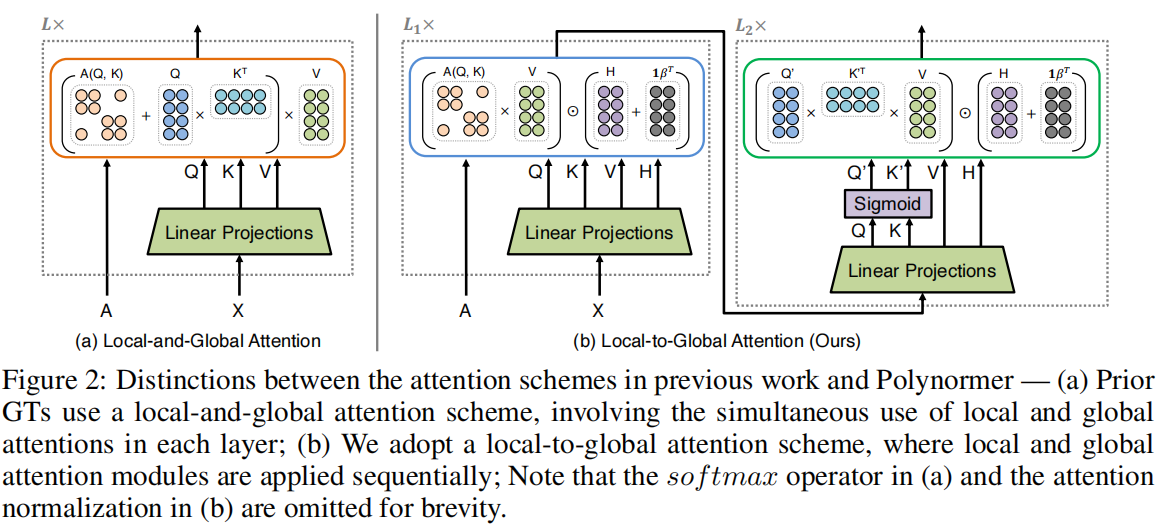
3.4.1 局部注意力模块

　　我们通过设置 $W = A$ 来合并图的拓扑信息，其中 $A$ 是一个稀疏注意矩阵，使 $A$ 中的非零元素表示相邻节点的注意分数。虽然 $A$ 可以通过采用先前提出的任何稀疏注意方法来实现，但我们选择了GAT注意方案：

　　　　$\boldsymbol{X}=\boldsymbol{A} \boldsymbol{V} \odot\left(\boldsymbol{H}+\sigma\left(\mathbf{1} \boldsymbol{\beta}^{\boldsymbol{T}}\right)\right) \quad(3)$

3.4.2 全局注意力模块

　　全局注意力：

　　　　$\boldsymbol{X}=\frac{\sigma(\boldsymbol{Q})\left(\sigma\left(\boldsymbol{K}^{T}\right) \boldsymbol{V}\right)}{\sigma(\boldsymbol{Q}) \sum_{i} \sigma\left(\boldsymbol{K}_{i,:}^{T}\right)} \odot\left(\boldsymbol{H}+\sigma\left(\mathbf{1} \boldsymbol{\beta}^{\boldsymbol{T}}\right)\right) \quad(4)$

4-实验

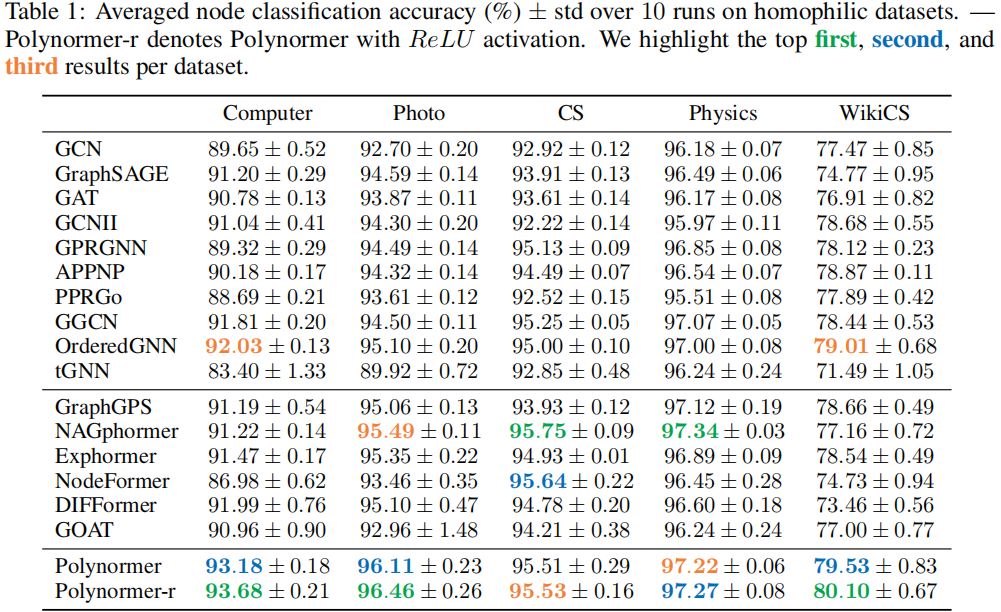
节点分类