论文解读（ACDNE）《Adversarial Deep Network Embedding for Cross-Network Node Classification》

Note：[ wechat：Y466551 | 可加勿骚扰，付费咨询 ]

论文信息

论文标题：Adversarial Deep Network Embedding for Cross-Network Node Classification
论文作者：Xiao Shen、Quanyu Dai、Fu-lai Chung、Wei Lu、Kup-Sze Choi
论文来源：2020 AAAI
论文地址：download 
论文代码：download
视屏讲解：click

1-摘要

　　本文研究了跨网络节点分类的任务，即利用源网络中丰富的标记节点来帮助对目标网络中的未标记节点进行分类。现有的领域自适应算法通常无法对网络结构信息进行建模，目前的网络嵌入模型主要集中在单网络应用上。因此，这两者都不能直接应用于解决跨网络节点分类问题。这促使我们提出了一种对抗性跨网络深度网络嵌入（ACDNE）模型，将对抗性域自适应与深度网络嵌入集成起来，从而学习网络不变节点表示，也可以很好地保留网络结构信息。在ACDNE中，深度网络嵌入模块利用两个特征提取器来共同保持节点之间的属性亲和力和拓扑邻近性。此外，还加入了一个节点分类器，使节点表示具有标签区分性。此外，还采用对抗域自适应技术使节点表示网络不变。大量的实验结果表明，该ACDNE模型在跨网络节点分类方面达到了最先进的性能。

2-介绍

　　贡献

1. ACDNE是第一个将深度网络嵌入与对抗域自适应集成起来，学习标签区分和网络不变表示的跨网络节点分类；
2. 所提出的深度网络嵌入模块有效地捕获了网络内节点和跨网络之间的拓扑邻近性和属性亲和力；
3. 在真实数据集中的大量实验结果验证了所提出的ACDNE模型对跨网络节点分类的有效性。

3-模型框架

　　

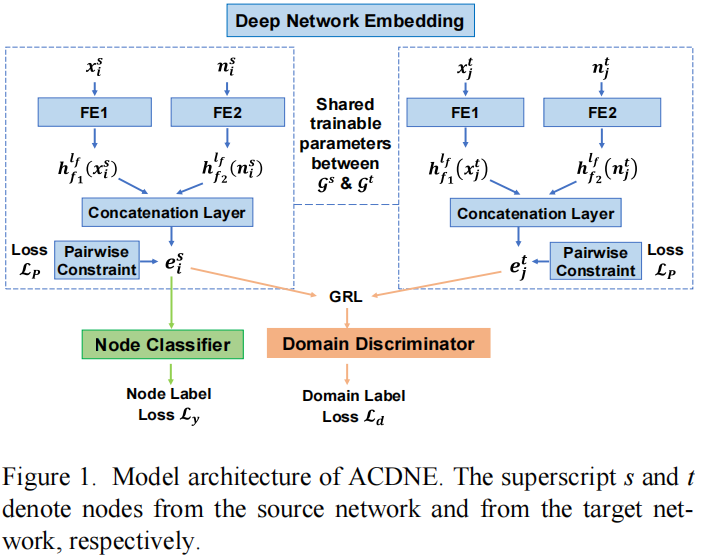
4-方法

4.1 深度节点表示学习

　　节点 $v_i$ 本身深度嵌入：

　　　　$h_{f_{1}}^{(k)}\left(x_{i}\right)=\operatorname{ReLU}\left(h_{f_{1}}^{(k-1)}\left(x_{i}\right) W_{f_{1}}^{(k)}+b_{f_{1}}^{(k)}\right), 1 \leq k \leq l_{f}\quad(1)$

　　节点 $v_i$ 邻域深度嵌入：

　　　　$h_{f_{2}}^{(k)}\left(n_{i}\right)=\operatorname{ReLU}\left(h_{f_{2}}^{(k-1)}\left(n_{i}\right) W_{f_{2}}^{(k)}+b_{f_{2}}^{(k)}\right), 1 \leq k \leq l_{f}\quad(2)$

　　领域定义【PPMI计算】：

　　　　$n_{i k}=\sum_{j=1, j \neq i}^{n} \frac{a_{i j}}{\sum_{g=1, g \neq i}^{n} a_{i g}} x_{j k}\quad(3)$

　　节点 $v_i$ 及其领域最终表示：

　　　　$e_{i}=\operatorname{ReLU}\left(\left[h_{f_{1}}^{\left(l_{f}\right)}\left(x_{i}\right), h_{f_{2}}^{\left(l_{f}\right)}\left(n_{i}\right)\right] W_{c}+b_{c}\right) \quad(4)$

4.2 成对约束

　　为了保持网络的拓扑近似性：

　　　　$\mathcal{L}_{p}=\frac{1}{n^{s}} \sum_{v_{i}, v_{j} \in V^{s}} a_{i j}\left\|e_{i}-e_{j}\right\|^{2}+\frac{1}{n^{t}} \sum_{v_{i}, v_{j} \in V^{t}} a_{i j}\left\|e_{i}-e_{j}\right\|^{2}\quad(5)$

4.3 节点分类

　　　　$\mathcal{L}_{y}=-\frac{1}{n^{s}} \sum_{v_{i} \in V^{s}} \sum_{k=1}^{c} y_{i k} \log \left(\hat{y}_{i k}\right)\quad(6)$

4.4 节点级对抗训练

　　　　$\mathcal{L}_{d}=-\frac{1}{n^{s}+n^{t}} \sum_{v_{i} \in\left\{V^{s} \cup V^{t}\right\}}\left(1-d_{i}\right) \log \left(1-\hat{d}_{i}\right)+d_{i} \log \left(\hat{d}_{i}\right)$