论文解读（CGC）《Generating Counterfactual Hard Negative Samples for Graph Contrastive Learning》

Note：[ wechat：Y466551 | 可加勿骚扰，付费咨询 ]

论文信息

论文标题：Generating Counterfactual Hard Negative Samples for Graph Contrastive Learning
论文作者：
论文来源：2023 WWW
论文地址：download 
论文代码：download
视屏讲解：click

0-摘要

　　图对比学习已经成为一种强大的无监督图表示学习工具。图对比学习成功的关键是获取高质量的正负样本作为对比对来学习输入图的底层结构语义。最近的工作通常是从同一训练批次中抽取正负样本或者从外部不相关的图中采样负样本。然而，这种策略存在一个明显的局限性：不可避免的采样到假负样本。本文提出了一种新颖的方法，利用反事实机制来生成用于图对比学习的难负样本。利用反事实机制来为图对比学习生成难负样本，可以确保生成的样本是相似的，但具有与正样本不同的标签。所提出的方法在多个数据集上取得了令人满意的结果，并且优于一些传统的无监督图学习方法和一些SOTA图对比学习方法。

1-介绍

　　图对比学习( GCL )已经成为无监督图表示学习的一种强有力的学习范式，其成功的关键在于从原始的输入图中生成高质量的对比样本。迄今为止，已经提出了各种生成正样本的方法，例如基于图增强的方法和多视图样本生成。尽管取得了不错的进展，尤其是在正样本对方面，但在负样本方面还远远不够。与对比学习中的正样本相比，负采样更具有挑战性。现有的负样本获取方法主要沿用传统的采样技术，这可能会引入不可察觉的假阴性样本。例如，图对比学从目标图所在的同一训练批次中采样其他图作为负样本。这种方法并不能保证采样得到的负样本图是真负例。为了减轻假负样本带来的影响，去偏处理被引入到图对比学习方法中。这些去偏图对比学习方法的思想是估计假负样本的概率。基于此，在对比学习阶段对一些置信度较低的负样本进行丢弃或者采用较低的权重处理这些负样本。尽管如此，图对比学习和基于去偏的变体方法仍然存在一个主要的限制，即采样策略大多是随机的，并不能保证采样得到的负样本对的质量。

　　高质量的负样本命名为难负样本。难负样本是与目标数据的标签不同的数据实例，其嵌入与目标数据的嵌入相似。考虑到前面讨论的基于采样策略的局限性，认为必须对生成过程施加严格的约束来保证生成负样本的质量( 即生成难负样本)。反事实推理是人类的一种基本推理模式，它帮助人们推理出哪些微小的行为变化可能导致最终事件结果的巨大差异。受反事实推理的启发，作者直观地想到，难负样本的生成应该是对目标图进行微小的改变，最终得到一个标签与原始图不同的扰动图。

　　本文提出一种反事实启发的生成式图对比学习方法，以获得难负样本。显式地引入约束条件，保证生成的负样本真实且为难样本，消除了目前图对比学习负样本获取方法中的随机因素。此外，一旦生成过程完成，也不需要进一步处理获得的样本(例如去偏)。

　　文章贡献如下：

• • 提出了一种新的自适应图扰动方法，CGC，可在图对比学习过程中产生高质量的难负样本；
  • 创新地将反事实机制引入图对比学习领域，利用其优势使生成的负样本既难又真。由于反事实机制在本项工作中的成功应用，进行反事实推理来解释图对比学习模型具有潜在的可行性；
  • 进行了大量的实验来证明该方法的有效性，与几种经典的图嵌入方法和一些新颖的图对比学习方法相比，该方法取得了最先进的性能；

2-方法

2.1 问题定义

　　给定图  $\mathcal{A}=\{\mathcal{V}, \mathcal{E}, \mathcal{X}\}$  ，其中  $\mathcal{V}$  表示所有节点，  $\mathcal{E}$  表示所有边，  $\mathcal{X}$  表示所有节点特征集实机制从原始输入图中生成负样本图。简单起见，本文只考虑两种难负样本图的生成，邻近扰动图  $\mathcal{A}^{\prime}=\left\{\mathcal{V}, \mathcal{E}^{\prime}, \mathcal{X}\right\}$  和特征掩码图  $\tilde{\mathcal{A}}=\{\mathcal{V}, \mathcal{E}, \tilde{\mathcal{X}}\}$  。定义

　　　　$\begin{array}{l}\underset{\mathcal{E}^{\prime}, \tilde{\mathcal{X}}}{\arg \max } \operatorname{sim}\left(\mathcal{A}, \mathcal{A}^{\prime}\right)+\operatorname{sim}(\mathcal{A}, \tilde{\mathcal{A}}) \\\underset{\mathcal{E}^{\prime}, \tilde{\mathcal{X}}}{\arg \max } D_{K L}\left(p(\mathcal{A}) \| p\left(\mathcal{A}^{\prime}\right)\right)+D_{K L}(p(\mathcal{A}) \| p(\tilde{\mathcal{A}}))\end{array}$

2.2 反事实自适应扰动

 

邻近扰动和特征掩码矩阵：

　　

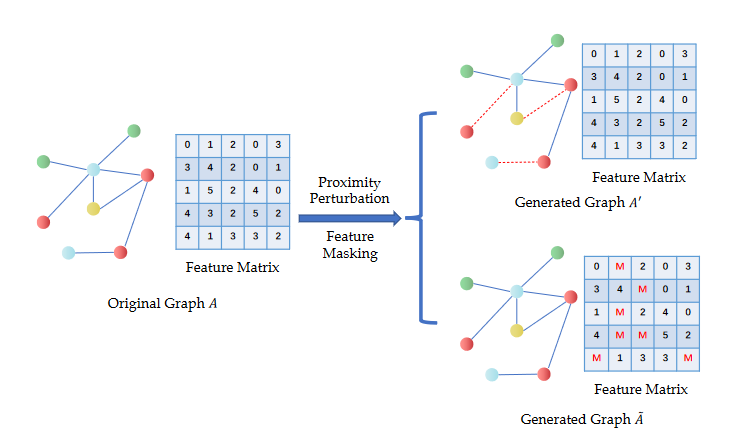
2.2.1 邻近扰动

　　$\mathrm{A}_{a}^{\prime}$  为扰动图的邻接矩阵，邻近扰动后获得邻近扰动图  $\mathcal{A}^{\prime}=\left\{\mathcal{V}, \mathcal{E}^{\prime}, \mathcal{X}\right\}$ 。

　　　　$\begin{array}{r}\mathrm{M}_{\boldsymbol{a}} \in \mathbb{R}^{\boldsymbol{N} \times \boldsymbol{N}} \\\mathrm{A} \in\{0,1\}^{N \times N} \\\mathrm{~A}_{a}=\mathrm{M}_{a} \times \mathrm{A} \\f: \mathrm{A}_{a} \in \mathbb{R}^{\boldsymbol{N} \times \boldsymbol{N}} \rightarrow \mathrm{A}_{a}^{\prime} \in\{0,1\}^{\boldsymbol{N} \times \boldsymbol{N}} \\\mathrm{A}_{a}^{\prime}=\mathbb{I}\left(\operatorname{sigmoid}\left(\mathrm{A}_{a}\right) \geq \omega\right)\end{array}$

2.2.2 特征掩码

　　$\tilde{\mathcal{X}}$ 为特征掩码图的特征矩阵，特征掩码后获得特征掩码图 $\tilde{\mathcal{A}}=\{\mathcal{V}, \mathcal{E}, \tilde{\mathcal{X}}\}$ 。

　　　　$\begin{array}{r}\mathbf{M}_{\boldsymbol{b}} \in \mathbb{R}^{\boldsymbol{N} \times \boldsymbol{h}} \\\mathcal{M}_{b}^{\prime}=\mathbb{I}\left(\operatorname{sigmoid}\left(\mathcal{M}_{b}\right) \geq \gamma\right) \\\tilde{\mathcal{X}}=\mathcal{M}_{b}^{\prime} \circ \mathcal{X}\end{array}$

2.2.3 扰动衡量

　　接下来要处理的问题是如何确保扰动后生成的两种类型的图是难负样本。利用反事实机制来解决这个问题，因为这种方法自然地满足了难负样本生成的要求。两者的目标都是输出语义层面不同但结构层面相似的东西。

　　首先讨论最大化原始图和扰动图之间的相似性，如下的目标函数试图确保所做的扰动尽可能小。

　　　　$\mathcal{L}_{s}=\left\|\mathrm{A}-\mathrm{A}_{a}^{\prime}\right\|_{F}-\left\|\mathrm{M}_{b}^{\prime}\right\|_{F}$

　　接下来，必须确保生成的图在语义层面上与原始图不同。考虑分类问题，最小化原始图和扰动图的类别概率分布之间的相似性。

　　　　$\mathcal{L}_{\mathcal{C}}=-D_{K L}\left(p(\mathcal{A}), p\left(\mathcal{A}^{\prime}\right)\right)-D_{K L}(p(\mathcal{A}), p(\tilde{\mathcal{A}}))$

　　用于生成难负样本的反事实预训练目标函数如下:

　　　　$\mathcal{L}_{\text {pre }}=\mathcal{L}_{s}+\mathcal{L}_{c}$

2.3 对比学习

　　采用反事实机制生成难负样本之后，需要对原始图和扰动图进行图对比学习。一个原始图和两个难负样本图，两个图编码器。公式如下，具体细节请参考原文。

　　　　$\mathcal{L}_{\text {contra }}=-\log \frac{\exp \left(\operatorname{sim}\left(\mathrm{q}, \mathrm{k}_{+}\right) / \tau\right)}{\sum_{t=0}^{|\mathcal{K}|-1} \exp \left(\operatorname{sim}\left(\mathrm{q}, \mathrm{k}_{t}\right) / \tau\right)}$

　　在完成基于反事实机制的难负样本生成和图对比学习两个训练阶段后，可以得到所有节点和图的训练嵌入。图嵌入将被输入到下游预测模型中进行图分类任务并评估训练好的嵌入的质量。

3 实验

3.1 数据集

数据集统计如下表，更多细节请参考原文。

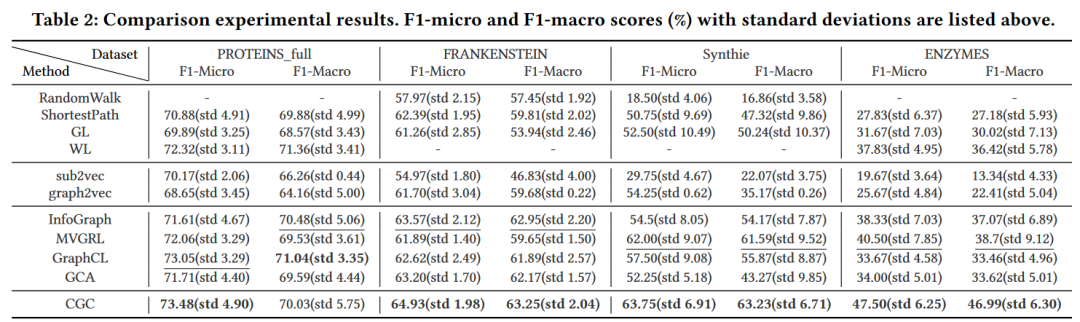
3.2 性能比较

　　对比实验结果如下图，更多细节请参考原文。

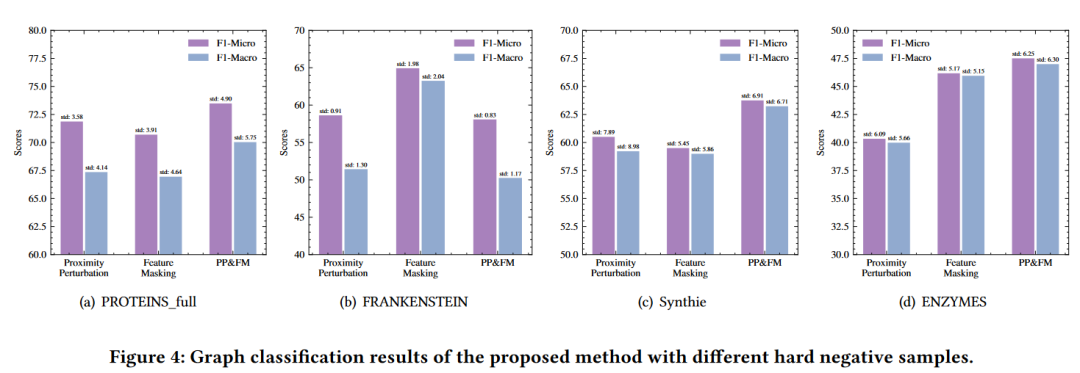
3.3 消融实验

• 生成的不同类型的难负样本对图对比学习的影响，实验结果如下图。

　　

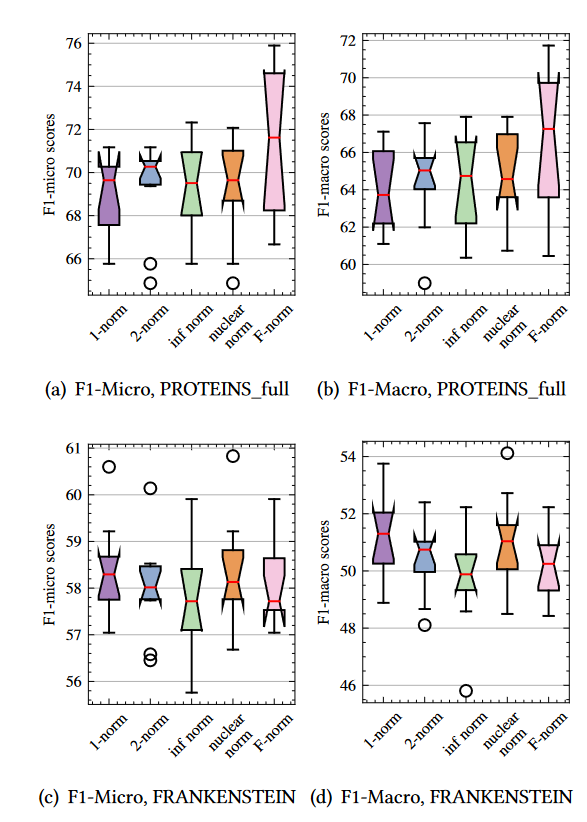
• 如何度量硬负样本生成过程中的相似性?即使用不同的范数对模型性能的影响，实验结果如下图。