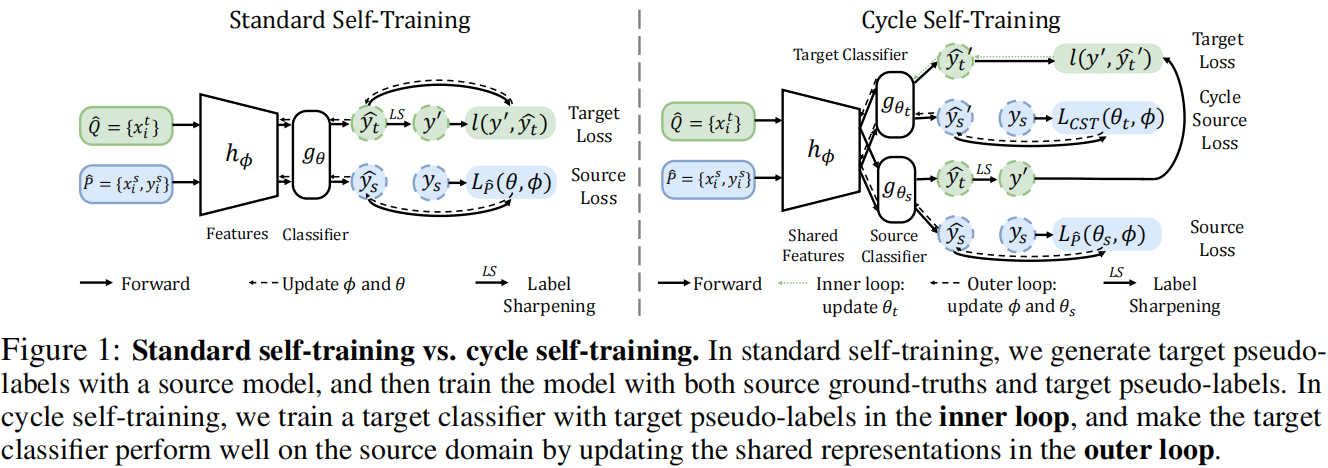
论文解读（CST）《Cycle Self-Training for Domain Adaptation》

Note：[ wechat：Y466551 | 可加勿骚扰，付费咨询 ]

论文信息

论文标题：Cycle Self-Training for Domain Adaptation
论文作者：Hong Liu, Jianmin Wang, Mingsheng Long
论文来源：2021 
论文地址：download 
论文代码：download
视屏讲解：click

1-介绍 

　　动机：在无分布偏移条件下，伪标签分布和真标签分布几乎相同，然而在有分布偏移条件下，两者差异很大。即使采用置信度、信息熵等不确定性阈值来筛选，筛选机制的可靠性仍将因为分布偏移而显著下降，最终使得标准自训练在领域自适应问题中失效。

2-相关

　　事实：分析了有无域位移的伪标签的质量，以更深入地研究UDA中标准自训练的难度。在流行的基准数据集上，当源和目标相同时，分析表明，伪标签分布与地面真实分布几乎相同。然而，由于分布位移，它们的差异可能非常大，有几个类大多被错误地分类为其他类。本文还研究了在域移下用流行标准选择正确伪标签的困难。虽然熵和置信度是没有域移的正确伪标签的合理选择标准，但域移使它们的精度急剧下降。

　　自训练和循环自训练：

　　

　　有或没有域移位的伪标签分布：

　　

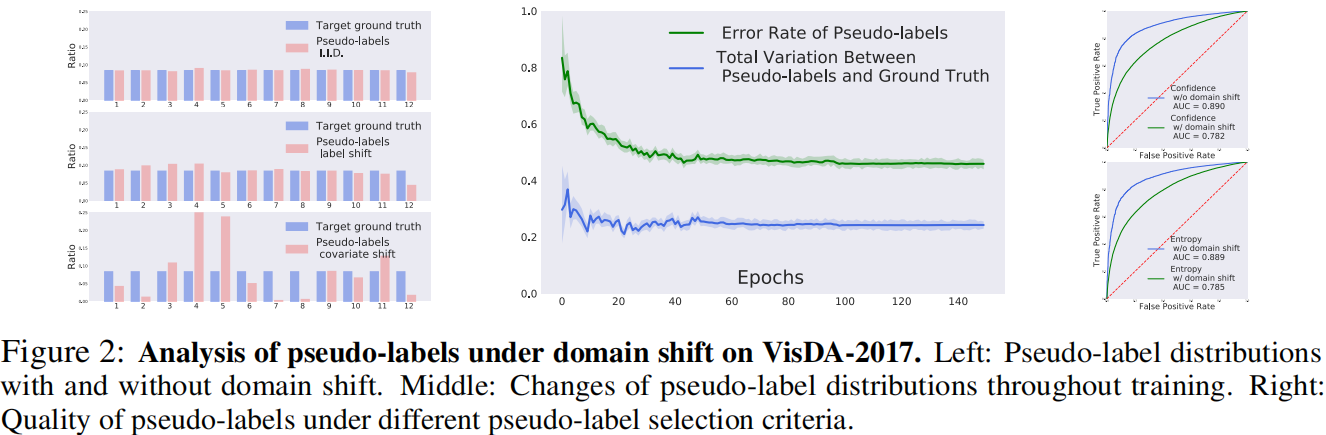
　　a）当源和目标分布相同时，伪标签的分布与地面真实分布相同，说明伪标签的可靠性。相反，当暴露在标签移位或协变量移位下时，伪标签的分布与目标的基本真实情况有显著的不同；

　　b）虽然伪标签的错误率继续下降，但 $d_{TV}$ 在整个训练过程中几乎保持不变，保持在 0.26。如果 $d_{TV}$ 收敛到 0.26，则伪标签的精度上限为 0.74，这说明在标准自训练中伪标签的重要去噪能力受到了域移的阻碍；

　　c）为了减轻虚假伪标签的负面影响，最近的研究提出了基于熵或置信准则[35,21,37,57]的阈值化来选择正确的伪标签。然而，目前尚不清楚这些策略在领域转移下是否仍然有效。在这里，比较了 3 种不同策略所选择的有无域转移的伪标签的质量。对于每种策略，计算不同阈值下的假阳性率和真阳性率，并绘制其ROC曲线；

3-方法

　　

Tsallis Entropy

　　　　$S_{\alpha}(y)=\frac{1}{\alpha-1}\left(1-\sum y_{[i]}^{\alpha}\right)$

def entropy(predictions: torch.Tensor, reduction='none') -> torch.Tensor:
    epsilon = 1e-5
    H = -predictions * torch.log(predictions + epsilon)
    H = H.sum(dim=1)
    if reduction == 'mean':
        return H.mean()
    else:
        return H

class TsallisEntropy(nn.Module):
    
    def __init__(self, temperature: float, alpha: float):
        super(TsallisEntropy, self).__init__()
        self.temperature = temperature  #2.0
        self.alpha = alpha  #1.9

    def forward(self, logits: torch.Tensor) -> torch.Tensor:
        N, C = logits.shape
        
        pred = F.softmax(logits / self.temperature, dim=1) 
        entropy_weight = entropy(pred).detach()
        entropy_weight = 1 + torch.exp(-entropy_weight)   #熵越大值越小
        entropy_weight = (N * entropy_weight / torch.sum(entropy_weight)).unsqueeze(dim=1)  
        
        sum_dim = torch.sum(pred * entropy_weight, dim = 0).unsqueeze(dim=0)  #torch.Size([1, C])

        result = 1 / (self.alpha - 1) * torch.sum((1 / torch.mean(sum_dim) - torch.sum(pred ** self.alpha / sum_dim * entropy_weight, dim = -1)))
        return result