论文解读(CTDA)《Contrastive transformer based domain adaptation for multi-source cross-domain sentiment classification》
Note:[ wechat:Y466551 | 可加勿骚扰,付费咨询 ]
论文信息
论文标题:Contrastive transformer based domain adaptation for multi-source cross-domain sentiment classification
论文作者:Yanping Fu, Yun Liu
论文来源:2021 aRxiv
论文地址:download
论文代码:download
视屏讲解:click
1 介绍
动机:传统的域自适应方法侧重于减少源域和目标域之间的域差异,但忽略了有效源的选择,无法处理负转移,导致性能有限;
方法:
-
- 设计一个混合选择器权重所有相关来源或挑选出Top-K来源根据两个领域之间的空间相似性;
- 构建一个适配器提取域不变的特性的信息通过最小化两个领域之间的瓦瑟斯坦距离;
- 构造一个鉴别器捕获的域私人信息特征对比学习;
- 执行加权分类器根据多个训练的源分类器预测目标域的情绪趋势;
贡献:
-
- 提出了一种混合多源域选择策略来对所有相关源进行加权或选择 Top-K 源,它选择相关源,消除无关源或恶意源,以减少负传递的影响;
- 提出了一种域适配器和鉴别器来自动捕获包含域共享和域私有信息的特征,从而最好地支持实现跨域自适应的最终预测;
- 提出了一种新的加权策略来聚合多个源分类器来构建一个情绪预测器,它可以强调不同源域的重要性;
- 在FDU-MTL和Amazon审查数据集上进行了广泛的实验,结果表明我们的CTDA框架可以在无监督的MCSC任务上实现显著的性能;
2 相关知识
-
- 由来自不同域的数据引起的域偏移;
- 在消除域差异时保留域私有特征;
- 负迁移问题;
思路:
-
- 通过生成域不变和域私有特征[8,9]来构建情绪分类器;
- 利用域自适应方法来弥补域的差距;
Note:共享私有模型,特征空间被划分为共享空间还是私有空间,主要取决于这些词在统计上是否相同。随后,通过应用深度神经网络将 pivot 和 non-pivots 提取为域共享和域私有特征。然而,这些方法也存在一些问题,如域不变特征,包括一些无关的域私有特征,共享的域特征被划分为私有空间,它们削弱了情绪分类器在 UCSC 任务中的识别能力。
多源域情感分类存在的问题:
-
- ① 如何从多个源域中选择合适的来源,以及如何对所选的来源进行加权,以获得有效的情绪传递。传统的策略是直接结合所有源域的知识,将其转移到目标域。然而,无关源或恶意源会对 MCSC 任务的性能产生负面影响;
- ② 如何将多个源域的知识转移到目标域?目前还没有合适的方案来平衡域自适应和域私有信息;
3 方法
整体框架:
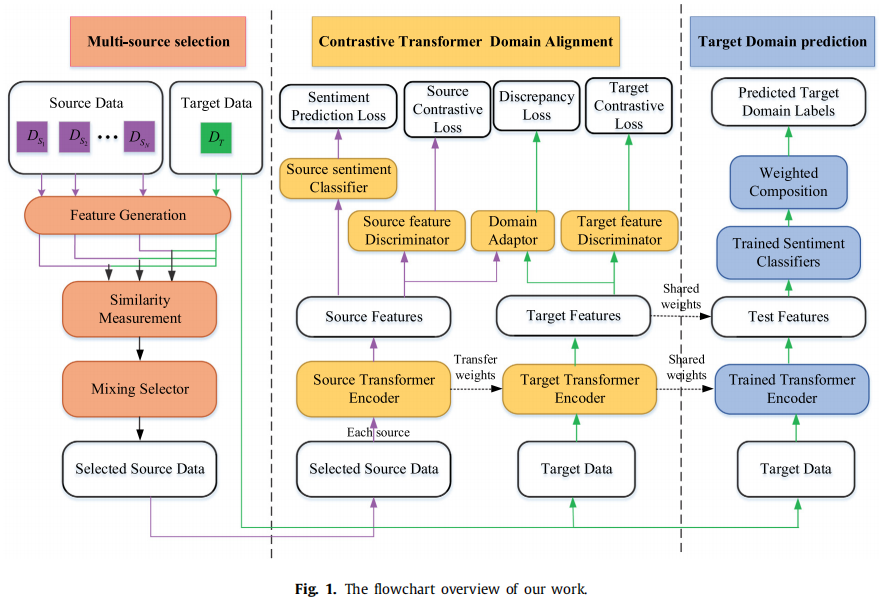
3.1 多源选择策略
框架
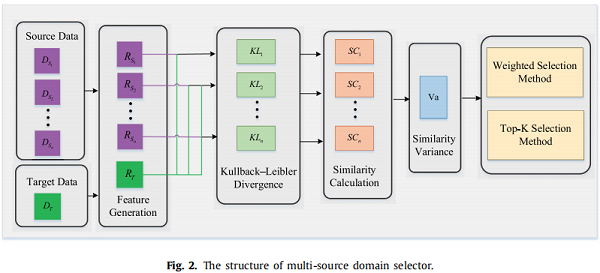
特征提取:
$R_{S_{i}}=\operatorname{BERT}\left(X_{S_{i}}\right) $
$R_{T}=\operatorname{BERT}\left(X_{T}\right)$
计算每个源域和目标域特征之间的 KL 散度来评估域相似性:
$K L_{i}=K L\left(g_{S_{i}} \| g_{T}\right)+K L\left(g_{T} \| g_{S_{i}}\right)$
其中:
$g_{S_{i}}=\exp \left(\operatorname{norm}\left(g_{S_{i}}^{\prime}\right)\right), \quad g_{S_{i}}^{\prime}=\frac{1}{n_{S_{i}}} \sum_{k=1}^{n_{S_{i}}} R_{S_{i}}(k)$
$g_{T}=\exp \left(\operatorname{norm}\left(g_{T}^{\prime}\right)\right), \quad g_{T}^{\prime}=\frac{1}{n_{T}} \sum_{k=1}^{n_{T}} R_{T}(k)$
Note:$\text{norm}$ 为 $\text{l2}$ 归一化操作,$k$ 表示第 $i$ 个源域中的第 $k$ 个样本;
相似性得分如下:
$S C_{i}=\beta K L_{i}$
受 [44] 启发,多源选择器依赖于 “ 特征分布距离越近,实例越相关 ” 的理论。根据相似度方差提出了一种混合选择策略,其计算方法如下:
$V a^{2}=\frac{\sum_{i=1}^{N}\left(S C_{i}-M\right)^{2}}{N}$
式中,$\text{M}$ 为相似度得分的平均值,$\text{N}$ 为源域的个数;
在得到相似性方差之后,混合选择策略包括如下两种方案:
-
- 加权选择方法;
- Top-K 选择方法;
加权选择方法
选择:当相似度方差较小时,不同对源域和目标域之间的分布差异波动较小。即 所有的源域和目标域几乎都位于同一相似性级别上,所以可以利用所有源的知识来预测目标域;
由于每个源域的知识转移的贡献是不同的,目标域的边际分布是所有源域加权和,每个源的权值表示为 $\alpha_{s_{i}}$,加权方法如下:
$P_{T}=\sum_{i=1}^{n_{S_{i}}} \alpha_{S_{i}} P\left(X_{S_{i}}\right)$
其中:
$\alpha_{S_{i}}=\frac{S C_{i}}{\sum_{i=1}^{n_{S_{i}}} S C_{i}}$
注意:$P\left(X_{S_{i}}\right)$ 表示第 $i$ 个源预测器预测的目标域的边际分布,$P_{T}$ 表示目标域的最终边际分布;
选择:当相似度方差较大时,不同源域和目标域之间的分布差异较大。即 只有部分域对之间的分布差异较小,而其他域之间的分布差异较大;
基于这个假设,选择与目标域 $\text{Top-K}$ 相关的源域作为可转移域,来消除其他源域以减少负转移。边际分布的计算过程与加权选择方法相同。
3.2 域对齐
框架
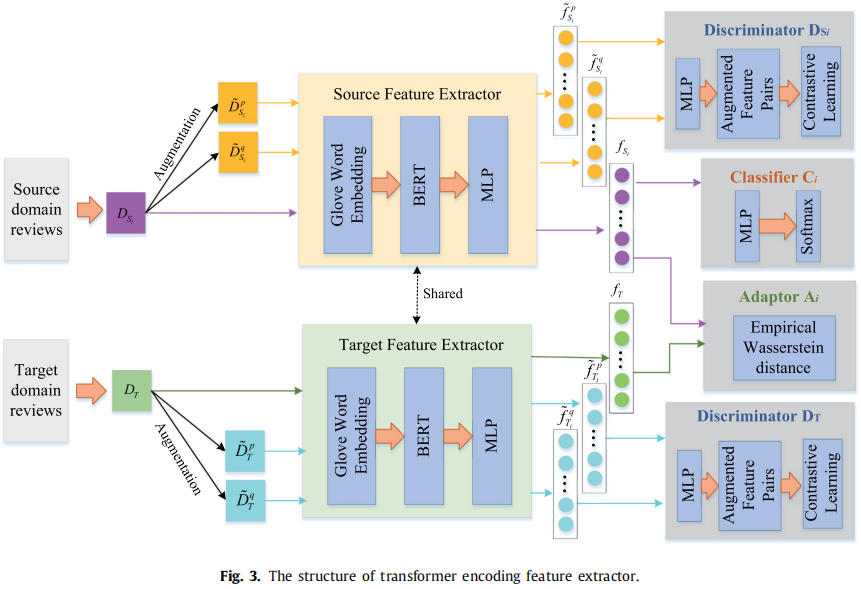
一对源域和目标域包含的组件:
-
- 共享的 Feature extractor
- 一个 Domain adaptor
- 两个 Domain discriminator
- 一个 Sentiment classifier
Feature extractor
$w_{S_{i}}(k)=\operatorname{Glove}\left(x_{S_{i}}(k)\right)$
$b_{S_{i}}(k)=B E R T\left(w_{S_{i}}(k)\right)$
$f_{S_{i}}(k)=A b_{S_{i}}(k)+c$
Domain adaptor
该小结参考 《Wasserstein Distance Guided Representation Learning for Domain Adaptation》----作者该小结完全抄袭,并没有引用;
目的:通过减少域差异(域对齐)来消除域偏移;
策略:对抗性训练;
文档特征 $f_{S_{i}}$ 和 $f_{T}$,瓦瑟斯坦距离:
$W_{a}\left(f_{S_{i}}, f_{T}\right)=\underset{\left\|f_{w}\right\|_{L\le 1}}{\text{sup}} E_{f_{s_{i}}}\left[f_{w}\left(f_{S_{i}}\right)\right]-E_{f_{T}}\left[f_{w}\left(f_{T}\right)\right]$
其中,$f_{w}$ 是满足 1-Lipschitz 约束 的特征映射函数,参数为 $θ_w$;
域差异 $L_{wf}$:
$L_{w f}\left(f_{S_{i}}, f_{T}\right)=\frac{1}{n_{S_{i}}} \sum_{f_{S_{i}} \in D_{S_{i}}} f_{w}\left(f_{S_{i}}\right)-\frac{1}{n_{t}} \sum_{f_{T} \in D_{t}} f_{w}\left(f_{t}\right)$
$fw$ 需满足 Lipschitz 约束,提出梯度惩罚函数 $L_{wg}$:
$L_{w g}\left(f_{S_{i}}, f_{T}\right)=\left\|\nabla_{\hat{d}} f_{w f}(\hat{d})\right\|-1$
Domain adaptor 训练目标:
$L_{w}= \underset{\theta_{w}}{\text{max}} \;\;\left\{L_{w f}\left(f_{S_{i}}, f_{T}\right)-\lambda \cdot L_{w g}\left(f_{S_{i}}, f_{T}\right)\right\}$
Feature extractor 训练目标:
$\underset{W_{a}}{\text{min}}\;\left(\theta_{e}\right)=\underset{\theta_{e}}{\text{min}} L_{w}$
框架
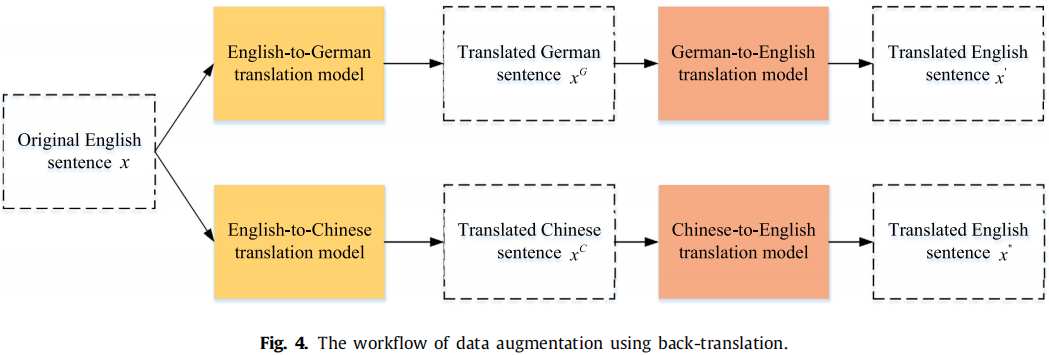
目的:域对齐过程中,在捕获域共享特性时可能导致域私有信息的丢失,因此本节用对比学习方法来保留域私有特征;
对比损失:
$l(p, q)=-\log \frac{\exp \left(\operatorname{sim}\left(\tilde{S_{S_{i}}^{p}}, \tilde{S_{S_{i}}^{q}}\right) / \delta\right)}{\sum_{j=1}^{2 M} \mathbb{I}_{[j \neq p]} \exp \left(\operatorname{sim}\left(\tilde{f}_{S_{i}}^{p}, \tilde{f}_{S_{i}}^{j}\right) / \delta\right)}$
源域的 $\tilde{f}_{S_{i}}^{p}$,$\tilde{f}_{S_{i}}^{q}$ 的正对是一致的,但负对是不同的,对称的对比损失函数为:
$L_{\text {con }}^{f_{i}}=\frac{1}{2 M} \sum_{k=1}^{M}[l(p(k), q(k))+I(q(k), p(k))]$
源域和目标域的对比损失:
$L_{c o n}=L_{c o n}^{s_{i}}+L_{c o n}^{T}$
情绪分类器是一层的 MLP ,源域情绪损失如下:
$L_{\text {sent }}=-\frac{1}{n_{s_{i}}} \sum_{k=1}^{n_{s_{i}}} y_{s_{i}}^{P}(k) \ln \left(y_{S_{i}}^{t}(k)\right)+\left(1-y_{s_{i}}^{p}(k)\right)\left(1-\ln \left(y_{S_{i}}^{t}(k)\right)\right)$
其中,$y_{S_{i}}^{t}(k)$ 表示情绪标签;
3.3 联合训练
训练目标:
$L_{\text {totle }}=\sum_{j=1}^{\hat{N}} L_{\text {totle }}^{j}=\sum_{j=1}^{\hat{N}}\left(\sigma L_{W_{a}}^{j}+\tau L_{\text {con }}^{j}+L_{\text {sent }}^{j}\right)$
其中,$\hat{N}$ 表示多源选择策略决定的源域数量;
算法:

3.4 加权预测
假设所选择的有效源域数为 $N$,使用不同的分类器加权预测:
$C_{T}=\sum_{j=1}^{N} \alpha_{S_{i}} C_{T}^{j}\left(f_{T}^{j}\right)$
第 $i$ 个源和目标之间的瓦瑟斯坦距离 $L_{W i}$,权值 $\alpha_{S_{i}}$ 计算如下:
$\alpha_{S_{i}}=\frac{e \frac{-L_{W i}^{2}}{2}}{\sum_{i=1}^{n_{S_{i}}} e \frac{-L_{W i}^{2}}{2}}$
4 实验
实验关注的问题:
-
- 混合选择策略能解决负转移问题吗?
- CTDA能否捕获包括域共享和域私有信息在内的特性,并获得比基线实验更好的性能?
- 分类器加权分量的建议是否有效?
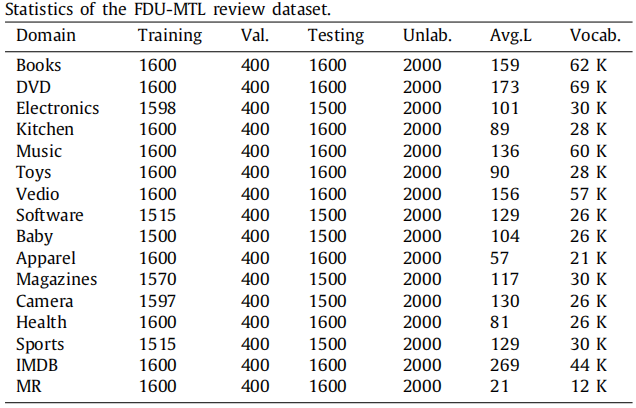
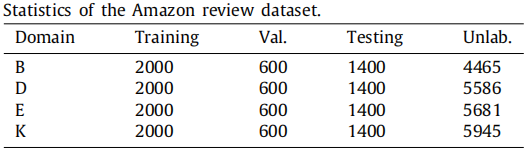
数据集
多源选择策略的效果
FDU-MTL数据集包括16个域,有足够的源来允许选择不同的策略,只在 FDU-MTL数据集上进行了实验,以验证多源选择策略,两个域之间的 KL 散度越小,其相似性越高;
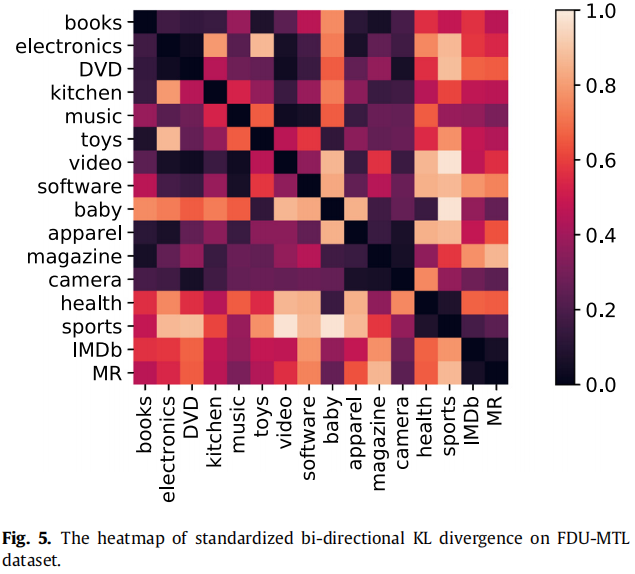
根据相似性方差选择源域和目标域:数量级为 0.1 的采用 Top-K 选择方法,数量级为 0.01 的全部选择;
![]()
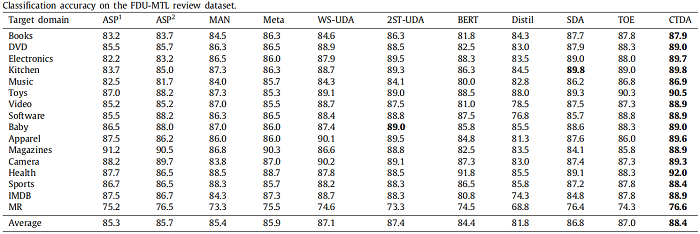

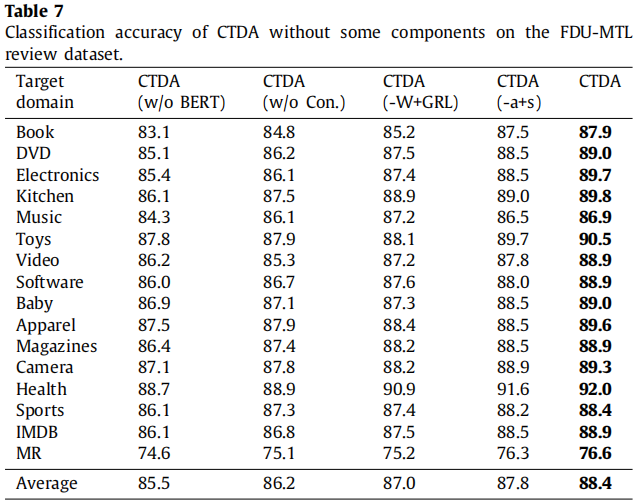
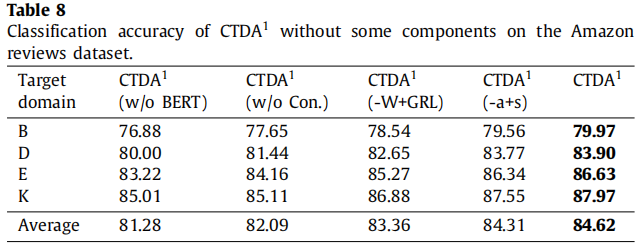
消融实验
因上求缘,果上努力~~~~ 作者:图神经网络,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/17638890.html


