论文解读（TAT）《 Transferable Adversarial Training: A General Approach to Adapting Deep Classifiers》

Note：[ wechat：Y466551 | 可加勿骚扰，付费咨询 ]

论文信息

论文标题：Transferable Adversarial Training: A General Approach to Adapting Deep Classifiers
论文作者：Hong Liu, Mingsheng Long, Jianmin Wang, Michael I. Jordan
论文来源：ICML 2019
论文地址：download 
论文代码：download 

1 Introduction

　　出发点：当使用对抗性训练的时候，因为抑制领域特定的变化时，会扭曲原始的特征分布；

　　事实：

　　

　　Figure2(b)：

• • 对比对抗性训练（DANN、MCD）和监督训练（EestNet50）在源域和目标域上的测试误差；
  • 结论：使用对抗性训练，减少特定领域的变化打破了原始表示的判别结构；

　　Figure2(c)：

• • 计算特征表示层模型权重的奇异值分布；
  • 结论：使用对抗性训练的奇异值分布更加重尾，表示产生了扭曲的特征表示；

2 方法

2.1 模型框架

　　

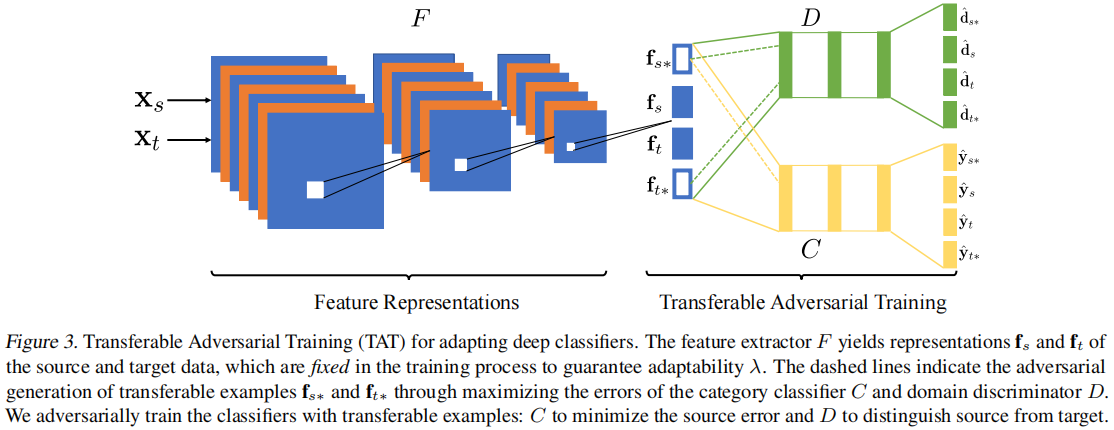
2.2 Adversarial Generation of Transferable Examples

　　域鉴别器 $D$ 训练目标：

　　　　$\begin{aligned}\ell_{d}\left(\theta_{D}, \mathbf{f}\right)= & -\frac{1}{n_{s}} \sum_{i=1}^{n_{s}} \log \left[D\left(\mathbf{f}_{s}^{(i)}\right)\right] -\frac{1}{n_{t}} \sum_{i=1}^{n_{t}} \log \left[1-D\left(\mathbf{f}_{t}^{(i)}\right)\right] \end{aligned}   \quad\quad(1)$

　　分类器 $C$ 训练目标：

　　　　$\ell_{c}\left(\theta_{C}, \mathbf{f}\right)=\frac{1}{n_{s}} \sum_{i=1}^{n_{s}} \ell_{c e}\left(C\left(\mathbf{f}_{s}^{(i)}\right), \mathbf{y}_{s}^{(i)}\right) \quad\quad(2)$

　　本文通过一种新的对抗性训练范式生成的可转移样本来填补源域和目标域之间的差距，从而减少分布变化。

　　生成的可转移样本需要满足两个条件：

• • 首先，可转移的样本应该有效地混淆域鉴别器 $D$，从而填补域间隙，桥接源域和目标域；
  • 其次，可转移的样本应该能够欺骗类别分类器 $C$，这样它们就可以推动决策边界远离数据点；

　　因此，可转移的样本是通过 $\ell_{c}$ 和 $\ell_{d}$ 的联合损失而反向生成的：

　　　　$\begin{aligned}\mathbf{f}_{t^{k+1}} \leftarrow \mathbf{f}_{t^{k}} & +\beta \nabla_{\mathbf{f}_{t^{k}}} \ell_{d}\left(\theta_{D}, \mathbf{f}_{t^{k}}\right) \\& -\gamma \nabla_{\mathbf{f}_{t^{k}}} \ell_{2}\left(\mathbf{f}_{t^{k}}, \mathbf{f}_{t^{0}}\right) \\\end{aligned} \quad\quad(3)$

　　　　$\begin{aligned}\mathbf{f}_{s^{k+1}} \leftarrow \mathbf{f}_{s^{k}} & +\beta \nabla_{\mathbf{f}_{s}} \ell_{d}\left(\theta_{D}, \mathbf{f}_{s^{k}}\right) \\& -\gamma \nabla_{\mathbf{f}_{s}} \ell_{2}\left(\mathbf{f}_{s^{k}}, \mathbf{f}_{s^{0}}\right) \\& +\beta \nabla_{\mathbf{f}_{s k}} \ell_{c}\left(\theta_{C}, \mathbf{f}_{s^{k}}\right)\end{aligned} \quad\quad(4)$

　　其中，$\mathbf{f}_{t^{0}}=\mathbf{f}_{t}, \mathbf{f}_{s^{0}}=\mathbf{f}_{s}, \mathbf{f}_{t *}=\mathbf{f}_{t^{K}}, \mathbf{f}_{s *}=\mathbf{f}_{s^{K}}$。

　　即：

• • 域分类损失最大化；
  • 距离最小化；
  • 分类损失最大化；

　　注意：为避免生成的样本的发散，控制生成的样本与原始样本之间的 $\ell_{2} \text{distance}$；

2.3 Adversarial Training with Transferable Examples

　　分类器 $C$ 的对抗性训练的损失函数如下：
　　　　$\begin{aligned}\ell_{c, a d v}\left(\theta_{C}, \mathbf{f}_{*}\right) & =\frac{1}{n_{s}} \sum_{i=1}^{n_{s}} \ell_{c e}\left(C\left(\mathbf{f}_{s *}^{(i)}\right), \mathbf{y}_{s *}^{(i)}\right)  +\frac{1}{n_{t}} \sum_{i=1}^{n_{t}}\left|C\left(\left(\mathbf{f}_{t *}^{(i)}\right)\right)-C\left(\left(\mathbf{f}_{t}^{(i)}\right)\right)\right|\end{aligned} \quad\quad(5)$

　　作用：可转移的样本训练分类器提高了分类器对 对抗性扰动 和 域变化 的鲁棒性；

　　域鉴别器 $D$ 的对抗性训练的损失函数如下：

　　　　$\begin{aligned}\ell_{d, a d v}\left(\theta_{D}, \mathbf{f}_{*}\right)= & -\frac{1}{n_{s}} \sum_{i=1}^{n_{s}} \log \left[D\left(\mathbf{f}_{s *}^{(i)}\right)\right] -\frac{1}{n_{t}} \sum_{i=1}^{n_{t}} \log \left[1-D\left(\mathbf{f}_{t *}^{(i)}\right)\right]\end{aligned} \quad\quad(6)$

　　作用：稳定对抗性训练，并弥合领域上的差异；

　　最小化  $\text{Eq.1}$ 和 $\text{Eq.6}$ 来训练 $D$，最小化 $\text{Eq.2}$ 和 $\text{Eq.5}$ 来训练 $C$，训练目标：

　　　　$\begin{array}{l}\underset{\theta_{D}, \theta_{C}}{\text{min}}\;\;\ell_{d}\left(\theta_{D}, \mathbf{f}\right)+\ell_{c}\left(\theta_{C}, \mathbf{f}\right) +\ell_{d, a d v}\left(\theta_{D}, \mathbf{f}_{*}\right)+\ell_{c, a d v}\left(\theta_{C}, \mathbf{f}_{*}\right) \end{array} \quad\quad(7)$

3 实验