论文解读(AAD)《Knowledge distillation for BERT unsupervised domain adaptation》
Note:[ wechat:Y466551 | 可加勿骚扰,付费咨询 ]
论文信息
论文标题:Knowledge distillation for BERT unsupervised domain adaptation
论文作者:Minho Ryu、Geonseok Lee、Kichun Lee
论文来源:2022 aRxiv
论文地址:download
论文代码:download
视屏讲解:click
1 介绍
出发点:域偏移导致的性能下降;
问题定义:UDA
比较有意思,这篇工作被抄袭了,但是抄袭的家伙还成功发论文了.............
知识蒸馏
启发点:标准的监督训练,由于使用的是硬标签做监督训练,所以在重复训练的时候容易造成过拟合。由于较大的 $t$ 值产生较软的概率分布,知识蒸馏在结合领域自适应方法可以缓解这一问题。
知识蒸馏 [7,8](KD)最初是一种模型压缩技术,旨在训练一个紧凑的模型(学生),以便将一个训练良好的更大的模型(教师)的知识转移到学生模型[28,29]。KD 可以通过最小化以下目标函数来表示:
$\mathcal{L}_{K D}=t^{2} \sum_{k}-\operatorname{softmax}\left(p_{k}^{T} / t\right) \times \log \left(\operatorname{softmax}\left(p_{k}^{S} / t\right)\right)$
其中,$p^{S}$ 和 $p^{T}$ 分别为学生模型和教师模型的预测,温度值 $t$ 控制着知识转移的程度。
推导过程:
$K L(p \| q)=\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(\frac{p\left(x_{i}\right)}{q(x i)}\right)$
$\begin{array}{l} K L(p \| q)&=\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(p\left(x_{i}\right)\right)-\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(q\left(x_{i}\right)\right)\\&=H(p(x)) -\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(q\left(x_{i}\right)\right)\end{array}$
注意:$P$ 代表着真实分布, $Q$ 代表着模型分布;
注意:学生模型训练时,教师模型的参数是固定的,因此 $H(p(x))$ 为常数,可以去掉;
笔记:
$\operatorname{softmax}(x, T)_{l}=\frac{e^{x_{l} / T}}{\sum_{j} e^{v_{j} / T}}$
在计算 $\text{softmax}$ 的时候,$T$ 可以调节不同值的 “权重” :
-
- 当 $T<=1$ 时,标签中最大值的权重会较大,让标签分布更 “尖锐”;
- 当 $T>1$ 时,标签中最大值的权重会变小,除最大值以外的其它值权重会变大,让标签分布更“平滑”;
因此:
-
- 在 KD 中,需要软标签中除最大值以外其它值的信息,所以 $T>1$;
- 在 CL 中,难负例的贡献要高于简单负例更多,需要 $T<1$;
3 方法
3.1 模型框架
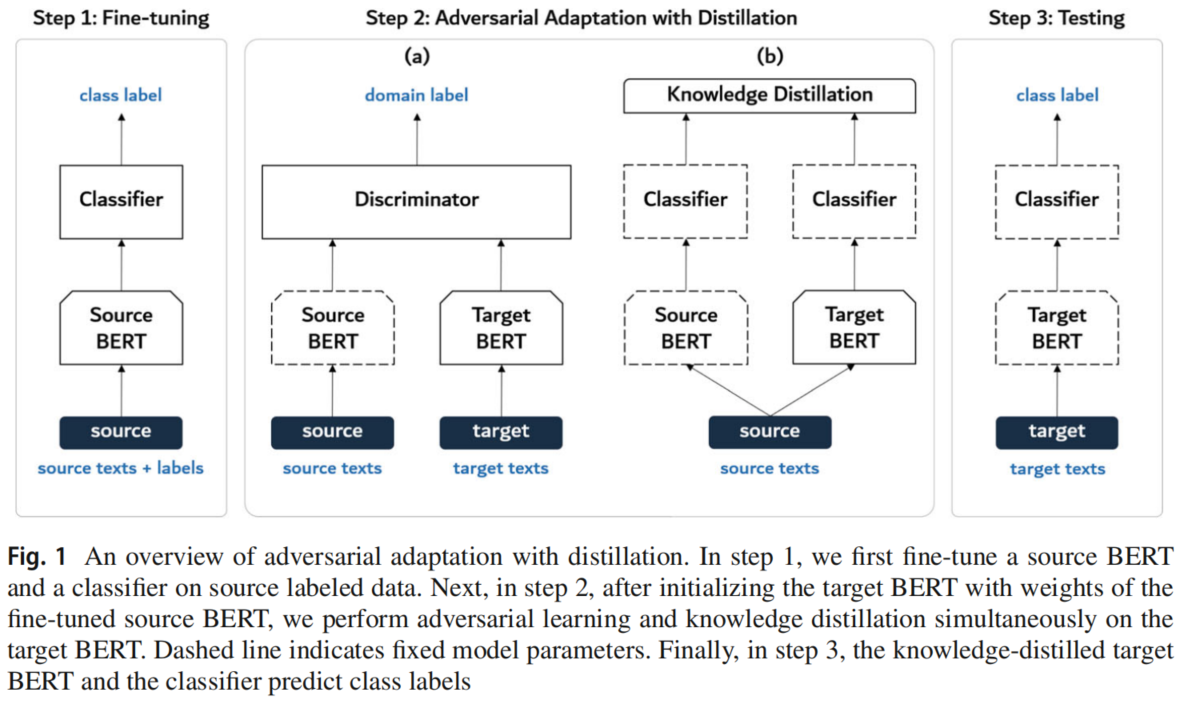
3.2 Adversarial adaptation with distillation
Step 1: fine-tune the source encoder and the classifier
使用源域数据进行标准的监督训练,训练 $E_s$ 和 $C$:
$\underset{E_{S}, C}{\text{min}} \; \mathcal{L}_{S}\left(\mathbf{X}_{S}, \mathbf{y}_{S}\right)=\mathbb{E}_{\left(\boldsymbol{x}_{s}, y_{s}\right) \sim\left(\mathbb{X}_{S}, \mathbb{Y}_{S}\right)}-\sum_{k=1}^{K} \mathbb{1}_{\left[k=y_{s}\right]} \log C\left(E_{S}\left(\boldsymbol{x}_{S}\right)\right)$
Step 2: adapt the target encoder via adversarial adaptation with distillation
固定 $E_s$ 的参数,并使用 $E_s$ 初始化 $E_t$ 的参数,接着进行对抗性训练:
$\begin{array}{l}\underset{D}{\text{min}} \; \mathcal{L}_{\text {dis }}\left(\mathbf{X}_{S}, \mathbf{X}_{T}\right)=\mathbb{E}_{\boldsymbol{x}_{s} \sim \mathbb{X}_{S}}-\log D\left(E_{s}\left(\boldsymbol{x}_{s}\right)\right)+\mathbb{E}_{\boldsymbol{x}_{t} \sim \mathbb{X}_{T}}-\log \left(1-D\left(E_{t}\left(\boldsymbol{x}_{t}\right)\right)\right)\\\underset{E_{t}}{\text{min}} \; \mathcal{L}_{g e n} \left(\mathbf{X}_{T}\right)=\mathbb{E}_{\boldsymbol{x}_{t} \sim \mathbb{X}_{T}}-\log D\left(E_{t}\left(\boldsymbol{x}_{t}\right)\right)\end{array}$
由于无法使用类标签,容易造成灾难性遗忘问题,从而导致分类性能下降。对于一个使用较大值 $t$ 的 KD 模型,不仅可以使得对抗性训练稳定,还可以良好的保存类信息。因此,引入了知识蒸馏损失:
$\mathcal{L}_{K D}\left(\mathbf{X}_{S}\right)=t^{2} \times \mathbb{E}_{\boldsymbol{x}_{s} \sim \mathbb{X}_{S}} \sum_{k=1}^{K}-\operatorname{softmax}\left(p_{k}^{S} / t\right) \times \log \left(\operatorname{softmax}\left(p_{k}^{T} / t\right)\right)$
因此,目标编码器 $E_{t}$ 的最终目标函数为:
$\underset{E_{t}}{\text{min}} \;\mathcal{L}_{T}\left(\mathbf{X}_{S}, \mathbf{X}_{T}\right)=\mathcal{L}_{\text {gen }}\left(\mathbf{X}_{T}\right)+\mathcal{L}_{K D}\left(\mathbf{X}_{S}\right)$
Step 3: test the target encoder on the target data
使用训练好的目标编码器 $E_{t}$ 和分类器 $C$ 对用于测试的目标数据情绪极性标签预测如下:
$\hat{y}_{t}=\arg \max C\left(E_{t}\left(\boldsymbol{x}_{t}\right)\right)$
4 实验
跨域情感分析
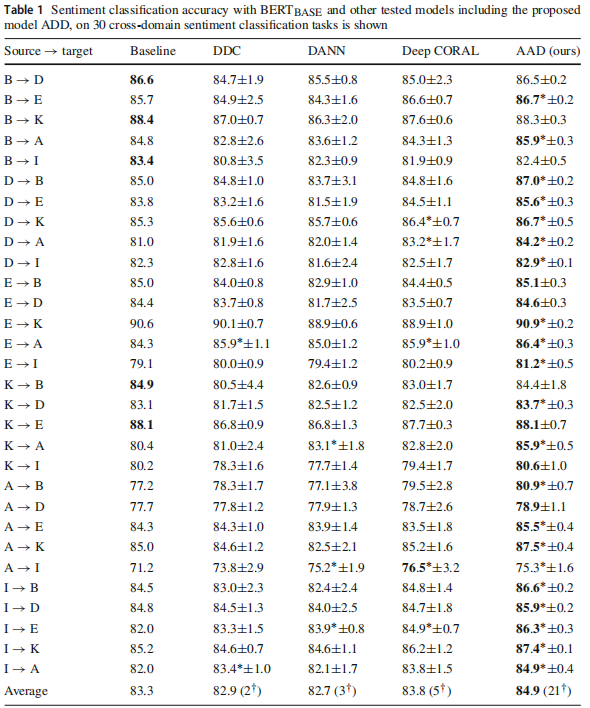
因上求缘,果上努力~~~~ 作者:别关注我了,私信我吧,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/17610000.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号