论文解读(CAT)《Cluster Alignment with a Teacher for Unsupervised Domain Adaptation》
Note:[ wechat:Y466551 | 付费咨询,非诚勿扰 ]
论文信息
论文标题:Cluster Alignment with a Teacher for Unsupervised Domain Adaptation
论文作者:Zhijie Deng, Yucen Luo, Jun Zhu
论文来源:2020 ICCV
论文地址:download
论文代码:download
视屏讲解:click
1 介绍
出发点:之前方法通常学习一个域不变的表示空间来匹配源域和目标域的边缘分布,而忽略它们的精细结构。在本文中,提出与教师聚类对齐的无监督域适应,可以有效地纳入两个域的鉴别聚类结构,以更好的适应;
贡献:
-
- 考虑并利用了深度UDA中分布的判别类条件结构,实现了类条件对齐;
- CAT 方法适用于现有的依赖于边际分布对准的UDA方法;
- CAT对超参数不敏感,且是 SOTA;
2 方法
2.1 模型框架
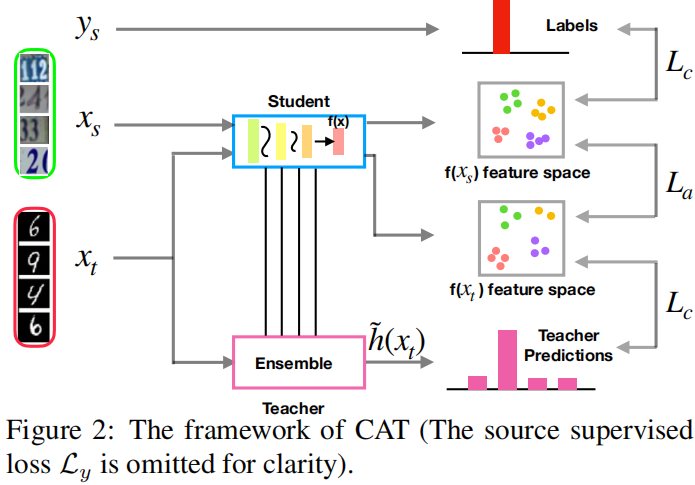
Note:教师模型 Π-model ,即同一个样本经过不同的 dropout 函数;
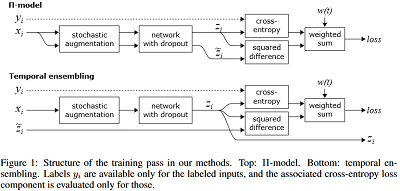
2.2 通过教师模型聚类对齐
目标:实现 鉴别性学习 和 类条件对齐学习?
$\underset{\theta}{\text{min}} \;\; \mathcal{L}_{y}+\alpha\left(\mathcal{L}_{c}+\mathcal{L}_{a}\right) $
2.2.1 鉴别性聚类通过教师模型
目标函数:
$\mathcal{L}_{c}\left(\mathcal{X}_{s}, \mathcal{X}_{t}\right)=\mathcal{L}_{c}\left(\mathcal{X}_{s}\right)+\mathcal{L}_{c}\left(\mathcal{X}_{t}\right)$
$\begin{aligned}\mathcal{L}_{c}(\mathcal{X})= \frac{1}{|\mathcal{X}|^{2}} \sum_{i=1}^{|\mathcal{X}|} \sum_{j=1}^{|\mathcal{X}|}\left[\delta_{i j} d\left(f\left(x^{i}\right), f\left(x^{j}\right)\right)+\right.\left.\left(1-\delta_{i j}\right) \max \left(0, m-d\left(f\left(x^{i}\right), f\left(x^{j}\right)\right)\right)\right]\end{aligned}$
其中 ,$\delta_{i j}$ 代表样本 $x_i$ 和 样本 $x_j$ 是不是同一类;
注意:$\mathcal{X}$ 指的是源域或者目标域,$\mathcal{L}_{c}$ 是 域内 的损失;
Note:目标域样本的标签(伪)由 教师分类器给出;
Note:可能会怀疑,教师分类器的错误预测是否会破坏训练的动态。然而,先前关于半监督学习[17,43]的研究已经验证了这种训练总是能导致良好的收敛性,并证明了对不正确标签的鲁棒性。
2.2.2 基于类条件特征对齐
类条件特征对齐(域间):
$ \underset{\theta}{\text{min}} \; \mathcal{D}\left(\mathcal{F}_{s, k} \| \mathcal{F}_{t, k}\right)$
其中,$\mathcal{F}_{s, k}\left(\mathcal{F}_{t, k}\right) $ 表示由属于源域(目标域)的类 $k$ 的所有特征组成的集合。
$\mathcal{L}_{a}\left(\mathcal{X}_{s}, \mathcal{Y}_{s}, \mathcal{X}_{t}\right)=\frac{1}{K} \sum_{k=1}^{K}\left\|\lambda_{s, k}-\lambda_{t, k}\right\|_{2}^{2}$
$\lambda_{t, k}=\frac{1}{\left|\mathcal{X}_{t, k}\;\right|} \sum_{x_{t}^{i}\; \in\; \mathcal{X}_{t, k\;}}\; f\left(x_{t}^{i}\right)$
2.3 通过边际分布对齐实现性能提升
事实:开始训练时,分类结果更多聚集在分类边界附近,而不是类别中心;
策略:同时将几何上更接近源域的自信实例与源数据对齐;
对抗性训练目标函数(基于置信度):
$\begin{array}{c} \underset{\theta}{\text{min}} \; \underset{\phi}{\text{max}}\; \mathcal{L}_{d}\left(\mathcal{X}_{s}, \mathcal{X}_{t}\right)=\frac{1}{N} \sum_{i=1}^{N}\left[\log c\left(f\left(x_{s}^{i} ; \theta\right) ; \phi\right)\right]+ \frac{1}{\tilde{M}} \sum_{i=1}^{\tilde{M}}\left[\log \left(1-c\left(f\left(x_{t}^{i} ; \theta\right) ; \phi\right)\right) \gamma_{i}\right]\end{array}$
3 实验
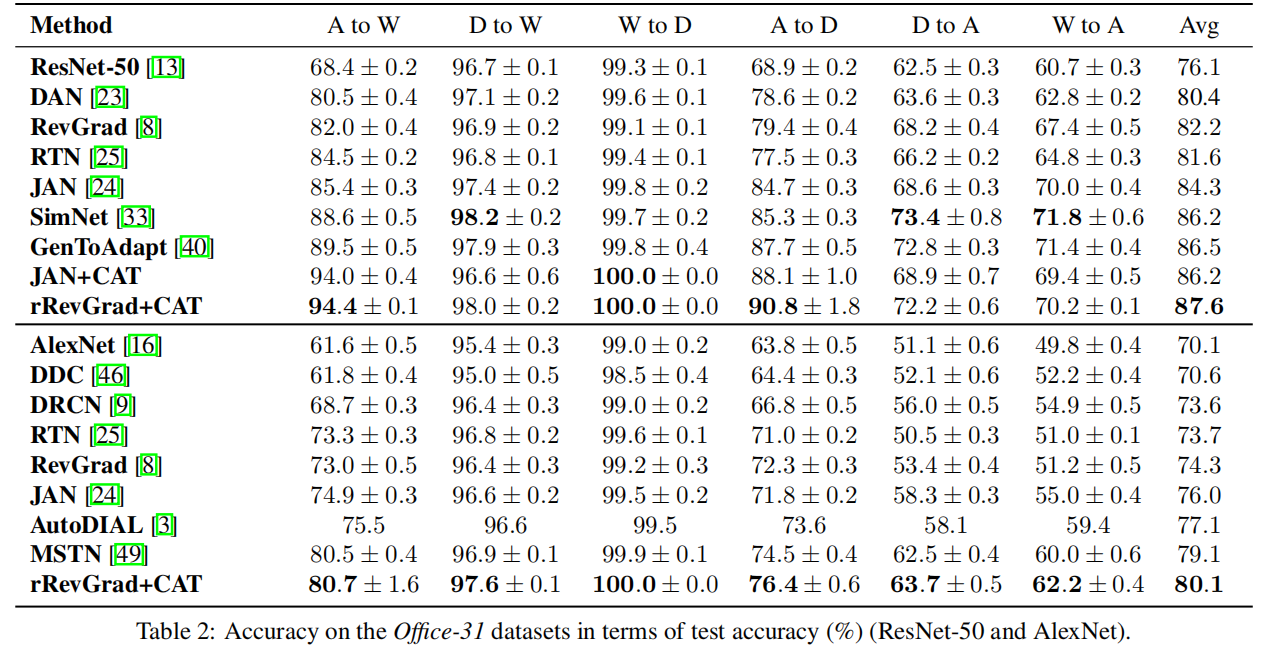
因上求缘,果上努力~~~~ 作者:别关注我了,私信我吧,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/17596624.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号