迁移学习（TSRP）《Improving Pseudo Labels With Intra-Class Similarity for Unsupervised Domain Adaptation》

论文信息

论文标题：Improving Pseudo Labels With Intra-Class Similarity for Unsupervised Domain Adaptation
论文作者：Jie Wang, Xiaoli Zhang
论文来源：July 2022——ArXiv 
论文地址：download 
论文代码：download
视屏讲解：click

1 介绍

　　问题：

• • 首先，伪标签主要是通过源域和目标域之间的良好对齐获得的，而伪标签的准确性对性能的影响没有深入研究。通常在源域上训练分类器生成伪标签时，在每次优化迭代中都可能出现一些错误的伪标签，如 Figure1 所示。由于错误的累积，不正确的伪标签会极大地影响最终的性能；
  • 其次，大多数方法主要集中在挖掘源域以提高目标域伪标签的准确性，目标域样本之间的内在关系似乎还没有被探索；

　　　　

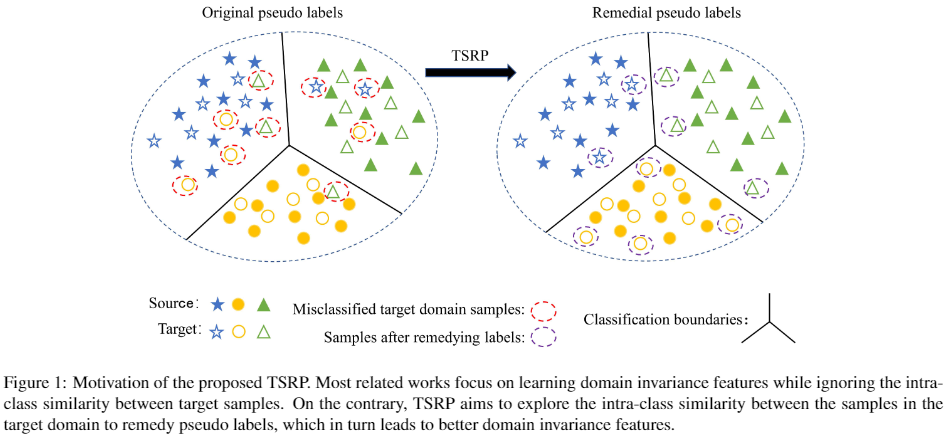
　　为了解决上述两个问题，在本文中，提出挖掘目标域类内相似性来修复目标域中的伪标签（TSRP），以提高伪标签的准确性。 TSRP 的核心思想是使用目标相似性通过生成树 [22] 来选择具有高置信度的伪标签（UTSP）。 然后，使用选择的高置信度伪标记样本和源数据来训练强分类器。 强分类器用于纠正部分错误标记的具有低置信度伪标签的目标样本。 我们称之为伪标签的补救过程。 通常，我们的方法可以集成到任何通过使用在源域上训练的分类器生成目标域的伪标签的方法。

2 相关工作

　　在 [37] 中，Saito 等人。 使用三个非对称分类器来提高伪标签的准确性，其中两个分类器用于选择置信伪标签，第三个旨在学习目标域的判别数据表示。 [18]通过结构化预测探索目标域的结构信息，并结合最近的类原型和结构化预测来提升伪标签的准确性。 [38]将目标域中同一簇的样本视为一个整体而不是个体。 它通过类质心匹配为目标集群分配伪标签。 [39]提出了一种从易到难的策略，将目标样本分为三类，即简单样本、困难样本和不正确的简单样本。 它倾向于为简单的样本生成伪标签，并尽量避免困难的样本。 从易到难的策略可能偏向于简单的类。 为了解决这个问题，[40] 中提出了一种置信度感知的伪标签选择策略。 它根据伪标签的概率独立地从每个类中选择样本。 在 [39, 40] 中，他们使用目标样本到源样本中心的距离作为选择标准来选择高度置信度的伪标签。 在 [18, 38] 中，他们迭代地生成可信的伪标签。 但是，他们没有考虑如何纠正错误生成的伪标签。 与上述方法不同，在本文中，我们建议通过探索目标域中的类内相似性来纠正错误生成的伪标签。

3 方法

　　整体框架：

　　

　　整体算法：

　　

　　UTSP 如下：

　　

　　UTSP 图解如下：

　　

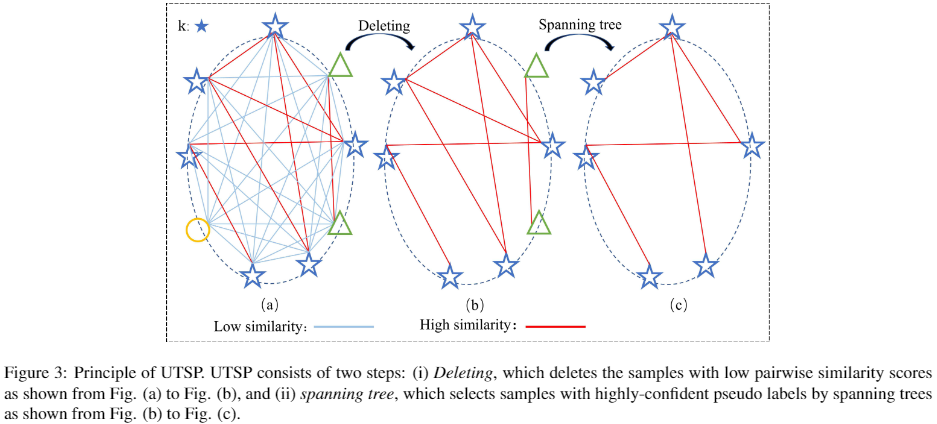
　　公式：

　　　　$\hat{\mathbf{y}}_{l, \text { remedy }}^{T}=f_{\text {strong }}\left(\mathbf{Z}_{l}^{T}\right)   \quad\quad\quad(1)$

　　　　$S_{i, j}^{k}=\left\{\begin{array}{ll}0, & i=j \\\frac{\left\langle\mathbf{z}_{i}^{T k}, \mathbf{z}_{j}^{T k}\right\rangle}{\left\|\mathbf{z}_{i}^{T i}\right\|\left\|\mathbf{z}_{j}^{T k k}\right\|}, & \text { otherwise }\end{array}, \forall k=1,2, \ldots, C_{y}\right. \quad\quad\quad(2)$

　　　　$S_{\text {rank }}^{k}=\left\{S_{\operatorname{rank}(1)}^{k}, S_{\operatorname{rank}(2)}^{k}, \ldots, S_{\operatorname{rank}\left(n_{p}\right)}^{k}\right\} \quad\quad\quad(3)$

　　　　$\delta=S_{\left.\operatorname{rank}\left(\mid \rho n_{p}\right\rfloor\right)}^{k}  \quad\quad\quad(4)$

　　　　$M_{i j}^{k}=\left\{\begin{array}{ll}1, & S_{i, j}^{k} \geq \delta \\0, & \text { otherwise }\end{array}\right.  \quad\quad\quad(5)$

　　　　$D_{i i}^{k}=\sum\limits _{j} M_{i j}^{k}  \quad\quad\quad(6)$

　　　　$m=\arg \underset{i}{\text{max}} D_{i i}^{k}   \quad\quad\quad(7)$

　　Note：为防止类不平衡问题，将某类 $i$ 样本数少于 $3$  的全部视为高置信度样本；

4 实验

Performance 

　　

消融实验

　　

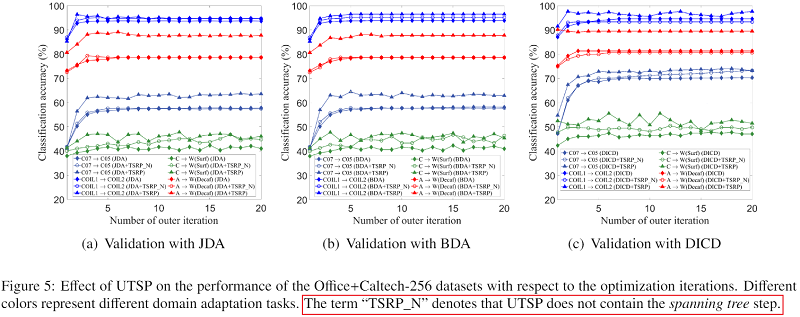
5 总结

 

 

论文：

标签生成策略：硬标签[19、35、17] 和 软标签[36]

伪标签产生负面影响：[18]