论文解读《Modeling Discriminative Representations for Out-of-Domain Detection with Supervised Contrastive Learning》

论文信息

论文标题：Modeling Discriminative Representations for Out-of-Domain Detection with Supervised Contrastive Learning
论文作者：Zhiyuan Zeng, Keqing He, Yuanmeng Yan, Zijun Liu, Yanan Wu, Hong Xu, Huixing Jiang, Weiran Xu
论文来源：ACL 2021
论文地址：download 
论文代码：download
引用次数：

1 前言

　　贡献：

• • 提出了一个有监督的对比学习目标，通过把属于同一类别的域内意图拉到一起，使类内方差最小化，通过把不同类别的样本推开，使类间方差最大化；
  • 采用了一种对抗性的增强机制，以获得潜伏空间中样本的假性不同观点；

2 方法

　　整体框架：

　　

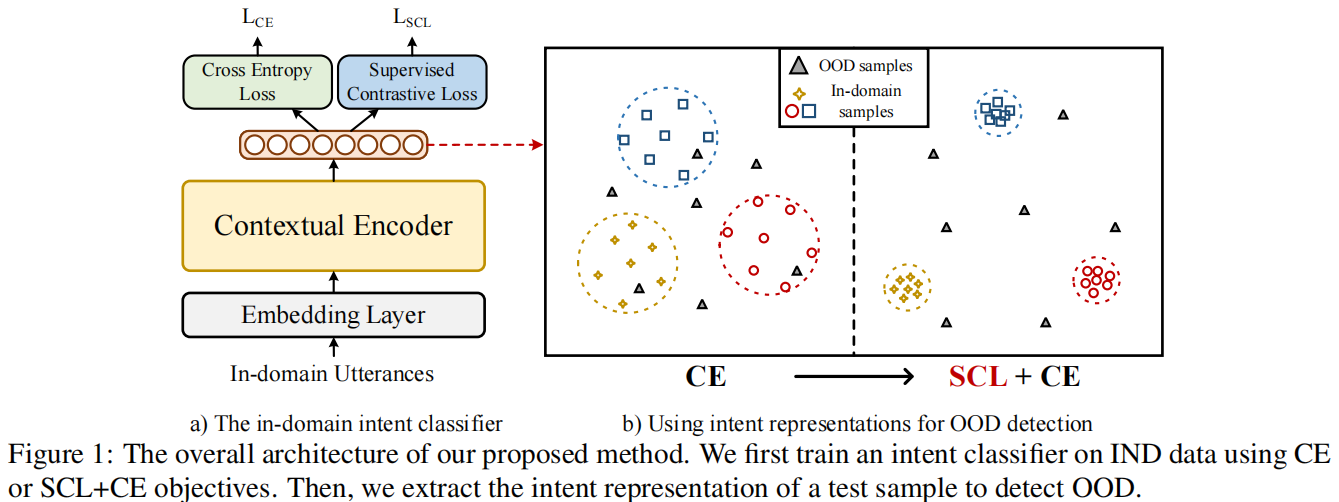
　　损失函数：

　　　　交叉熵损失函数：

　　　　　　$\mathcal{L}_{C E}=\frac{1}{N} \sum_{i}-\log \frac{e^{W_{y_{i}}^{T} s_{i} / \tau}}{\sum_{j} e^{W_{j}^{T} s_{i} / \tau}}$

　　　　最大边际余弦损失 (LMCL)：　　　　

　　　　　　$\mathcal{L}_{L M C L}=\frac{1}{N} \sum_{i}-\log \frac{e^{W_{y_{i}}^{T} s_{i} / \tau}}{e^{W_{y_{i}}^{T} s_{i} / \tau}+\sum_{j \neq y_{i}} e^{\left(W_{j}^{T} s_{i}+m\right) / \tau}}$

　　　　对比损失（SCL）：

　　　　　　$\begin{aligned}\mathcal{L}_{S C L}= & \sum_{i=1}^{N}-\frac{1}{N_{y_{i}}-1} \sum_{j=1}^{N} \mathbf{1}_{i \neq j} \mathbf{1}_{y_{i}=y_{j}} \log \frac{\exp \left(s_{i} \cdot s_{j} / \tau\right)}{\sum_{k=1}^{N} \mathbf{1}_{i \neq k} \exp \left(s_{i} \cdot s_{k} / \tau\right)}\end{aligned}$

　　数据增强：

　　　　对抗攻击：

　　　　　　$\mathcal{L}_{C E}: \boldsymbol{\delta}=\underset{\left\|\boldsymbol{\delta}^{\prime}\right\| \leq \epsilon}{\arg \max } \mathcal{L}_{C E}\left(\boldsymbol{\theta}, \boldsymbol{x}+\boldsymbol{\delta}^{\prime}\right)$

　　　　　　$\boldsymbol{\delta}=\epsilon \frac{g}{\|g\|} ; \text { where } g=\nabla_{\boldsymbol{x}} \mathcal{L}_{C E}(f(\boldsymbol{x} ; \boldsymbol{\theta}), y)$

　　　　　　$\boldsymbol{x}_{a d v}=\boldsymbol{x}+\boldsymbol{\delta}$

 

3 代码

交叉熵损失：

 

probs = torch.softmax(logits, dim=1)
ce_loss = torch.sum(torch.mul(-torch.log(probs), label))

最大边际余弦损失：

def lmcl_loss(probs, label, margin=0.35, scale=30):
    probs = label * (probs - margin) + (1 - label) * probs
    probs = torch.softmax(probs, dim=1)
    return probs

对比损失：

def pair_cosine_similarity(x, x_adv, eps=1e-8):
    n = x.norm(p=2, dim=1, keepdim=True)
    n_adv = x_adv.norm(p=2, dim=1, keepdim=True)
    return (x @ x.t()) / (n * n.t()).clamp(min=eps), (x_adv @ x_adv.t()) / (n_adv * n_adv.t()).clamp(min=eps), (x @ x_adv.t()) / (n * n_adv.t()).clamp(min=eps)


def nt_xent(x, x_adv, mask, cuda=True, t=0.1):
    x, x_adv, x_c = pair_cosine_similarity(x, x_adv)
    x = torch.exp(x / t)
    x_adv = torch.exp(x_adv / t)
    x_c = torch.exp(x_c / t)
    mask_count = mask.sum(1)
    mask_reverse = (~(mask.bool())).long()
    if cuda:
        dis = (x * (mask - torch.eye(x.size(0)).long().cuda()) + x_c * mask) / (x.sum(1) + x_c.sum(1) - torch.exp(torch.tensor(1 / t))) + mask_reverse
        dis_adv = (x_adv * (mask - torch.eye(x.size(0)).long().cuda()) + x_c.T * mask) / (x_adv.sum(1) + x_c.sum(0) - torch.exp(torch.tensor(1 / t))) + mask_reverse
    else:
        dis = (x * (mask - torch.eye(x.size(0)).long()) + x_c * mask) / (x.sum(1) + x_c.sum(1) - torch.exp(torch.tensor(1 / t))) + mask_reverse
        dis_adv = (x_adv * (mask - torch.eye(x.size(0)).long()) + x_c.T * mask) / (x_adv.sum(1) + x_c.sum(0) - torch.exp(torch.tensor(1 / t))) + mask_reverse
    loss = (torch.log(dis).sum(1) + torch.log(dis_adv).sum(1)) / mask_count
    return -loss.mean()