迁移学习(HDAN)《Heuristic Domain Adaptation》(已复现迁移)
论文信息
论文标题:Heuristic Domain Adaptation
论文作者:Shuhao Cui, Xuan Jin, Shuhui Wang, Yuan He, Qingming Huang
论文来源:NeurIPS 2020
论文地址:download
论文代码:download
1 介绍
-
- domain-invariant representations $G(x)$ :不随着域的变化而改变,包含的是类信息;
-
- domain-specifific representations $H(x)$:与类信息无关的环境信息;
问题描述:域不变特征从整体特征中很难分离出来。
解决方法:启发式搜索
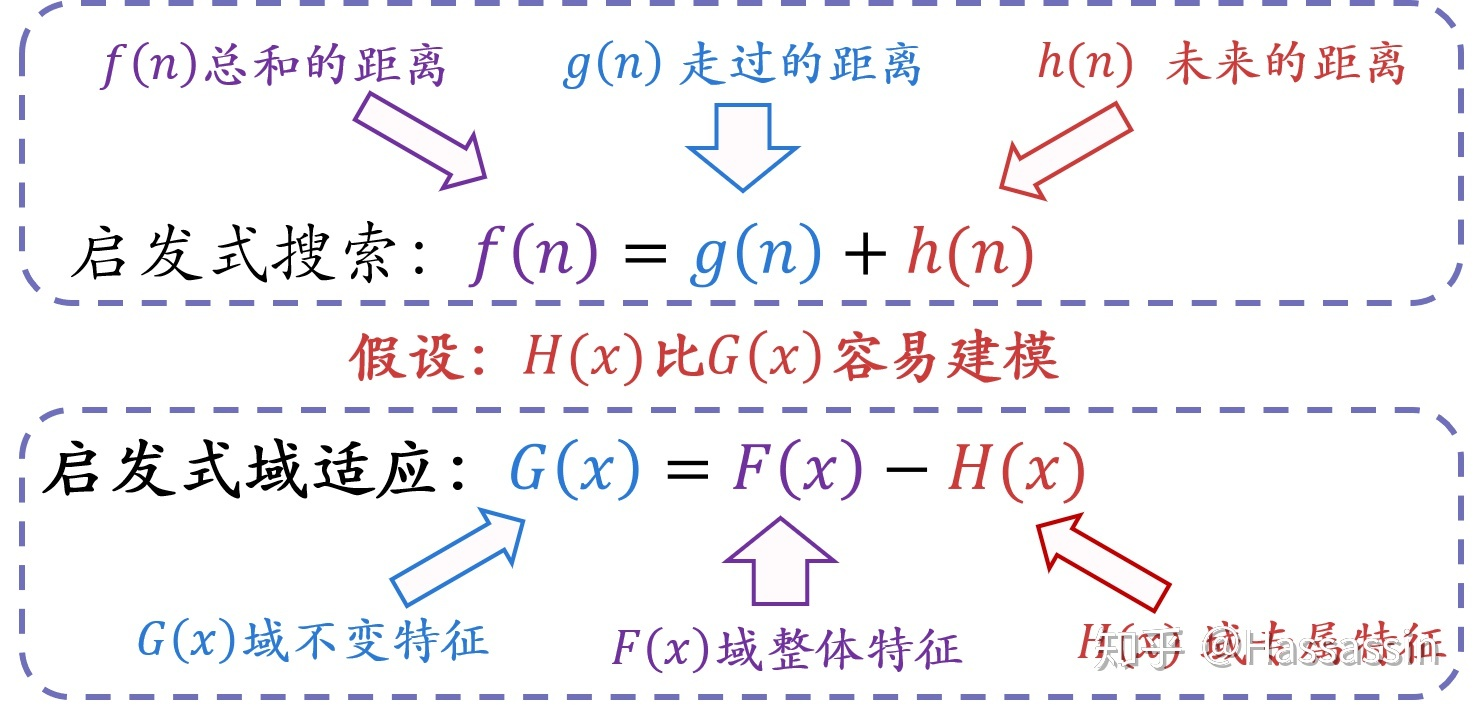
2 方法
整体框架:
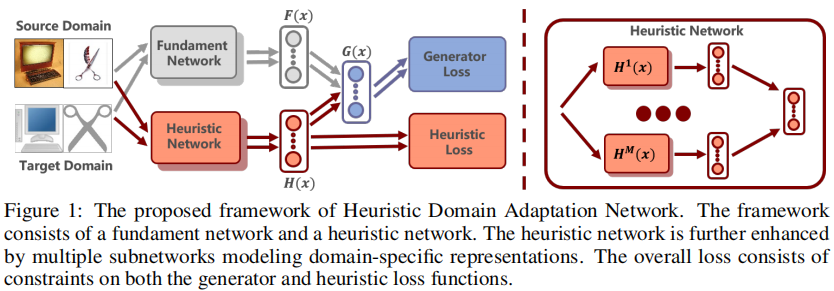
$G(x)$ 与 $H(x)$ 应该是有区分的,使用余弦相似度建模两者之间的相似性:
$\cos (\theta)=\frac{G(x) \cdot H(x)}{|G(x)||H(x)|}$
理论上:$G(x)$ 应该在不同的域之间保持相同,而 $H(x)$ 在不同的域之间是不同的。
期望两者之间的相似性为 $0$,所以初始化为:
$H_{i n i t}(x)=-G_{i n i t}(x)$
优化目标:
$\mathcal{L}_{F}=\mathcal{L}_{G}+\mathcal{L}_{H}=\mathcal{L}_{C l s}+\mathcal{L}_{\text {Trans }}+\mathcal{L}_{H} .$
其中:
-
- heuristic loss $\mathcal{L}_{H}$
- generator loss $\mathcal{L}_{G}$ 包括 classification loss $\mathcal{L}_{C l s}$ 和 transfer loss $\mathcal{L}_{\text {Trans }}$
generator loss $\mathcal{L}_{G}$ 具体如下:
$\begin{array}{l}\left.\mathcal{L}_{C l s}=\mathbb{E}_{\left(x_{i}^{s}, y_{i}^{s}\right) \sim \mathcal{D}_{s}} L_{c e}\left(G\left(x_{i}^{s}\right)\right), y_{i}^{s}\right) \\\mathcal{L}_{\text {Trans }}=-\mathbb{E}_{x_{i}^{s} \sim \mathcal{D}_{s}} \log \left[D\left(G\left(x_{i}^{s}\right)\right)\right]-\mathbb{E}_{x_{j}^{t} \sim \mathcal{D}_{T}} \log \left[1-D\left(G\left(x_{j}^{t}\right)\right)\right]\end{array}$
heuristic loss $\mathcal{L}_{H}$ 具体如下:
$\mathcal{L}_{H}=\mathbb{E}_{x_{i} \sim\left(\mathcal{D}_{S}, \mathcal{D}_{T}\right)}\left|H\left(x_{i}\right)\right|_{1}=\mathbb{E}_{x_{i} \sim\left(\mathcal{D}_{S}, \mathcal{D}_{T}\right)}\left|\Sigma_{k=1}^{M} H^{k}\left(x_{i}\right)\right|_{1}$
3 实验
3.1 无监督域适应 [Unsupervised Domain Adaptation ]
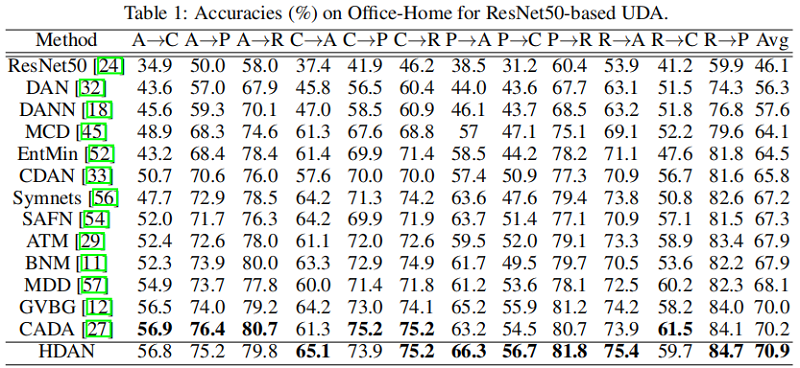
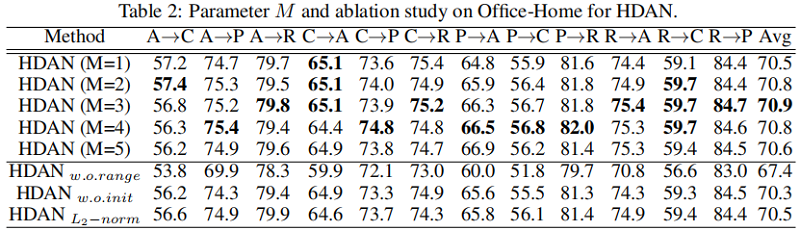
通过构建实验来判断 $G(x)$ 与 $H(x)$ 是源域还是目标域,$H(x)$ 可区分性更强,也说明 $H(x)$ 比 $G(x)$ 容易建模。
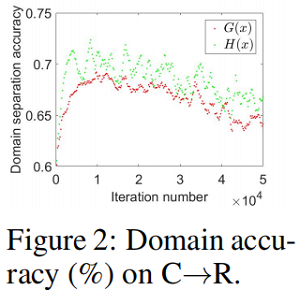
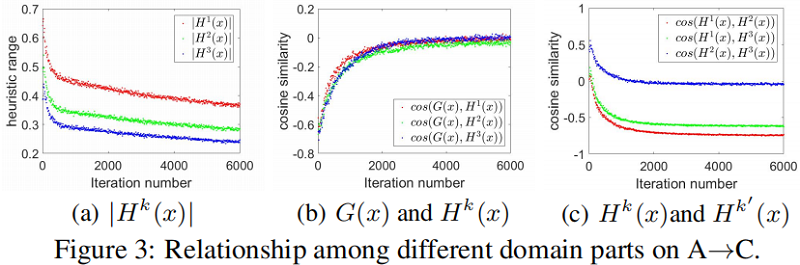
$G(x)$ 与 $H(x)$ 的相似度分析结果展示出两者的相似性逐渐降低,然而我们认为 $G(x)$ 更多建模领域无关特征,相应的 $H(x)$ 建模领域特性。
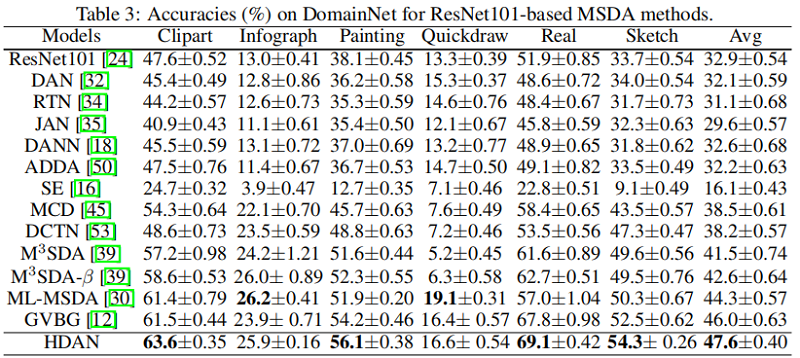
3.2 多源域适应
3.3 半监督的领域自适应

因上求缘,果上努力~~~~ 作者:图神经网络,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/17092909.html


