论文信息
论文标题:Domain-Adversarial Training of Neural Networks 论文作者:Yaroslav Ganin, Evgeniya Ustinova, Hana Ajakan, Pascal Germain 论文来源:JMLR 2016 论文地址:download 论文代码:download 引用次数:5292
1 域适应 We consider classification tasks where X X Y = { 0 , 1 , … , L − 1 } Y = { 0 , 1 , … , L − 1 } L L X × Y X × Y D S D S D T D T S S D S D S T T D X T D T X D X T D T X D T D T X X
S = { ( x i , y i ) } n i = 1 ∼ ( D S ) n S = { ( x i , y i ) } i = 1 n ∼ ( D S ) n
T = { x i } N i = n + 1 ∼ ( D X T ) n ′ T = { x i } i = n + 1 N ∼ ( D T X ) n ′
with N = n + n ′ N = n + n ′ η : X → Y η : X → Y
R D T ( η ) = Pr ( x , y ) ∼ D T ( η ( x ) ≠ y ) , R D T ( η ) = Pr ( x , y ) ∼ D T ( η ( x ) ≠ y ) ,
while having no information about the labels of D T D T
2 Domain Divergence 假设 :如果数据来自源域,域标签为 1 1 0 0
Definition 1 . Given two domain distributions D X S D S X D X T D T X X X H H H -divergence H -divergence D X S D S X D X T D T X
d H ( D X S , D X T ) = 2 sup η ∈ H ∣ ∣ Pr x ∼ D X S [ η ( x ) = 1 ] − Pr x ∼ D X T [ η ( x ) = 1 ] ∣ ∣ d H ( D S X , D T X ) = 2 sup η ∈ H | Pr x ∼ D S X [ η ( x ) = 1 ] − Pr x ∼ D T X [ η ( x ) = 1 ] |
H -divergence H -divergence H H h h Pr x ∼ D [ h ( x ) = 1 ] Pr x ∼ D [ h ( x ) = 1 ] Pr x ∼ D ′ [ h ( x ) = 1 ] Pr x ∼ D ′ [ h ( x ) = 1 ]
可通过计算样本 S ∼ ( D X S ) n S ∼ ( D S X ) n T ∼ ( D X T ) n ′ T ∼ ( D T X ) n ′ H-divergence H-divergence
^ d H ( S , T ) = 2 ( 1 − min η ∈ H [ 1 n n ∑ i = 1 I [ η ( x i ) = 0 ] + 1 n ′ N ∑ i = n + 1 I [ η ( x i ) = 1 ] ] ) ( 1 ) d ^ H ( S , T ) = 2 ( 1 − min η ∈ H [ 1 n ∑ i = 1 n I [ η ( x i ) = 0 ] + 1 n ′ ∑ i = n + 1 N I [ η ( x i ) = 1 ] ] ) ( 1 )
其中,I [ a ] I [ a ] a a I [ a ] = 1 I [ a ] = 1 I [ a ] = 0 I [ a ] = 0
3 Proxy Distance 由于经验 H -divergence H -divergence
构造新的数据集 U U
U = { ( x i , 0 ) } n i = 1 ∪ { ( x i , 1 ) } N i = n + 1 ( 2 ) U = { ( x i , 0 ) } i = 1 n ∪ { ( x i , 1 ) } i = n + 1 N ( 2 )
使用 H -divergence H -divergence Proxy A-distance(PAD) Proxy A-distance(PAD)
^ d A = 2 ( 1 − 2 ϵ ) ( 3 ) d ^ A = 2 ( 1 − 2 ϵ ) ( 3 )
其中,ϵ ϵ
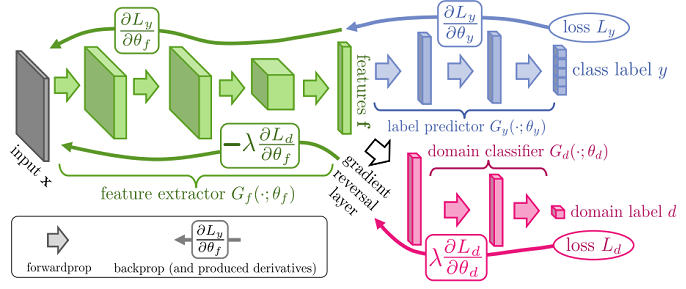
4 Method 假设输入空间由 m m X = R m X = R m G f : X → R D G f : X → R D ( W , b ) ∈ R D × m × R D ( W , b ) ∈ R D × m × R D
G f ( x ; W , b ) = sigm ( W x + b ) with sigm ( a ) = [ 1 1 + exp ( − a i ) ] | a | i = 1 ( 4 ) G f ( x ; W , b ) = sigm ( W x + b ) with sigm ( a ) = [ 1 1 + exp ( − a i ) ] i = 1 | a | ( 4 )
预测层 G y : R D → [ 0 , 1 ] L G y : R D → [ 0 , 1 ] L ( V , c ) ∈ R L × D × R L ( V , c ) ∈ R L × D × R L
G y ( G f ( x ) ; V , c ) = softmax ( V G f ( x ) + c ) with softmax ( a ) = [ exp ( a i ) ∑ | a | j = 1 exp ( a j ) ] | a | i = 1 G y ( G f ( x ) ; V , c ) = softmax ( V G f ( x ) + c ) with softmax ( a ) = [ exp ( a i ) ∑ j = 1 | a | exp ( a j ) ] i = 1 | a |
其中 L = | Y | L = | Y |
给定一个源样本 ( x i , y i ) ( x i , y i )
L y ( G y ( G f ( x i ) ) , y i ) = log 1 G y ( G f ( x ) ) y i L y ( G y ( G f ( x i ) ) , y i ) = log 1 G y ( G f ( x ) ) y i
对神经网络的训练会导致源域上的以下优化问题:
min W , b , V , c [ 1 n ∑ n i = 1 L i y ( W , b , V , c ) + λ ⋅ R ( W , b ) ] ( 5 ) min W , b , V , c [ 1 n ∑ i = 1 n L y i ( W , b , V , c ) + λ ⋅ R ( W , b ) ] ( 5 )
其中,L i y ( W , b , V , c ) = L y ( G y ( G f ( x i ; W , b ) ; V , c ) , y i ) L y i ( W , b , V , c ) = L y ( G y ( G f ( x i ; W , b ) ; V , c ) , y i ) R ( W , b ) R ( W , b )
域正则化器引出想法:借用 Definition 1 Definition 1 H H
源样本、目标样本分别表示为
S ( G f ) = { G f ( x ) ∣ x ∈ S } S ( G f ) = { G f ( x ) ∣ x ∈ S }
T ( G f ) = { G f ( x ) ∣ x ∈ T } T ( G f ) = { G f ( x ) ∣ x ∈ T }
在 Eq.1 Eq.1 S ( G f ) S ( G f ) T ( G f ) T ( G f ) H -divergence H -divergence
^ d H ( S ( G f ) , T ( G f ) ) = 2 ( 1 − min η ∈ H [ 1 n n ∑ i = 1 I [ η ( G f ( x i ) ) = 0 ] + 1 n ′ N ∑ i = n + 1 I [ η ( G f ( x i ) ) = 1 ] ] ) ( 6 ) d ^ H ( S ( G f ) , T ( G f ) ) = 2 ( 1 − min η ∈ H [ 1 n ∑ i = 1 n I [ η ( G f ( x i ) ) = 0 ] + 1 n ′ ∑ i = n + 1 N I [ η ( G f ( x i ) ) = 1 ] ] ) ( 6 )
域分类器 G d : R D → [ 0 , 1 ] G d : R D → [ 0 , 1 ] ( u , z ) ∈ R D × R ( u , z ) ∈ R D × R D X S D S X D X T D T X
G d ( G f ( x ) ; u , z ) = sigm ( u ⊤ G f ( x ) + z ) ( 7 ) G d ( G f ( x ) ; u , z ) = sigm ( u ⊤ G f ( x ) + z ) ( 7 )
因此,域分类器的交叉熵损失如下:
L d ( G d ( G f ( x i ) ) , d i ) = d i log 1 G d ( G f ( x i ) ) + ( 1 − d i ) log 1 1 − G d ( G f ( x i ) ) L d ( G d ( G f ( x i ) ) , d i ) = d i log 1 G d ( G f ( x i ) ) + ( 1 − d i ) log 1 1 − G d ( G f ( x i ) )
其中,d i d i i i
Eq.5 Eq.5
R ( W , b ) = max u , z [ − 1 n n ∑ i = 1 L i d ( W , b , u , z ) − 1 n ′ N ∑ i = n + 1 L i d ( W , b , u , z ) ] ( 8 ) R ( W , b ) = max u , z [ − 1 n ∑ i = 1 n L d i ( W , b , u , z ) − 1 n ′ ∑ i = n + 1 N L d i ( W , b , u , z ) ] ( 8 )
其中,L i d ( W , b , u , z ) = L d ( G d ( G f ( x i ; W , b ) ; u , z ) , d i ) L d i ( W , b , u , z ) = L d ( G d ( G f ( x i ; W , b ) ; u , z ) , d i )
△ R ( W , b ) R ( W , b ) Eq.6 Eq.6 H -divergence H -divergence 2 ( 1 − R ( W , b ) ) 2 ( 1 − R ( W , b ) ) ^ d H ( S ( G f ) , T ( G f ) ) d ^ H ( S ( G f ) , T ( G f ) )
Eq.5 Eq.5
E ( W , V , b , c , u , z ) = 1 n n ∑ i = 1 L i y ( W , b , V , c ) − λ ( 1 n n ∑ i = 1 L i d ( W , b , u , z ) + 1 n ′ ∑ N i = n + 1 L i d ( W , b , u , z ) ) ( 9 ) E ( W , V , b , c , u , z ) = 1 n ∑ i = 1 n L y i ( W , b , V , c ) − λ ( 1 n ∑ i = 1 n L d i ( W , b , u , z ) + 1 n ′ ∑ i = n + 1 N L d i ( W , b , u , z ) ) ( 9 )
对应的参数优化 ^ W W ^ ^ V V ^ ^ b b ^ ^ c c ^ ^ u u ^ ^ z z ^
( ^ W , ^ V , ^ b , ^ c ) = arg min W , V , b , c E ( W , V , b , c , ^ u , ^ z ) ( ^ u , ^ z ) = arg max u , z E ( ^ W , ^ V , ^ b , ^ c , u , z ) ( W ^ , V ^ , b ^ , c ^ ) = arg min W , V , b , c E ( W , V , b , c , u ^ , z ^ ) ( u ^ , z ^ ) = arg max u , z E ( W ^ , V ^ , b ^ , c ^ , u , z )
Generalization to Arbitrary Architectures
分类损失和域分类损失:
L i y ( θ f , θ y ) = L y ( G y ( G f ( x i ; θ f ) ; θ y ) , y i ) L i d ( θ f , θ d ) = L d ( G d ( G f ( x i ; θ f ) ; θ d ) , d i ) L y i ( θ f , θ y ) = L y ( G y ( G f ( x i ; θ f ) ; θ y ) , y i ) L d i ( θ f , θ d ) = L d ( G d ( G f ( x i ; θ f ) ; θ d ) , d i )
优化目标:
E ( θ f , θ y , θ d ) = 1 n n ∑ i = 1 L i y ( θ f , θ y ) − λ ( 1 n n ∑ i = 1 L i d ( θ f , θ d ) + 1 n ′ N ∑ i = n + 1 L i d ( θ f , θ d ) ) ( 10 ) E ( θ f , θ y , θ d ) = 1 n ∑ i = 1 n L y i ( θ f , θ y ) − λ ( 1 n ∑ i = 1 n L d i ( θ f , θ d ) + 1 n ′ ∑ i = n + 1 N L d i ( θ f , θ d ) ) ( 10 )
对应的参数优化 ^ θ f θ ^ f ^ θ y θ ^ y ^ θ d θ ^ d
( ^ θ f , ^ θ y ) = argmin θ f , θ y E ( θ f , θ y , ^ θ d ) ( 11 ) ^ θ d = argmax θ d E ( ^ θ f , ^ θ y , θ d ) ( 12 ) ( θ ^ f , θ ^ y ) = argmin θ f , θ y E ( θ f , θ y , θ ^ d ) ( 11 ) θ ^ d = argmax θ d E ( θ ^ f , θ ^ y , θ d ) ( 12 )
如前所述,由 Eq.11-Eq.12 Eq.11-Eq.12
θ f ⟵ θ f − μ ( ∂ L i y ∂ θ f − λ ∂ L i d ∂ θ f ) ( 13 ) θ y ⟵ θ y − μ ∂ L i y ∂ θ y ( 14 ) θ d ⟵ θ d − μ λ ∂ L i d ∂ θ d ( 15 ) θ f ⟵ θ f − μ ( ∂ L y i ∂ θ f − λ ∂ L d i ∂ θ f ) ( 13 ) θ y ⟵ θ y − μ ∂ L y i ∂ θ y ( 14 ) θ d ⟵ θ d − μ λ ∂ L d i ∂ θ d ( 15 )
整体框架:
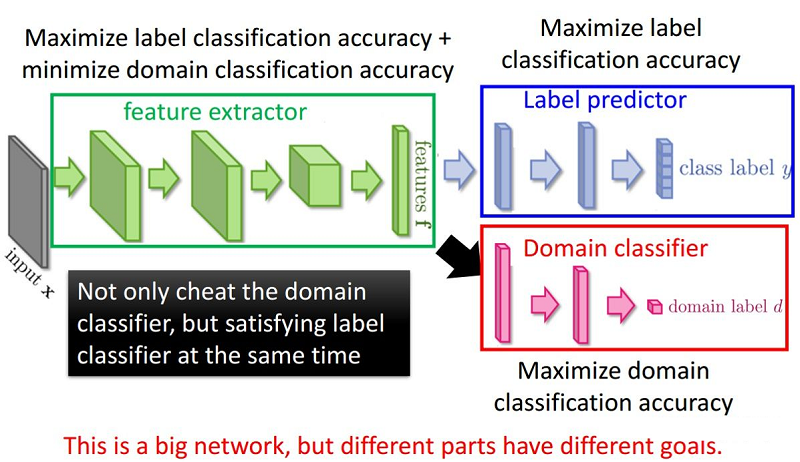
5 总结 问题:
for epoch in range(n_epoch):
len_dataloader = min(len(dataloader_source), len(dataloader_target))
data_source_iter = iter(dataloader_source)
data_target_iter = iter(dataloader_target)
i = 0
while i < len_dataloader:
p = float(i + epoch * len_dataloader) / n_epoch / len_dataloader
alpha = 2. / (1. + np.exp(-10 * p)) - 1
# training model using source data
data_source = data_source_iter.next()
s_img, s_label = data_source
class_output, domain_output = my_net(input_data=s_img, alpha=alpha)
err_s_label = loss_class(class_output, class_label)
err_s_domain = loss_domain(domain_output, domain_label)
# training model using target data
t_img, _ = data_target_iter.next()
domain_label = torch.ones(batch_size)
domain_label = domain_label.long()
_, domain_output = my_net(input_data=t_img, alpha=alpha)
err_t_domain = loss_domain(domain_output, domain_label)
err = err_t_domain + err_s_domain + err_s_label
err.backward()
optimizer.step()
i += 1
def forward(self, input_data, alpha):
feature = self.feature(input_data)
class_output = self.class_classifier(feature)
reverse_feature = ReverseLayerF.apply(feature, alpha)
domain_output = self.domain_classifier(reverse_feature)
return class_output, domain_output




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识?