论文解读（CAN）《Contrastive Adaptation Network for Unsupervised Domain Adaptation》

Note：[ wechat：Y466551 | 可加勿骚扰，付费咨询 ] 2024年4月6日19:08:16

论文信息

论文标题：Contrastive Adaptation Network for Unsupervised Domain Adaptation
论文作者：Guoliang Kang, Lu Jiang, Yi Yang, Alexander G Hauptmann
论文来源：CVPR 2019
论文地址：download 
论文代码：download

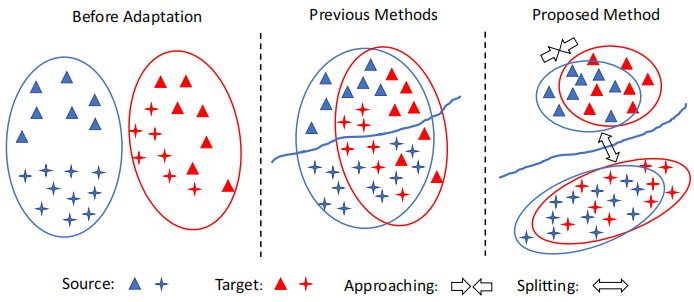
1 前言

　　例子：

　　

　　Left：在适应之前，源数据和目标数据之间存在域偏移；

　　Middle：类不可知的自适应在域级将源数据和目标数据对齐，忽略了样本的类标签，因此可能导致次优解。因此，一个标签的目标样本可能与不同标签的源样本不一致；

　　Right：本文执行跨域的类感知对齐。为了避免错位，只减少了类内域的差异。将类间域差异最大化，提高了模型的泛化能力。

2 相关工作

2.1 类无关对齐

　　MMD 距离（Maximum mean discrepancy)，度量在再生希尔伯特空间中两个分布的距离，是一种核学习方法。 两个随机变量的距离为：

　　　　$\operatorname{MMD}[\mathcal{F}, p, q] := \underset{f \in \mathcal{F}}{\text{sup}} \left(\mathbf{E}_{p}[f(x)]-\mathbf{E}_{q}[f(y)]\right)$

　　　　$\operatorname{MMD}[\mathcal{F}, X, Y] :=\underset{f \in \mathcal{F}}{\text{sup}}\left(\frac{1}{m} \sum\limits _{i=1}^{m} f\left(x_{i}\right)-\frac{1}{n} \sum\limits_{i=1}^{n} f\left(y_{i}\right)\right)$

　　理解：如果两个分布一样时，那么只要采样的样本足够多，那么不论函数域怎么定义，其 MMD 距离都是 $0$，因为不论通过什么样的函数映射后，两个一样的分布映射后的分布还是一样的，那么他们的期望之差都为 $0$ ，上界也就是 $0$。

　　MMD 的平方公式：

　　　　$\operatorname{MMD}[\mathcal{F}, X, Y]=\left[\frac{1}{m^{2}} \sum\limits _{i, j=1}^{m} k\left(x_{i}, x_{j}\right)-\frac{2}{m n} \sum\limits_{i, j=1}^{m, n} k\left(x_{i}, y_{j}\right)+\frac{1}{n^{2}} \sum\limits_{i, j=1}^{n} k\left(y_{i}, y_{j}\right)\right]^{\frac{1}{2}}$

　　在实际应用中，对于第 $l$ 层，MMD 的平方值是用经验核均值嵌入来估计的：

　　　　$\begin{aligned}\hat{\mathcal{D}}_{l}^{m m d} & =\frac{1}{n_{s}^{2}} \sum_{i=1}^{n_{s}} \sum_{j=1}^{n_{s}} k_{l}\left(\phi_{l}\left(\boldsymbol{x}_{i}^{s}\right), \phi_{l}\left(\boldsymbol{x}_{j}^{s}\right)\right) \\& +\frac{1}{n_{t}^{2}} \sum_{i=1}^{n_{t}} \sum_{j=1}^{n_{t}} k_{l}\left(\phi_{l}\left(\boldsymbol{x}_{i}^{t}\right), \phi_{l}\left(\boldsymbol{x}_{j}^{t}\right)\right) \\& -\frac{2}{n_{s} n_{t}} \sum_{i=1}^{n_{s}} \sum_{j=1}^{n_{t}} k_{l}\left(\phi_{l}\left(\boldsymbol{x}_{i}^{s}\right), \phi_{l}\left(\boldsymbol{x}_{j}^{t}\right)\right)\end{aligned}\quad\quad\quad(2)$

　　其中，$x^{s} \in \mathcal{S}^{\prime} \subset \mathcal{S}$，$x^{t} \in \mathcal{T}^{\prime} \subset \mathcal{T}$，$n_{s}=\left|\mathcal{S}^{\prime}\right|$，$n_{t}=\left|\mathcal{T}^{\prime}\right|$。$\mathcal{S}^{\prime}$ 和 $\mathcal{T}^{\prime}$ 分别表示从 $S$ 和 $T$ 中采样的小批量源数据和目标数据。$k_{l}$ 表示深度神经网络第 $l$ 层选择的核。

　　MMD 公式推导 

3 方法

3.1 对比域差异

　　CDD 明确地考虑类信息，并衡量跨域的类内和类间的差异。最小化类内域差异以压缩类内样本的特征表示，而最大以类间域差异使彼此的表示更远离决策边界。联合优化了类内和类间的差异，以提高了自适应性能。

　　所提出的对比域差异（CDD）是基于条件数据分布之间的差异。MMD 没有对数据分布的类型（例如边际或条件）的任何限制，MMD 可以方便地测量 $P\left(\phi\left(\boldsymbol{X}^{s}\right) \mid Y^{s}\right)$ 和 $Q\left(\phi\left(\boldsymbol{X}^{t}\right) \mid Y^{t}\right)$ 之间的差异：

　　　　$\mathcal{D}_{\mathcal{H}}(P, Q) \triangleq   \sup _{f \sim \mathcal{H}}\left(\mathbb{E}_{\boldsymbol{X}^{s}}\left[f\left(\phi\left(\boldsymbol{X}^{s}\right) \mid Y^{s}\right)\right]-\mathbb{E}_{\boldsymbol{X}^{t}}\left[f\left(\phi\left(\boldsymbol{X}^{t}\right) \mid Y^{t}\right)\right]\right)_{\mathcal{H}}$

　　假设：

　　　　$\mu_{c c^{\prime}}\left(y, y^{\prime}\right)=\left\{\begin{array}{ll}1 & \text { if } y=c, y^{\prime}=c^{\prime} \\0 & \text { otherwise }\end{array}\right.$

　　$\mathcal{D}_{\mathcal{H}}(P, Q)$ 核均值平方嵌入：

　　　　$ \hat{\mathcal{D}}^{c_{1} c_{2}}\left(\hat{y}_{1}^{t}, \hat{y}_{2}^{t}, \cdots, \hat{y}_{n_{t}}^{t}, \phi\right)=e_{1}+e_{2}-2 e_{3}   \quad \quad\quad(3) $

　　其中：

　　　　$\begin{aligned}e_{1} & =\sum_{i=1}^{n_{s}} \sum_{j=1}^{n_{s}} \frac{\mu_{c_{1} c_{1}}\left(y_{i}^{s}, y_{j}^{s}\right) k\left(\phi\left(\boldsymbol{x}_{i}^{s}\right), \phi\left(\boldsymbol{x}_{j}^{s}\right)\right)}{\sum_{i=1}^{n_{s}} \sum_{j=1}^{n_{s}} \mu_{c_{1} c_{1}}\left(y_{i}^{s}, y_{j}^{s}\right)} \\e_{2} & =\sum_{i=1}^{n_{t}} \sum_{j=1}^{n_{t}} \frac{\mu_{c_{2} c_{2}}\left(\hat{y}_{i}^{t}, \hat{y}_{j}^{t}\right) k\left(\phi\left(\boldsymbol{x}_{i}^{t}\right), \phi\left(\boldsymbol{x}_{j}^{t}\right)\right)}{\sum_{i=1}^{n_{t}} \sum_{j=1}^{n_{t}} \mu_{c_{2} c_{2}}\left(\hat{y}_{i}^{t}, \hat{y}_{j}^{t}\right)} \\e_{3} & =\sum_{i=1}^{n_{s}} \sum_{j=1}^{n_{t}} \frac{\mu_{c_{1} c_{2}}\left(y_{i}^{s}, \hat{y}_{j}^{t}\right) k\left(\phi\left(\boldsymbol{x}_{i}^{s}\right), \phi\left(\boldsymbol{x}_{j}^{t}\right)\right)}{\sum_{i=1}^{n_{s}} \sum_{j=1}^{n_{t}} \mu_{c_{1} c_{2}}\left(y_{i}^{s}, \hat{y}_{j}^{t}\right)}\end{aligned}   \quad \quad\quad(4) $

　　Note：1：当 $c_{1}=c_{2}=c$ 时，它测量类内域差异；2：当 $c_{1} \neq c_{2}$ 时，它成为类间域差异。

　　CDD 完整计算如下：

　　　　$\begin{aligned}\hat{\mathcal{D}}^{c d d} & =\underbrace{\frac{1}{M} \sum_{c=1}^{M} \hat{\mathcal{D}}^{c c}\left(\hat{y}_{1: n_{t}}^{t}, \phi\right)}_{\text {intra }} \\& -\underbrace{\frac{1}{M(M-1)} \sum_{c=1}^{M} \sum_{\substack{c^{\prime}=1 \\c^{\prime} \neq c}}^{M} \hat{\mathcal{D}}^{c c^{\prime}}\left(\hat{y}_{1: n_{t}}^{t}, \phi\right)}_{\text {inter }}\end{aligned} \quad \quad\quad(5) $

3.2 对比自适应网络

　　多层对比自适应损失：

　　　　$\hat{\mathcal{D}}_{\mathcal{L}}^{c d d}=\sum\limits_{l=1}^{L} \hat{\mathcal{D}}_{l}^{c d d}\quad \quad\quad(6) $

　　源域交叉熵：

　　　　$\ell^{c e}=-\frac{1}{n^{\prime}} \sum\limits _{i^{\prime}=1}^{n_{s}^{\prime}} \log P_{\theta}\left(y_{i^{\prime}}^{s} \mid \boldsymbol{x}_{i^{\prime}}^{s}\right)\quad \quad\quad(7) $

　　目标函数：

　　　　$\underset{\theta}{\text{min}}\quad   \ell=\ell^{c e}+\beta \hat{\mathcal{D}}_{\mathcal{L}}^{c d d}\quad \quad\quad(8) $

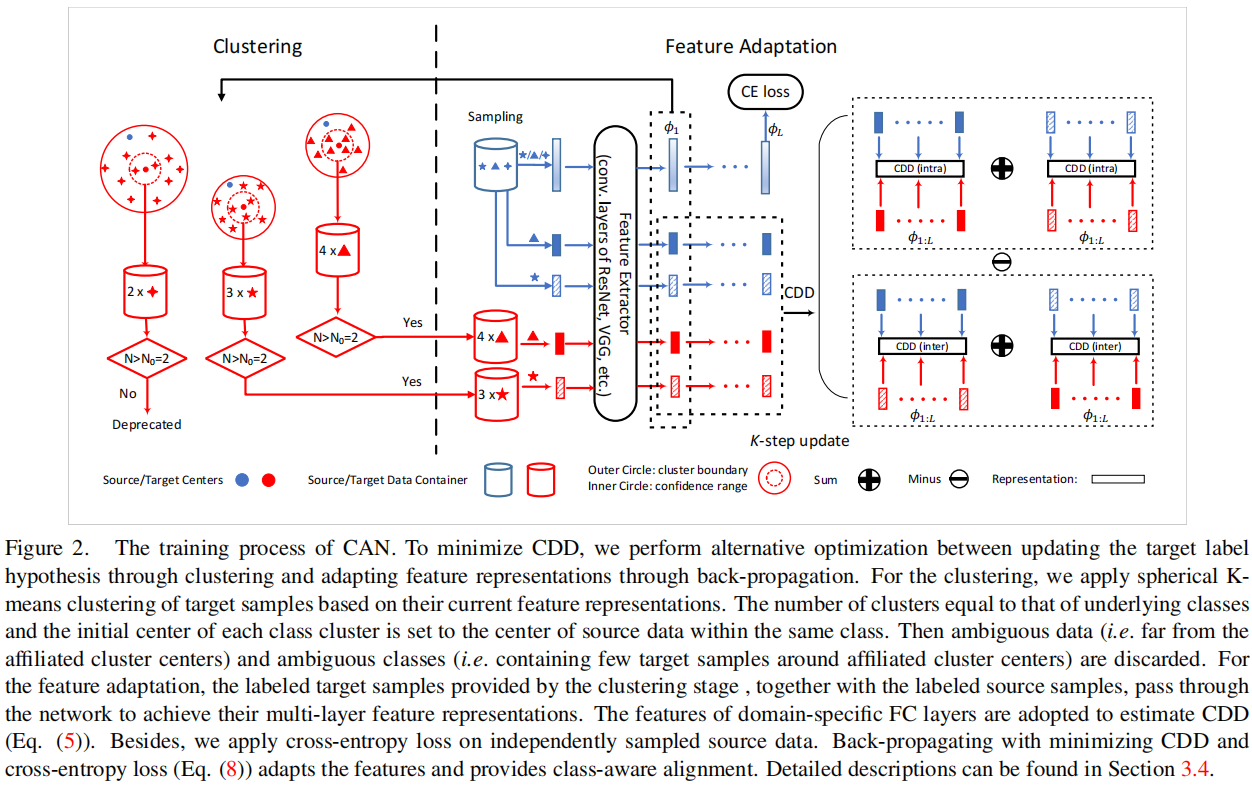
3.3 CAN 优化

3.3.1 CAN 的框架

　　

3.3.2 交替优化

　　步骤：

　　1）使用源域标签计算相应的类中心 $\mathrm{O}^{\mathrm{t}, \mathrm{c}}$ ：

　　　　$\mathrm{O}^{\mathrm{sc}}=\sum_{i=1}^{\mathrm{n}_{\mathrm{s}}} 1_{y_{i}^{\mathrm{s}}=\mathrm{c}} \frac{\phi_{1}\left(\mathrm{x}_{\mathrm{i}}^{\mathrm{s}}\right)}{\left.\| \mathrm{x}_{\mathrm{i}}\right) \|}$$

　　　　$1_{y_{\mathrm{i}}^{\mathrm{s}}=\mathrm{c}}=\left\{\begin{array}{ll}1 & \text { if } \mathrm{y}_{\mathrm{i}}^{\mathrm{s}}=\mathrm{c} ; \\0 & \text { otherwise. }\end{array}, \mathrm{c}=\{0,1, \ldots, \mathrm{M}-1\}\right.$

　　2）计算目标样本与类中心之间的距离：

　　　　$\operatorname{dist}(\mathrm{a}, \mathrm{b})=\frac{1}{2}\left(1-\frac{\mathrm{a} \cdot \mathrm{b}}{\|\mathrm{a}\|\|\mathrm{b}\|}\right) $

　　3）聚类更新：

　　　　(1) 对每个目标域的样本找到所对应的聚类中心: $\hat{y}_{\mathrm{i}}^{\mathrm{t}}=\underset{c}{\arg \min \operatorname{dist}}\left(\phi\left(\mathrm{x}_{\mathrm{i}}^{\mathrm{t}}\right), \mathrm{O}^{\mathrm{tc}}\right) $;

　　　　(2) 更新聚类中心: $\mathrm{O}^{\mathrm{tc}} \leftarrow \sum_{\mathrm{i}=1}^{\mathrm{N}_{\mathrm{t}}} 1_{\hat{y}_{\mathrm{i}}^{\mathrm{t}}=\mathrm{c}}\frac{\phi_{1}\left(\mathrm{x}_{\mathrm{t}}^{\mathrm{t}}\right)}{\left\|\phi_{1}\left(\mathrm{x}_{\mathrm{i}}\right)\right\|}$

　　迭代直到收敛或者抵达最大聚类步数停止；
　　4）聚类结束后，每个目标域的样本 $\mathrm{x}_{\mathrm{i}}^{\mathrm{t}}$ 被赋予一个标签 $ \hat{y}_{\mathrm{i}}^{\mathrm{t}}$；
　　5）设定一个阈值 $\mathrm{D}_{0} \in[0,1]$  ，将属于某个簇但是距离仍然超过给定阈值的数据样本删除，不参与本次计算 CDD，仅保留距离小于 $\mathrm{D}_{0}$ 的样本：

　　　　$\hat{\mathcal{T}}=\left(\mathrm{x}^{\mathrm{t}}, \hat{\mathrm{y}}^{\mathrm{t}}\right) \mid \operatorname{dist}\left(\phi_{1}\left(\mathrm{x}^{\mathrm{t}}\right), \mathrm{O}^{\mathrm{t}, \hat{\mathrm{y}}^{\mathrm{t}}}\right)<\mathrm{D}_{0}, \mathrm{x}^{\mathrm{t}} \in \mathcal{T}$

　　6）此外，为了提供更准确的样本分布的统计数据，假设每个类别挑选出来的集合 $ \hat{\mathcal{T}}$ 的大小至少包含某个数量 $N_{0}$ 的样本，不然这个类别本次也不参与计算 CDD，即最后参与计算的类别集为: 

　　　　$\mathcal{C}_{T_{e}}=\left\{c \mid \sum_{i}^{|\mathcal{T}|} \mathbf{1}_{\hat{y}_{i}^{t}=c}>N_{0}, c \in \{0,1, \cdots, M-1\} \right \}  $

　　算法如下：

　　

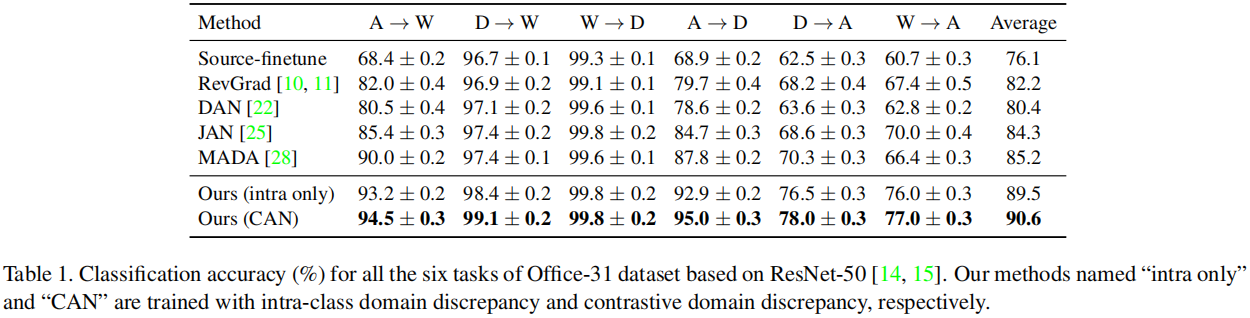
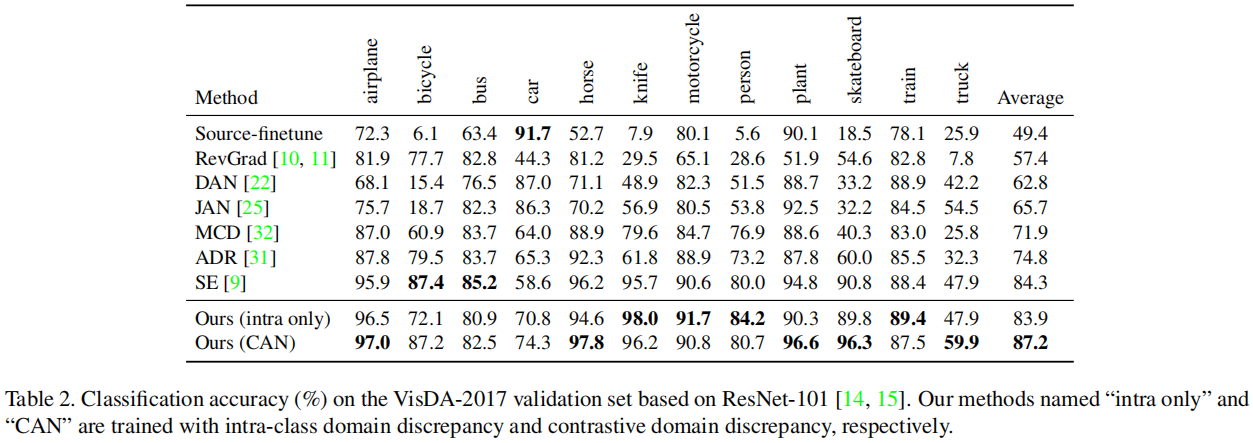
5 Experiment