虚假新闻检测（CANMD）《Contrastive Domain Adaptation for Early Misinformation Detection: A Case Study on COVID-19》

论文信息

论文标题：Contrastive Domain Adaptation for Early Misinformation Detection: A Case Study on COVID-19
论文作者：Zhenrui Yue, Huimin Zeng, Ziyi Kou, Lanyu Shang, Dong Wang
论文来源：2022 CIKM
论文地址：download 
论文代码：download

1 Introduction

　　对比域自适应。

2 Problem statement

　　Source data: Labeled source data from  $\boldsymbol{X}_{s}$. Each example  $\left(x_{s}, y_{s}\right) \in \mathcal{X}_{s}$  is defined by an input text  $x_{s}$  and a label  $y_{s}$ . We denote the joint distribution   $\left(x_{s}, y_{s}\right)$  in  $\boldsymbol{X}_{s}$  with  $\mathcal{P}$ .

　　Target data: Unlabeled target data from  $\boldsymbol{X}_{t}$ . For target example  $\left(x_{t}, y_{t}\right) \in \boldsymbol{X}_{t}$ , we only have access to the input text  $x_{t}$ . Ground truth label  $y_{t}$  is not given for training. Similarly, we denote the joint distribution in  $\boldsymbol{X}_{t}$  with  $Q$ .

　　Model: The classification model can be represented with function $f$ . $f$ takes text $x$ as input and yields output logits. The output probability distribution is obtained by using the softmax function $\sigma$ . Ideally, the model $f$ can correctly predict the ground truth $y$ with the maximum logit value, namely $y=\arg \max f(x)$ .

　　Objective: The objective is to adapt a classifier $f$ trained on source distribution $\mathcal{P}$ to the target distribution $Q$ , such that the performance can be maximized in the target data $\mathcal{X}_{t}$ . In other words, we minimize the negative log likelihood (NLL) loss between model output distribution $\sigma\left(f\left(x_{t}\right)\right)$ and ground truth $y_{t}$ for $\boldsymbol{X}_{t}$ :

　　　　$\min _{f} \mathbb{E}_{\left(x_{t}, y_{t}\right) \sim \chi_{t}} \mathcal{L}_{\mathrm{nll}}\left(\sigma\left(f\left(x_{t}\right)\right), y_{t}\right)\quad\quad(1)$

3 Method

　　为了使训练后的分类器适应于目标域，提出通过逼近目标联合分布的早期错误信息检测的对比自适应网络（CANMD）。与之前假设协变量偏移的工作不同，本文考虑了源域和目标域之间的标签偏移（即 $p(y) \neq q(y)$）和条件偏移（即 $p(x \mid y) \neq q(x \mid y)$）。由于 $ p(x, y)=p(x \mid y) p(y)$（类似地，$q(x, y)=q(x \mid y) q(y)$ ），我们调整错误信息检测模型 $f$ 到目标域的解决方案是双重的：(1) 标签位移估计和校正：我们对 $X_{t}$ 中的例子生成伪标签，并对标签进行重新缩放，以纠正由标签比例的位移引起的联合分布的位移。换句话说，我们估计并校正了 $q(y)$。(2) 条件分布自适应：利用上一步生成的伪标签，利用对比域自适应使条件分布 $p(x \mid y)$ 和 $q(x \mid y)$ 之间的距离最小化。当我们减小两个条件分布（即 $p(x \mid y) \approx q(x \mid y)$）之间的距离时，我们使用修正后的 $q(y)$ 改进了 $ q(x, y)=p(x \mid y) q(y)$ 的估计。

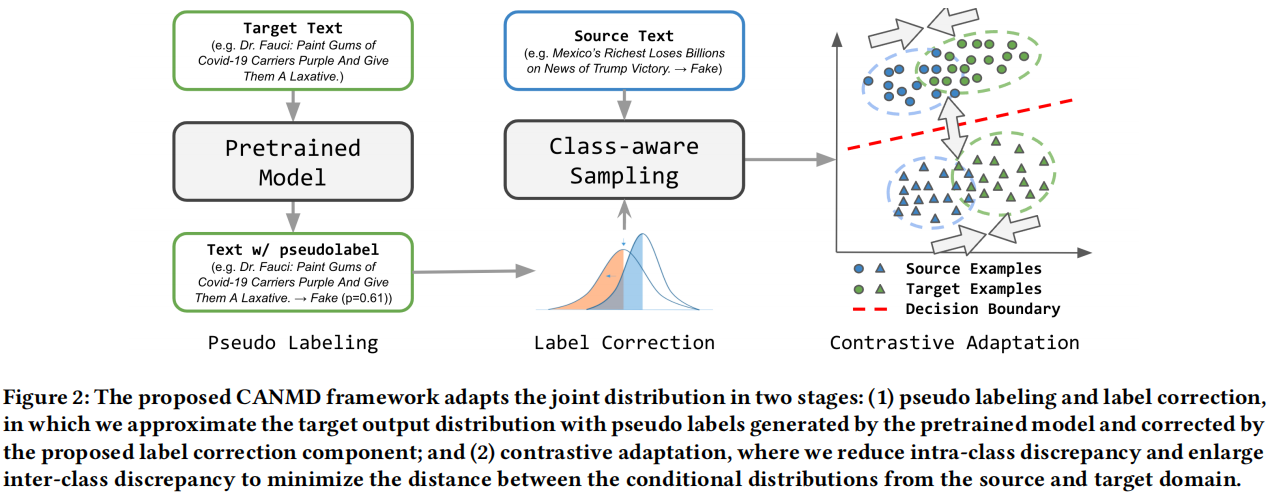
　　标签偏移修正的原因是 COVID-19 错误信息的动态快速变化。例如，社交媒体平台上的错误信息的比例在不同的阶段（即标签转移）的中迅速发生变化。此外，传统的错误信息检测系统由于巨大的领域差异，往往无法识别 COVID 错误信息。因此，提出的 CANMD 包括两个阶段： (1) 伪标记和标签校正，我们在目标域进行伪标记和纠正标签分布 $q(y)$；(2) 对比自适应，减少了类内差异，扩大了两个领域的例子之间的类间差异。通过利用第一阶段的伪标签，我们估计并最小化条件分布 $p(x|y)$ 和 $q(x|y)$ 之间的差异。Figure 2 提供了 CANMD 的说明，与现有的方法不同，我们建议纠正标签位移并适应条件分布，而不是仅仅减少特征差异。

　　

3.1 Pseudo Labeling and Label Correction

　　鉴于对标记源数据 $\mathcal{X}_{s}$ 的访问，我们首先对错误信息分类系统进行预训练。在实践中，如果模型已经对源数据进行了训练，我们可以跳过这一步。一旦源训练的模型准备好，我们将使用 $\arg \max f\left(x_{t}\right)$ 生成未标记的目标示例 $x_{t}$ 的伪标签 $\hat{y}_{t}$。

　　然而，生成的伪标签是有噪声的，这往往会导致域自适应性能的下降，特别是当存在较大的域间隙时。此外，两个域之间不同的标签比例（即标签的移位）会导致有偏倚的伪标签和潜在的负转移结果[1]。受校准方法[11]的启发，我们提出了一个标签校正分量来校正伪标签与目标输出分布之间的分布偏移。特别对于输入 $x$，我们设计向量缩放，引入可学习参数 $w$ 和 $b$，并计算校正后的输出如下：

　　　　$\sigma(\boldsymbol{w} \odot f(x)+b)\quad\quad(2)$

　　其中，$\odot$ 表示元素级乘积，$\sigma$ 表示 softmax 函数。在极少数情况下，当源和目标输出分布导致 $b$ 中产生较大的偏差值时，我们丢弃偏差 $b$ 以避免产生恒定输出概率（即 $b$ 时（$\sigma(\boldsymbol{w} \odot   f(x)+b) \approx \sigma(b) $ 当 $b$ 包含远远大于 $w \odot f(x)$ 的值时）。因此，该校正方法可简化为：

　　　　$\sigma(w \odot f(x))\quad\quad(3)$

　　为了得到优化的 $w$ 和 $b$，我们在训练中优化了参数 $w$ 和 $b$，以重新调整输出概率并拟合分布 $q(y)$。给定预先训练的错误信息检测函数 $f$ 和输入对 $\left(x_{t}, y_{t}\right)$，我们遵循[11]并最小化 NLL 损失：

　　　　$ \underset{\boldsymbol{w}, \boldsymbol{b}}{\text{min}} \;\;  \mathbb{E}_{\left(\boldsymbol{x}_{t}, y_{t}\right) \sim \boldsymbol{X}_{t}} \quad \mathcal{L}_{\mathrm{nll}}\left(\sigma\left(\boldsymbol{w} \odot \boldsymbol{f}\left(\boldsymbol{x}_{t}\right)+\boldsymbol{b}\right), y_{t}\right)\quad\quad(4)$

　　在输出概率恒定或优化失败的情况下，$b$ 被丢弃。与之前工作类似，验证集用于优化向量重缩放参数。

　　综上所述，通过标签校正成分进行的伪标签和标签校正阶段可以表述为：

　　　　$\hat{y}_{t}=\arg \max \sigma(\boldsymbol{w} \odot f(x)+\boldsymbol{b})\quad\quad(5)$

　　经过标签校正后，我们对伪标签进行过滤，选择目标样本的一个子集进行对比自适应。根据标签置信度（即 $ \max \sigma(\boldsymbol{w} \odot f(x)+\boldsymbol{b})$）对伪标签进行过滤，如果置信值高于置信阈值 $\tau$，我们保留目标样本。下面，我们使用 $\chi _{t}^{\prime}$ 用伪标签表示过滤后的目标数据。通过引入标签校正成分，我们减少了当源标签分布和目标标签分布发生偏移时，来自 $f$ 的偏差。例如，CoAID数据集中的COVID错误信息包含不到10%的虚假声明[4]。如果 $f$ 在平衡数据集上进行预训练，无论 CoAID 中的标签分布如何，伪标签都会显示相似的标签分布，并导致噪声标签。CANMD 使用可学习参数来调整模型输出，然后使用置信度阈值，从目标相似分布中选择高置信度样本。

3.2 Contrastive Adaptation

　　现在描述 CANMD 的对比适应阶段。我们执行小批量训练，并从源数据 $\boldsymbol{X}_{s}$ 和标记的目标数据 $\boldsymbol{X}_{t}^{\prime}$ 中采样相同数量的输入对$(x,y)$。为了近似目标数据分布并有效地估计差异，我们采用了类感知抽样策略，以保证每个类内的样本数量相同。具体来说，首先从目标数据 $\boldsymbol{X}_{t}^{\prime}$ 中采样目标批。通过计算目标批处理中的示例，我们分别从每个源数据 $\boldsymbol{X}_{s}$ 中抽取相同数量的每个类中抽取相同数量的示例。因此，我们构建了两个域中由相同类和相同数量示例组成的小批。我们也类似于目标数据的分布，并在自适应[17]过程中加入了源域知识。

　　为了估计域差异，我们重新访问最大平均差异（MMD）距离。MMD 使用从它们中提取的样本来估计两个分布之间的距离。

　　给定 $\mathcal{P}$ 和 $\mathcal{Q}$，MMD 距离定义如下：

　　　　$\mathcal{D}=\sup _{f \in \mathcal{H}}\left(\mathbb{E}_{x \sim \mathcal{P}}[f(x)]-\mathbb{E}_{y \sim Q}[f(y)]\right) ]\quad\quad(6)$

　　其中，$f$ 是再现核希尔伯特空间 $\mathcal{H}$ 的一个函数（核）。通过引入核技巧和经验核平均嵌入[28,55]，我们进一步简化了 $\boldsymbol{X}_{s}$ 和 $\boldsymbol{X}_{t}^{\prime}$ 之间的平方 MMD 距离的估计如下：

　　　　$\begin{aligned}\mathcal{D}^{\mathrm{MMD}} & =\frac{1}{\left|\boldsymbol{X}_{s}\right|\left|\boldsymbol{X}_{s}\right|} \sum_{i=1}^{\left|\boldsymbol{X}_{s}\right|} \sum_{j=1}^{\left|\boldsymbol{X}_{s}\right|} k\left(\phi\left(\boldsymbol{x}_{s}^{(i)}\right), \phi\left(\boldsymbol{x}_{s}^{(j)}\right)\right)\\& +\frac{1}{\left|\boldsymbol{X}_{t}^{\prime}\right|\left|\boldsymbol{X}_{t}^{\prime}\right|} \sum_{i=1}^{\left|X_{t}^{\prime}\right|} \sum_{j=1}^{ |X_{t}^{\prime}|} k  \left(\phi\left(x_{t}^{\prime(i)}\right), \phi\left(x_{t}^{\prime(j)}\right)\right)\\& -\frac{2}{\left|\mathcal{X}_{s}\right|\left|X_{t}^{\prime}\right|} \sum_{i=1}^{\left|X_{s}\right|} \sum_{j=1}^{\left|X_{t}^{\prime}\right|} k\left(\phi\left(x_{s}^{(i)}\right), \phi\left(x_{t}^{(j)}\right)\right)\end{aligned}\quad\quad(7)$

　　其中，我们采用 transformer 模型中 [CLS] 位置的输出作为 $\phi$。$k$ 为高斯核，即 $k\left(x_{i}, x_{j}\right)=\exp \left(-\frac{\left\|x_{i}-x_{j}\right\|^{2}}{\gamma}\right)$。估计的 MMD 距离用于计算对比自适应损失。特别地，我们利用 $\text{Eq.7}$ 来规范在同一类内的示例和来自不同类内的示例之间的距离。为此目的，我们将具有类感知能力的MMD 定义为：

　　　　${\large \begin{array}{l}\mathcal{D}_{\mathrm{c}_{1} \mathrm{c}_{2}}^{\mathrm{MMD}}=&\sum_{i=1}^{\left|\boldsymbol{X}_{s}\right|} \sum_{j=1}^{\left|X_{s}\right|} \frac{\mathbb{1}_{c_{1} c_{2}}\left(y_{s}^{(i)}, y_{s}^{(j)}\right) k\left(\phi\left(x_{s}^{(i)}\right), \phi\left(x_{s}^{(j)}\right)\right)}{\sum_{l=1}^{\left|X_{s}\right|} \sum_{m=1}^{\left|X_{s}\right|} \mathbb{1}_{c_{1} c_{2}}\left(y_{s}^{(l)}, y_{s}^{(m)}\right)} \\&+\sum_{i=1}^{\left|X_{t}^{\prime}\right|} \sum_{j=1}^{|X_{t}^{\prime}|} \frac{\mathbb{1}_{c_{1} c_{2}}\left(y_{t}^{\prime(i)}, y_{t}^{\prime(j)}\right) k\left(\phi\left(x_{t}^{(i)}\right), \phi\left(x_{t}^{\prime(j)}\right)\right)}{\sum_{l=1}^{\left|X_{t}^{\prime}\right|} \sum_{m=1}^{\left|X_{t}^{\prime}\right|} \mathbb{1}_{c_{1} c_{2}}\left(y_{t}^{\prime(l)}, y_{t}^{\prime(m)}\right)} \\&-2 \sum_{i=1}^{\left|X_{s}\right|} \sum_{j=1}^{\left|X_{t}^{\prime}\right|} \frac{\mathbb{1}_{c_{1} c_{2}}\left(y_{s}^{(i)}, y_{t}^{\prime(j)}\right) k\left(\phi\left(x_{s}^{(i)}\right), \phi\left(x_{t}^{\prime(j)}\right)\right)}{\sum_{l=1}^{\left|X_{s}\right|} \sum_{m=1}^{\left|X_{t}^{\prime}\right|} \mathbb{1}_{c_{1} c_{2}}\left(y_{s}^{(l)}, y_{t}^{\prime(m)}\right)} \\\end{array}}\quad\quad(8)$

　　其中，$\mathbb{1}_{c_{1} c_{2}}\left(y_{1}, y_{2}\right)=\left\{\begin{array}{l}1, \text { if } y_{1}=c_{1}, y_{2}=c_{2} \\0, \text { else }\end{array}\right.$，$c_{1}$、$c_{2}$ 代表着两个类，如果 $c_{1}$ 和 $c_{2}$ 是相同的类，那么 $\mathcal{D}_{\mathrm{c}_{1} \mathrm{c}_{2}}^{\mathrm{MMD}}$ 估计源域和目标域之间的类内差异，如果 $c_{1}$ 和 $c_{2}$ 不是相同的类，那么 $\mathcal{D}_{\mathrm{c}_{1} \mathrm{c}_{2}}^{\mathrm{MMD}}$ 估计源域和目标域之间的类间差异。利用类感知的 MMD 距离，我们将对比损失量定义为优化目标的一部分：

　　$\mathcal{L}_{\text {contrasive }}=\mathcal{D}_{00}^{\mathrm{MMD}}+\mathcal{D}_{11}^{\mathrm{MMD}}-\frac{1}{2}\left(\mathcal{D}_{01}^{\mathrm{MMD}}+\mathcal{D}_{10}^{\mathrm{MMD}}\right)\quad\quad(9)$

　　当我们在错误信息检测中考虑二元分类时，$\mathcal{D}_{00}^{M M D}$ 和 $\mathcal{D}_{11}^{M M D}$ 是指表示空间中错误信息示例和可信例的类内差异。$\mathcal{D}_{01}^{M M D}+ \mathcal{D}_{10}^{M M D}$ 表示类间的差异，扩大不同类之间的距离，避免错误分类（取负值）。基于类内和类间差异的结合，错误信息检测系统 $f$ 学习了一个特征表示，将来自不同类的输入分离出来，并混淆来自同一类的输入。

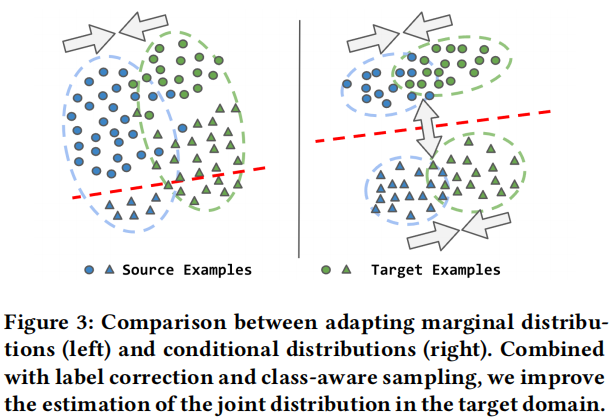
　　换句话说，损失将同一类样本聚集在一起，来自不同类的示例被分开。因此，我们基于前一阶段生成的伪标签，最小化了 $p(x \mid y)$ 和 $q(x \mid y)$ 之间的距离，我们在Figure 3 中说明了自适应过程。当源域和目标域之间存在标签转移时，适应边缘分布的现有方法（左图）可能会导致性能下降（参见绿色三角形）。与这些方法相反，CANMD（右）修正了目标分布中的标签位移和样本，以适应条件分布，从而产生了一个改进的目标域的决策边界。

　　

　　通过结合分类的 NLL 损失和上述对比损失，我们在我们的对比适应阶段的总体优化目标如下：

　　　　$\mathcal{L}=\mathcal{L}_{\text {nll }}+\lambda \mathcal{L}_{\text {contrasive }}\quad\quad(10)$

　　其中 $\mathcal{L}_{\text {nll }}$ 整合了来自源域和目标域的知识（通过伪标签），而 $\mathcal{L}_{\text {contrasive }}$ 将条件分布适应到目标域。$\lambda$ 可以根据经验来选择。

3.3 Overall Framework

　　CANMD的总体框架如图2所示。在伪标记和标签校正阶段，首先使用预先训练好的错误信息检测系统 $f$ 对所有目标示例生成伪标签。接下来，我们优化可学习的校正参数并对生成的伪标签进行校正，我们还使用最小置信阈值 $\tau$（根据经验选择）对目标数据进行过滤。在对比自适应阶段，我们执行类感知采样，以类似于目标数据 $f$ 的分布。然后，我们计算了一个对比自适应损失，以减少类内差异，扩大类间差异。对于每个时期，优化过程在 算法1 中被描述。

　　

　　与以往在文本分类[8,23,59]中的领域自适应工作不同，我们放弃了域对抗训练来有效训练，并近似目标域的联合分布。特别地，我们提出了一个标签校正组件来校正伪标记过程中对 $q(y)$ 的估计。这对应于对COVID错误信息中的伪标签的修正，其中我们消除了预训练模型中的潜在偏差，以减少自适应中的噪声标签。接下来，通过 MMD 距离最小化条件分布之间的距离来适应模型，其中模型学习领域混淆但类分离的特征。简单地说，我们通过特征空间中的细粒度对齐，将知识从源错误信息数据转移到 COVID 域。通过估计 $q(y)$ 和自适应关联模型 $p(x \mid y) \approx q(x \mid y)$，改进了 $q(x, y)=p(x \mid y) q(y)$ 的估计，从而提高了COVID-19错误信息检测的自适应性能。

4 EXPERIMENT

Datasets

　　

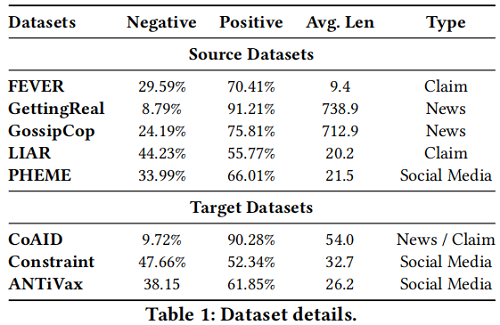
　　Note：Negative 和 Positive 分别是数据集中错误信息和有效信息的比例。

Model：根据[23,25,59]，我们选择常用的 RoBERTa 作为错误信息检测模型来执行所提出的 CANMD。RoBERTa 是一种基于 transformer 的语言模型，采用了改进的预训练方法，提高了各种 NLP 下游任务的性能。

Baselines：首先，将预先训练好的错误信息检测模型作为基线，直接对目标测试数据进行评估。我们另外选择了两个最先进的基线： DAAT 和 EADA [8,59]。DAAT 利用 BERT 的后期训练来改进领域的对抗性适应。EADA 使用一个额外的自动编码器来执行基于能量的对抗性域自适应。

Evaluation: 与[20,23,59]类似，我们将数据分成训练集、验证集和测试集和测试集 （7:1:2）。我们采用 accuracy 和 F1 score 来进行评价。此外，我们还引入了balanced accuracy（BA）来等价地评估这两类的自适应性能，BA 被定义为灵敏度和特异性的平均值：

　　　　$\mathrm{BA}=\frac{1}{2}(\mathrm{TPR}+\mathrm{TNR})=\frac{1}{2}\left(\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}+\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}}\right)\quad\quad(11)$

Implementation：1、special symbols like emojis are back translated into English words; 2、hashtags, mentions and URLs are tokenized for posts on social media; 3、special characters are removed from the input text.

Quantitative Analysis

　　

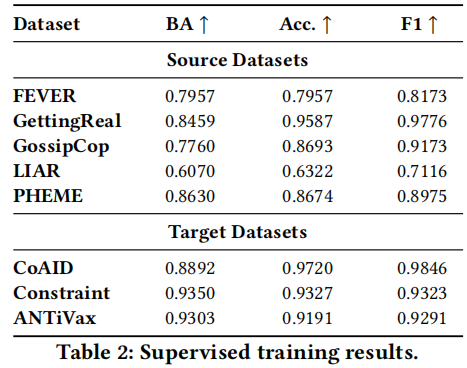
　　首先在 Table 2 中给出了所有数据集的监督训练结果，在目标数据集上的评估结果提供了自适应性能的上界。

　　(1) the performance varies for different data types. For example, RoBERTa does not perform well when we train on claims without additional knowledge (e.g., LIAR provides short claims). Predicting misinformation on social media posts achieves better performance with average BA of 0.9094 (i.e., PHEME, Constraint and ANTiVax), potentially due to the syntactic patterns of misinformation (e.g., second-person pronouns, swear words and adverbs [23]).

　　(2) For disproportionate label distributions, balanced accuracy (BA) better reflects the classification performance by weighting both classes equally. For example, the classification accuracy is 0.9587 on GettingReal, while the BA score drops drastically to 0.8459. This is because the dataset contains overwhelmingly true examples and by only predicting one class, the model still achieves over 0.9 accuracy. Overall, the supervised performance depends heavily on the input data type and label distributions, suggesting the potential benefits of domain similarity in adapting misinformation detection systems

现在我们研究了自适应性能，并将结果报告在 Table 3 中。

　　

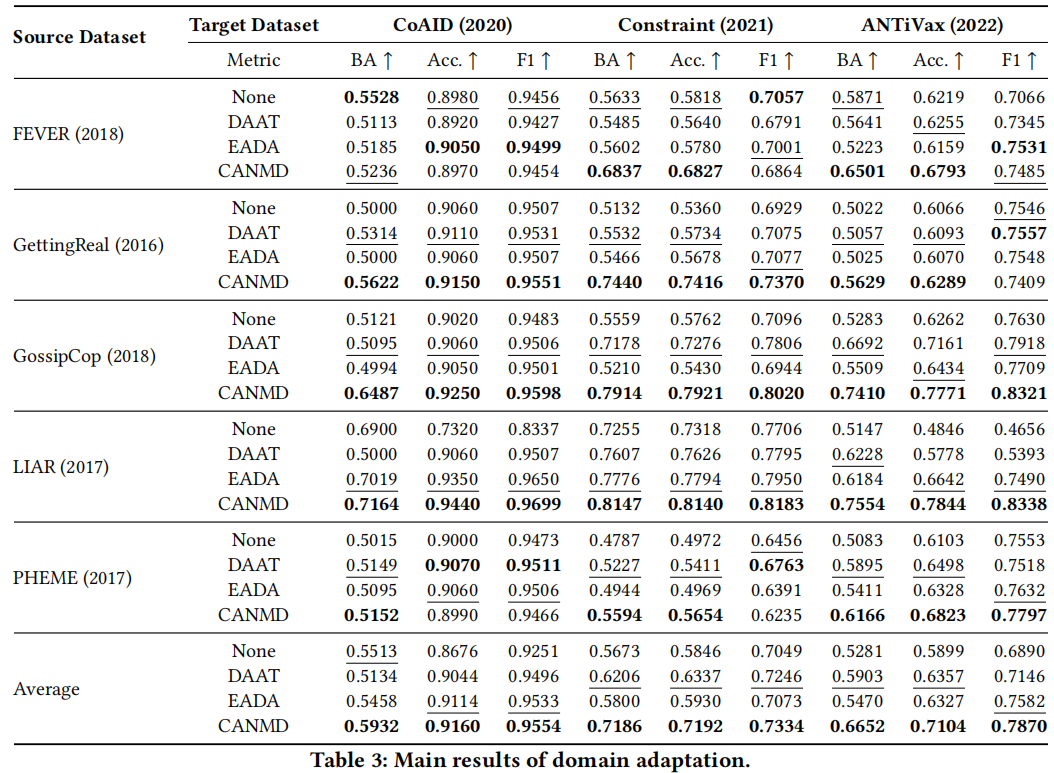
1. due to the large domain discrepancies, domain adaptation for COVID misinformation detection is a non-trivial task. For instance, the naïve baseline (i.e., None) trained on FEVER achieves 0.5633 BA and 0.5818 accuracy in Constraint;
2. in rare cases, we observe negative transfer. For example, consistent performance drops can be found on the BA metric in FEVER → CoAID experiments due to the discrepancy and the label shift across both domains.
3. Baseline adaptation methods achieve superior results than the naïve baseline (i.e., None) in most cases. For example, the DAAT baseline achieves 4.7% and 6.4% relative improvements on BA and accuracy, similar improvements can be found using EADA.
4. On average, CANMD performs the best by achieving the highest performance in most scenarios and outperforming the best baseline method by 11.5% and 7.9% on BA and accuracy.
5. CANMD performs well even when the source and target datasets demonstrate significant label shifts. For instance, GettingReal consists of over 90% true examples while Constraint is a balanced dataset in the COVID domain. CANMD achieves 0.7440 BA and 0.7416 accuracy in GettingReal → Constraint, with 34.5% and 29.3% improvements compared to the strongest baseline (i.e., DAAT).