虚假新闻检测（MAC）《Hierarchical Multi-head Attentive Network for Evidence-aware Fake News Detection》

论文信息

论文标题：Hierarchical Multi-head Attentive Network for Evidence-aware Fake News Detection
论文作者：Nguyen Vo, Kyumin Lee
论文来源：2021 EACL
论文地址：download 
论文代码：download

1 Introduction

　　现有的基于证据的虚假新闻检测要么关注与词级注意力，要么关注于证据级的注意力，这将导致一个次优的结果。本文提出了一个联合结合了多头词级注意和多头文档级注意，这有助于词级和证据级的解释。

　　贡献：

• • 提出了一种新的层次多头注意网络，将词注意和证据注意联合用于证据感知假新闻检测；
  • 提出了一种新的多头注意机制来捕捉重要的单词和证据；

2 Problem Statement

　　We denote an evidence-based fact-checking dataset  $\mathcal{C}$  as a collection of tuples  $(c, s, \mathcal{D}, \mathcal{P})$  where  $c$  is a textual claim originated from a speaker  $s$, $\mathcal{D}=   \left\{d_{i}\right\}_{i=1}^{k}$  is a collection of  $k$  documents  relevant to the claim  $c$  and  $\mathcal{P}=\left\{p_{i}\right\}_{i=1}^{k}$  is the corresponding publishers of documents in  $\mathcal{D}$ . Note,  $|\mathcal{D}|=|\mathcal{P}|$ . Our goal is to classify each tuple  $(c, s, \mathcal{D}, \mathcal{P})$  into a pre-defined class (i.e. true news/fake news).

3 Framework

框架：

　　

　　(1) embedding layer, (2)multi-head word attention layer, (3) multi-head document attention layer and (4) output layer.

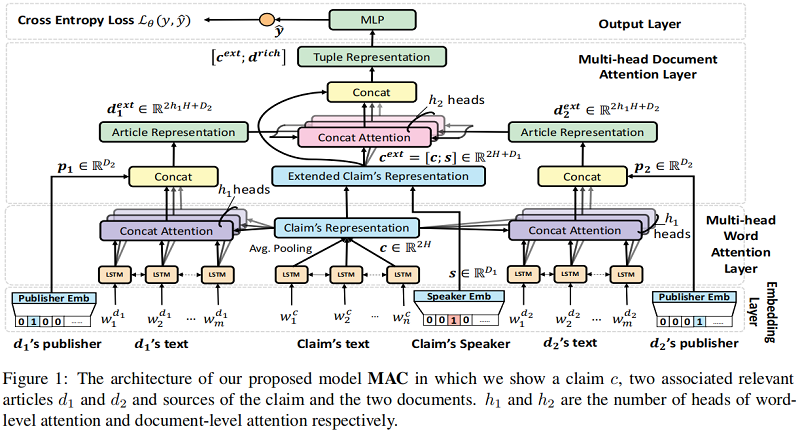
3.1 Embedding Layer

　　Each claim  $c$  is modeled as a sequence of  $n$  words  $\left[w_{1}^{c}, w_{2}^{c}, \ldots, w_{n}^{c}\right]$  and  $d_{i}$  is viewed as another sequence of  $m$  words  $\left[w_{1}^{d}, w_{2}^{d}, \ldots, w_{m}^{d}\right]$ . Each word  $w_{i}^{c}$  and  $w_{j}^{d}$  will be projected into D-dimensional vectors  $\mathbf{e}_{i}^{c}$  and  $\mathbf{e}_{j}^{d}$  respectively by an embedding matrix  $\mathbf{W}_{e} \in \mathbb{R}^{V \times D}$  where  $V$  is the vocabulary size. Each speaker  $s$  and publisher  $p_{i}$  modeled as one-hot vectors are transformed into dense vectors  $\mathbf{s} \in \mathbb{R}^{D_{1}}$  and  $\mathbf{p}_{i} \in \mathbb{R}^{D_{2}}$  respectively by using two matrices  $\mathbf{W}_{s} \in \mathbb{R}^{S \times D_{1}}$  and  $\mathbf{W}_{p} \in \mathbb{R}^{P \times D_{2}}$ , where  $S$  and  $P$  are the number of speakers and publishers in a training set respectively. Both  $\mathbf{W}_{s}$  and  $\mathbf{W}_{p}$  are uniformly initialized in  $[-0.2,0.2]$ . Note that, both matrices  $\mathbf{W}_{s}$  and  $\mathbf{W}_{p}$  are jointly learned with other parameters of our MAC.

3.2 Multi-head Word Attention Layer

　　将 claim 的词嵌入 $\mathbf{e}_{i}^{c}$ 送入 BiLSTM，生成文本表示 $\mathbf{h}_{i}^{c}=\left[\overleftarrow{\mathbf{h}_{i}} ; \overrightarrow{\mathbf{h}_{i}}\right] \in \mathbb{R}^{2 H}$，将生成的文本表示做平均池化 ：

　　　　$\mathbf{c}=\frac{1}{n} \sum\limits _{i=1}^{n} \mathbf{h}_{i}^{c} \quad\quad(1)$

　　对 Evidence 使用 BiLSTM，得到 $\mathbf{h}_{j}^{d} \in \mathbb{R}^{2 H}$，将其词嵌入表示为 矩阵形式 $\mathbf{H}=\left[\mathbf{h}_{1}^{d} \oplus \mathbf{h}_{2}^{d} \oplus \ldots \oplus \mathbf{h}_{m}^{d}\right] \in \mathbb{R}^{m \times 2 H}$。

　　为了理解文档中的信息帮助我们对 Claim 进行事实核查，我们需要指导我们的模型关注文档中的关键字或短语。我们首先复制向量 $c $ ($Eq.1$) $m$ 次创建矩阵 $\mathbf{C}_{1} \in \mathbb{R}^{m \times 2 H}$，并提出一种注意机制，具体如下：

　　　　$\mathbf{a}_{1}=\operatorname{softmax}\left(\tanh \left(\left[\mathbf{H} ; \mathbf{C}_{1}\right] \cdot \mathbf{W}_{1}\right) \cdot \mathbf{w}_{2}\right)\quad\quad(2)$

　　其中，$\mathbf{w}_{2} \in \mathbb{R}^{a_{1}}$，$\mathbf{W}_{1} \in \mathbb{R}^{4 H \times a_{1}}$，$\mathbf{a}_{1} \in \mathbb{R}^{m}$ 是在 $m$ 个单词上的注意力分布。

　　然而，文档的总体语义可能由文档的多个部分生成。因此，我们提出一个多头词注意机制，通过将向量 $w_2$ 扩展到矩阵 $\mathbf{W}_{2} \in \mathbb{R}^{a_{1} \times h_{1}}$ 来捕获不同的语义贡献，其中 $h_1$ 为 Figure 1 所示的注意头数。修改 $\text{Eq.2}$ 具体内容如下：

　　　　$\mathbf{A}_{1}=\operatorname{softmax}_{c o l}\left(\tanh \left(\left[\mathbf{H} ; \mathbf{C}_{1}\right] \cdot \mathbf{W}_{1}\right) \cdot \mathbf{W}_{2}\right)\quad\quad(3)$

　　其中，$\mathbf{A}_{1} \in \mathbb{R}^{m \times h_{1}}$，$\mathbf{A}_{1}$ 代表在文档 $d_i$ 中的 $m$ 个单词之上的 $h_1$ 不同的注意力分布，帮助我们捕获文档的不同方面。

　　在计算了 $\mathbf{A}_{1}$ 后 ，我们推导出文档 $d_i$ 的表示方式如下：

　　　　$\mathbf{d}_{i}=\operatorname{flatten}\left(\mathbf{A}_{1}^{T} \cdot \mathbf{H}\right)\quad\quad(4)$

　　其中，$\mathbf{d}_{i} \in \mathbb{R}^{h_{1} 2 H}$。

3.3 Multi-head Document Attention Layer

Extending representations of claims

　　spearker 有的时候非常重要，因此将其考虑入 claim ：

　　　　$\mathbf{c}^{e x t}=[\mathbf{c} ; \mathbf{s}] \in \mathbb{R}^{x}  \quad\quad(5)$

　　其中，$x = 2 H+D_{1}$。

Extending representations of evidence

　　同样 publisher 对于 Evidence 的真实性也有很大的帮助，所以：

　　　　$\mathbf{d}_{i}^{e x t}=\left[\mathbf{d}_{i} ; \mathbf{p}_{i}\right] \in \mathbb{R}^{y} \quad\quad(6)$

　　其中，$y= 2 h_{1} H+D_{2}$。

　　从 $\text{Eq.6}$ 开始，我们可以生成 $k$ 个相关文章的表示，并堆栈，如 $\text{Eq.7}$ 所示：

　　　　$\mathbf{D}=\left[\mathbf{d}_{1}^{e x t} \oplus \ldots \oplus \mathbf{d}_{k}^{e x t}\right] \in \mathbb{R}^{k \times y}\quad\quad(7)$

3.4 Multi-head Document Attention Mechanism

　　即使选择了 $k$ 个最相关的文章来判别 claim $c$ 的真实性，但是实际上往往只有个别几篇文章被用于判断 claim $c$ 的真实性，所以本文再一次使用注意力机制来选择合适的 documnet。

　　首先通过将 $\mathbf{c}^{e x t}$ 复制 $k$ 次，得到 $\mathbf{C}_{2} \in \mathbb{R}^{k \times x}$，然后将其与 $D$ ($\text{Eq.7}$) 拼接得到 $\left[\mathbf{D} ; \mathbf{C}_{2}\right] \in \mathbb{R}^{k \times(x+y)}$。

　　我们提出的多头文档级注意机制应用了 $h_2$ 个不同的注意头，如 $\text{Eq.8}$ 所示：

　　　　$\mathbf{A}_{2}=\operatorname{softmax}_{c o l}\left(\tanh \left(\left[\mathbf{D} ; \mathbf{C}_{2}\right] \cdot \mathbf{W}_{3}\right) \cdot \mathbf{W}_{4}\right)$

　　其中，$\mathbf{W}_{3} \in \mathbb{R}^{(x+y) \times a_{2}}$、$\mathbf{W}_{4} \in \mathbb{R}^{a_{2} \times h_{2}}$、$\mathbf{A}_{2} \in \mathbb{R}^{k \times h_{2}}$ 。

　　使用注意权重，我们可以生成  $k$ 个证据的参与表示，表示为 $\mathbf{d}^{r i c h} \in \mathbb{R}^{h_{2} y}$，如 $\text{Eq.9}$ 所示：

　　　　$\mathbf{d}^{\text {rich }}=\operatorname{flatten}\left(\mathbf{A}_{2}^{T} \cdot \mathbf{D}\right)\quad\quad(9)$

3.5 Output Layer

　　将 $ \left[\mathbf{c}^{e x t} ; \mathbf{d}^{\text {rich }}\right]$ 作为 MLP 的输入，计算 claim 真实性的概率：

　　　　$\hat{y}=\sigma\left(\mathbf{W}_{6} \cdot\left(\mathbf{W}_{5} \cdot\left[\mathbf{c}^{\text {ext }} ; \mathbf{d}^{\text {rich }}\right]+\mathbf{b}_{5}\right)+\mathbf{b}_{6}\right)\quad\quad(10)$

　　采用交叉熵优化模型：

　　　　$\mathcal{L}_{\theta}(y, \hat{y})=-(y \log \hat{y}+(1-y) \log (1-\hat{y}))\quad\quad(11)$

4 Experiment

Datasets

　　

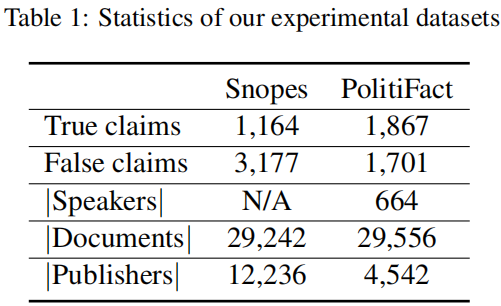
　　Note：Each Snopes claim was labeled as true or false while in Politifact, there were originally six labels: true, mostly true, half true, false, mostly false, pants on fire. Following (Popat et al., 2018), we merge true, mostly true and half true into true claims and the rest are into false claims.

Baselines

　　Using only claims’ text:

• • BERT
  • LSTM-Last
  • LSTM-Avg
  • CNN

　　Using both claims’ text and articles’ text

• • DeClare
  • HAN
  • NSMN

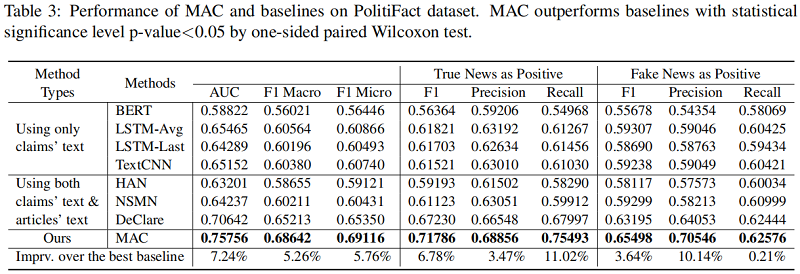
Performance of MAC and baselines