谣言检测（）《Data Fusion Oriented Graph Convolution Network Model for Rumor Detection》

论文信息

论文标题：Data Fusion Oriented Graph Convolution Network Model for Rumor Detection
论文作者：Erxue Min, Yu Rong, Yatao Bian, Tingyang Xu, Peilin Zhao, Junzhou Huang,Sophia Ananiadou
论文来源：2020,IEEE Transactions on Network and Service Management
论文地址：download 
论文代码：download

1 Introduction

　　本文不仅考虑了用户的基本信息和文本内容等静态特征，还考虑了谣言传播关系等动态特征。我们还对特征融合模块和池化模块进行了优化，使模型具有更好的性能。

　　本文贡献：

• • Considering the real dataset from social media, we extract static features such as users’ basic information and text contents, as well as dynamic features such as rumor propagation relations, and propose the data fusion method.
  • GCN is introduced into the rumor detection task, which represents the rumor propagation mode. And we propose to select the suitable graph convolution operator to update the node vectors, and improve the feature fusion and pooling module.
  • Experiments based on Sina Weibo dataset validate the performance of the propsed GCN-based model for rumor detection.

2 Main

　　整体框架如下：

　　

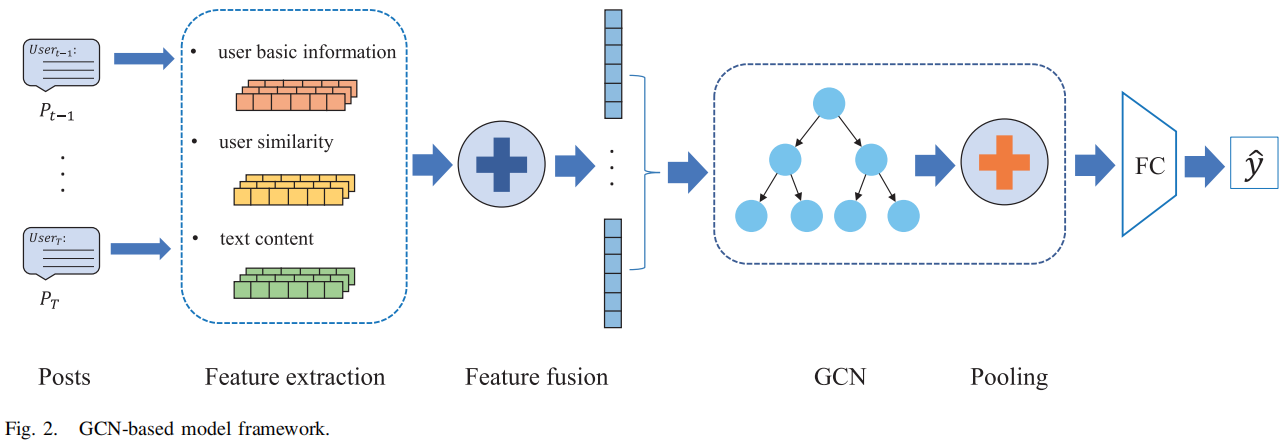
　　主要包括如下四个模块：

1. 1. the feature extraction module
   2. the feature fusion module
   3. the graph convolution module
   4. the pooling module

2.1 Feature Extraction Module

2.1.1 Features of User Basic Information

　　常见的 User basic information：

　　

　　加入这些特征的原因：如 gender 为 女的情况下，是谣言的概率更高。

　　特征预处理：

　　对于 gender 采用 One-hot 向量；

　　对于追随者特征，采用的是 Min-Max normalization ，但是这对于普通用户（如拥有 follower 小的用户）用以造成大部分的数值为 $0$，所以本文采用 $\text{log}$ 处理，如下：

　　　　$x^{*}=\left\{\begin{array}{ll}\frac{\log x-\log x_{\min }}{\log x_{\max }-\log x_{\min }}  & x>0 \\0  & x=0\end{array}\right\} \quad\quad\quad(2)$

　　其中，$x$ 代表归一化前的追随者数量，$x^{*} $ 表示标准化值，$x_{\min }$ 和 $x_{\max }$ 表示中的最小和最大追随者数量。

2.1.2 User Similarity Feature

　　考虑用户相似性，首先构造一个 user-event matrix $M$，其中 User 有 $N_{1}$ 个，event 有 $N_{2}$ 个，所以 $M \in N_{1} \times N_{2}$ 。可以预见的是 $M$ 是一个稀疏矩阵，所以本文采用 SVD 分解：

　　　　$A=U \Sigma V^{T}\quad\quad\quad(3)$

 　　其中 $A$ 为需要分解的矩阵，$U$ 为左奇异值矩阵，$\Sigma$ 为对角矩阵，对角元素为奇异值，$V$ 为右奇异值矩阵。根据奇异值分解在推荐系统中的应用思想，我们可以取前 $N$ 个奇异值，计算 $\Sigma$ 与 $U$ 之间的点积，得到用户的向量表示，从而实现降维的目的。最后，每个用户都将有一个 $N$ 维的向量表示。两个用户向量之间的距离越近，它们共同参与的事件的数量就越多。基于同样的思想，还可以构建 users-users 之间的矩阵，矩阵元素表示两个用户都参与的事件的数量。然后使用相同的方法为用户生成另一组向量特征，并将基于用户-事件矩阵分解为用户相似性特征的向量相结合。

2.1.3 Representation of Text Content

　　使用  $BERT_{base}$ Chinese model 提取文本表示。

2.1.4 Feature Fusion Module

　　直接拼接特征会导致训练不稳定，在 Fig. 3 ，$x \in R^{N \times D_{1}}$ 和 $x^{\prime} \in R^{N \times D_{2}}$ 代表 两个不同的特征向量， $N$ 代表节点的数量，$D_{1}$  和 $D_{2}$ 代表节点的维度。首先将上述特征放入一个两层 的 MLP 模块，然后执行 BN ，

　　　　$\begin{array}{l}\mu \leftarrow \frac{1}{m} \sum\limits_{i=0}^{m} h_{i} \\\sigma^{2} \leftarrow \frac{1}{m} \sum\limits_{i=0}^{m}\left(h_{i}-\mu\right)^{2} \\\hat{h}_{l} \leftarrow \frac{h_{i}-\mu}{\sqrt{\sigma^{2}+\varepsilon}} \\w_{i} \leftarrow \gamma \hat{h}_{i}+\beta\end{array}$

　　其中，$\gamma$ 和 $\beta$ 是可学习参数。

　　最后再执行 concat 。

2.1.5 Graph Convolution Module

　　

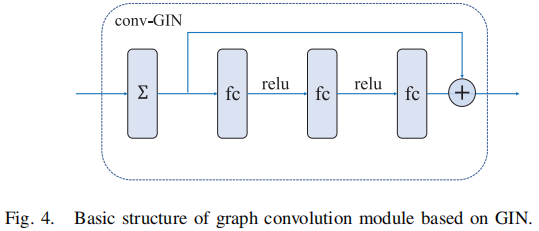
　　GCN 可以编码局部图的结构和节点特征。其正向传播公式如下：

　　　　$H^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}\right)  \quad\quad\quad(8)$

　　 由于 GCN 存在无法识别 multiset 的情况， 所以本文使用 GIN backbone ：

　　　　$w_{v}^{k}=N N^{k}\left(\left(1+\varepsilon^{k}\right) \cdot w_{v}^{k-1}+\sum\limits _{u \in N(v)} w_{u}^{k-1}\right)$

　　最后，将通过 GIN 生成的节点向量放入一个 $3$ 层的全连接网络，并加入残差结构：

　　　　$\widetilde{w}=w+F(w)$

2.1.6 Pooling Module

　　常见的池化操作包括 average pooling 和 maximum pooling，分别如 $\text{Eq.11}$ $\text{Eq.12}$ 所示：

　　　　$\begin{array}{l}h_{G}=\frac{1}{m} \sum\limits _{i=0}^{m} \widetilde{w_{i}} \\h_{G}=\max \left(\widetilde{w_{0}}, \widetilde{w_{1}}, \ldots, \widetilde{w_{m}}\right)\end{array}$

　　平均池化是为了获得图中所有节点的平均向量作为图向量，最大池化是选择此维度中所有节点的最大值作为每个维度的输出。

　　Note：一种新的池化方案，先将节点的表示向量按值降序排列后，选择顶部的 $k$ 个节点，拼接 $k$ 节点向量后，采用一维卷积法进行特征压缩，压缩后的向量为最终的图表示。

　　本文采取的池化过程：将GIN 每层的输入进行concat ，然后使用 Note 中的池化策略。

　　　　$h_{G}=\operatorname{Pooling}\left(\text { Concat }\left(\left\{\widetilde{w_{v}^{k}} \mid k=0,1, \ldots, K\right\}\right) \mid v \in V\right)$

　　最后使用 $h_{G}$ 进行分类：

　　　　$\hat{y}=\operatorname{softmax}\left(F C\left(h_{G}\right)\right)$

3 Experiment

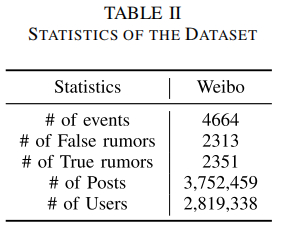
Dataset

　　

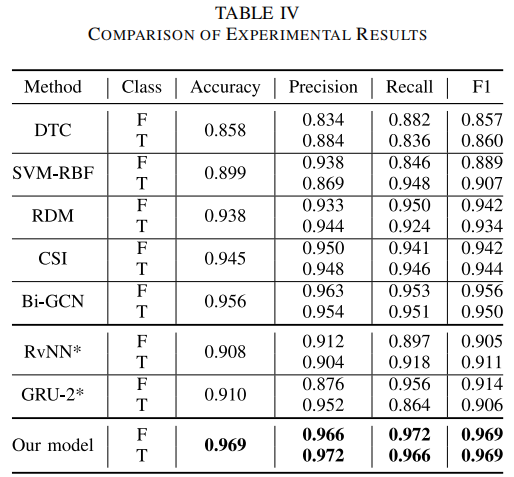
Results