Blair

论文信息

论文标题：Towards Propagation Uncertainty: Edge-enhanced Bayesian Graph Convolutional Networks for Rumor Detection
论文作者：Lingwei Wei, Dou Hu, Wei Zhou, Zhaojuan Yue, Songlin Hu
论文来源：ACL，2021
论文地址：download 
论文代码：download

Abstract

　　由于谣言的产生和传播数据的有限收集，传播结构中不可靠关系造成的不确定性是普遍的和不可避免的。大多数方法都忽视了它，并可能严重限制了对特征的学习。针对这一问题，本文首次尝试探索谣言检测的传播不确定性。具体地说，提出了一种新的Edge-enhanced Bayesian Graph Convolutional Network (EBGCN)来捕获鲁棒的结构特征。该模型采用贝叶斯方法，自适应地重新考虑了潜在关系的可靠性。此外，设计了一个新的边一致性训练框架，通过加强关系上的一致性来优化模型。在三个公共基准数据集上的实验表明，该模型在谣言检测和早期谣言检测任务上都比基线方法具有更好的性能。

1 Introduction

　　目前大多数工作将推文之间的关系视为消息传递的可靠边。如 Figure 1 所示，不准确关系的存在给传播结构带来了不确定性。忽略不可靠关系会导致多层消息传递导致严重的错误积累，限制对有效特征的学习。

　　

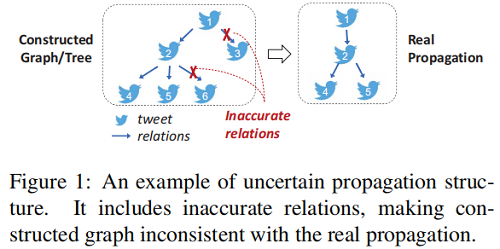
　　本文认为，传播结构中固有的不确定性在两个方面是不可避免的：

　　i) 由于虚假的支持性推文存在；

　　ii) 传播关系的主观性和稀疏性；

　　本文贡献：

• • 提出了一种新的边增强贝叶斯图卷积网络（EBGCN）来以概率的方式处理不确定性；
  • 设计了一个新的边一致性训练框架来优化具有无标记潜在关系的模型；

2 Problem Statement

　　

3 The Proposed Model

　　整体框架如下：

3.1 Overview

　　主要流程：

• • 首先，谣言传播树的传播结构表示为具有两个相反方向的有向图【 a top-down propagation graph and a bottom-up dispersion graph】。

  • 其次，文本内容由文本嵌入层进行嵌入。

• • 然后，通过节点更新模块【node update module】和边推理模块【edge inference module】这两个主要组件迭代捕获丰富的结构特征。

  • 最后，我们聚合节点嵌入来生成图嵌入并输出声明的标签。

　　对于训练，在通过失去无标记潜在关系的贝叶斯上加入无监督一致性训练。因此，通过最小化无监督损失和有监督损失的加权和来优化模型。

3.2 Edge-enhanced Bayesian Graph Convolutional Networks

3.2.1 Graph Construction and Text Embedding

　　对于每个 $c^{i}$，top-down propagation graph 和 bottom-up dispersion graph 表示为 $G_{i}^{T D}$  和  $G_{i}^{B U}$ ，对应的邻接矩阵表示为 $\mathbf{A}_{i}^{T D}=\mathbf{A}_{i}$ 和 $\mathbf{A}_{i}^{B U}=\mathbf{A}_{i}^{\top}$。

　　对于每个 claim $c$，其特征矩阵采用 Top-5000 words 并用 TF-IDF 初始化，定义为 $\mathbf{X}=\left[\mathbf{x}_{0}, \mathbf{x}_{1}, \ldots, \mathbf{x}_{n-1}\right] \in   \mathbb{R}^{n \times d_{0}}$，$\mathbf{x}_{0} \in \mathbb{R}^{d_{0}}$ 代表源推文的特征向量，对于 propagation graph 和 dispersion graph ，对应的特征矩阵为 $\mathbf{X}^{T D}=\mathbf{X}^{B U}=\mathbf{X}$。

3.2.2 Node Update

　　GCN 公式：

　　　　$\mathbf{H}^{(l)}=\sigma\left(\hat{\mathbf{A}}^{(l-1)} \mathbf{H}^{(l-1)} \mathbf{W}^{(l)}+\mathbf{b}^{(l)}\right)   \quad\quad\quad(1)$

　　具体来说，我们通过基于上一层的节点表示计算一个变换 $f_{e}\left(\cdot ; \theta_{t}\right)$ 来调整两个节点之间的权重。然后，邻接矩阵将被更新，即：

　　　　$\begin{aligned}\mathbf{g}_{t}^{(l)} &=f_{e}\left(\left\|\mathbf{h}_{i}^{(l-1)}-\mathbf{h}_{j}^{(l-1)}\right\| ; \theta_{t}\right) \\\mathbf{A}^{(l)} &=\sum_{t=1}^{T} \sigma\left(\mathbf{W}_{t}^{(l)} \mathbf{g}_{t}^{(l)}+\mathbf{b}_{t}^{(l)}\right) \cdot \mathbf{A}^{(l-1)}\end{aligned} \quad\quad\quad(2)$

　　在实践中，$f_{e}\left(\cdot ; \theta_{t}\right)$ 由一个卷积层和一个激活函数组成。$\sigma(\cdot)$ 是一个 sigmoid 函数。$\mathbf{W}_{t}^{(l)}$ 和 $\mathbf{W}_{t}^{(l)}$ 是可学习的参数。

　　本文在 $G^{T D}$ 和 $G^{B U}$ 两个图中执行边缘推理层的共享参数。经过两层变换叠加后，模型可以有效地累积由潜在关系驱动的邻居特征的归一化和，记为 $\mathbf{H}^{T D}$ 和$\mathbf{H}^{B U}$。

3.2.4 Classification

　　给定 propagation graph $\mathbf{H}^{T D}$ 中的节点表示和 dispersion graph $\mathbf{H}^{B U}$ 中的节点表示，该图的表示可以计算为：

　　　　$\begin{array}{l}\mathbf{C}^{T D}=\text { meanpooling }\left(\mathbf{H}^{T D}\right) \\\mathbf{C}^{B U}=\text { meanpooling }\left(\mathbf{H}^{B U}\right)\end{array}  \quad\quad\quad(3)$

　　其中，$meanpooling (\cdot)$ 指的是平均池聚合函数。基于两种不同的图表示的连接，所有类的标签概率可以由一个全连接层和一个 softmax 函数来定义，即：

　　　　$\hat{\mathbf{y}}=\operatorname{softmax}\left(\mathbf{W}_{c}\left[\mathbf{C}^{T D} ; \mathbf{C}^{B U}\right]+\mathbf{b}_{c}\right)\quad\quad\quad(4)$

3.3 Edge-wise Consistency Training Framework

For the supervised learning loss  $\mathcal{L}_{c}$

　　监督损失 $\mathcal{L}_{c}$ 采用交叉熵损失：

　　　　$\mathcal{L}_{c}=-\sum_{i}^{|\mathcal{Y}|} \mathbf{y}^{i} \log \hat{\mathbf{y}}^{i}$

　　其中，$C=\left\{c_{1}, c_{2}, \ldots, c_{m}\right\}$ 代表着 ground truth distributions，$\mathbf{y}^{i}$ 是表示第 $i$ 个 claim 样本的地面真实标签分布的向量。

For the unsupervised learning loss $\mathcal{L}_{e}$

　　对于无监督学习损失 $\mathcal{L}_{e}$，我们将分类权重 $p(\varphi)$ 的后验分布摊销为 $q(\varphi)$，以便在测试阶段进行快速预测，并通过最小化潜在关系的平均预期损失来学习参数，即 $\varphi^{*}=\arg \min _{\varphi} \mathcal{L}_{e}$，其中

　　　　$\begin{aligned}\mathcal{L}_{e} &=\mathbb{E}\left[D_{K L}\left(p\left(\hat{\mathbf{r}}^{(l)} \mid \mathbf{H}^{(l-1)}, G\right) \| q_{\varphi}\left(\hat{\mathbf{r}}^{(l)} \mid \mathbf{H}^{(l-1)}, G\right)\right)\right] \\\varphi^{*} &=\arg \max _{\varphi} \mathbb{E}\left[\log \int p\left(\hat{\mathbf{r}}^{(l)} \mid \mathbf{H}^{(l-1)}, \varphi\right) q_{\varphi}\left(\varphi \mid \mathbf{H}^{(l-1)}, G\right) d \varphi\right]\end{aligned}\quad\quad\quad(6)$

　　其中，$\hat{\mathbf{r}}$ 为潜在关系的预测分布。为了保证可能性，我们独立地建模每个潜在关系 $r_{t}$，$t \in [1, T]$ 的先验分布。对于每个关系，我们定义了每个潜在关系 $q_{\varphi}\left(\varphi \mid \mathbf{H}^{(l-1)}, G ; \Theta\right)$ 的一个分解高斯分布，均值 $\mu_{t}$ 和方差 $\delta_{t}^{2}$ 由变换层设置。

　　　　$\begin{array}{l}\left.q_{\varphi}\left(\varphi \mid \mathbf{H}^{(l-1)}, G ; \Theta\right)\right) =\prod_{t=1}^{T} q_{\varphi}\left(\varphi_{t} \mid\left\{\mathbf{g}_{t}^{(l)}\right\}_{t=1}^{T}\right)=\prod_{t=1}^{T} \mathcal{N}\left(\mu_{t}, \delta_{t}^{2}\right) \\\mu_{t}=f_{\mu}\left(\left\{\mathbf{g}_{t}^{(l)}\right\}_{t=1}^{T} ; \theta_{\mu}\right), \quad\quad \delta_{t}^{2}=f_{\delta}\left(\left\{\mathbf{g}_{t}^{(l)}\right\}_{t=1}^{T} ; \theta_{\delta}\right)\end{array}  \quad\quad\quad(7)$

　　其中，$f_{\mu}\left(\cdot ; \theta_{\mu}\right)$ 和 $f_{\delta}\left(\cdot ; \theta_{\mu}\right)$代表分别计算输入向量的均值和方差，分别由 $\theta_{\mu}$ 和 $\theta_{\delta}$ 参数化。

　　此外，在参数化原型向量的后验分布时，我们还考虑了潜在关系的可能性。基于节点嵌入的第 $l$ 层潜在关系的可能性可以自适应地计算：

　　　　$\begin{aligned}p\left(\hat{\mathbf{r}}^{(l)} \mid \mathbf{H}^{(l-1)}, \varphi\right) &=\prod\limits_{t=1}^{T} p\left(\hat{\mathbf{r}}_{t}^{(l)} \mid \mathbf{H}^{(l-1)}, \varphi_{t}\right) \\p\left(\hat{\mathbf{r}}_{t}^{(l)} \mid \mathbf{H}^{(l-1)}, \varphi_{t}\right) &=\frac{\exp \left(\mathbf{W}_{t} \mathbf{g}_{t}^{(l)}+\mathbf{b}_{t}\right)}{\sum\limits_{t=1}^{T} \exp \left(\mathbf{W}_{t} \mathbf{g}_{t}^{(l)}+\mathbf{b}_{t}\right)}\end{aligned} \quad\quad\quad(8)$

　　这样，就可以根据观察到的图自适应地调整边的权值，从而有效地传递信息，学习更多的鉴别特征来检测谣言。综上所述，在训练中，我们通过最小化标记索赔 $\mathcal{L}_{c}$ 的交叉熵损失，并通过未标记潜在关系的反向支撑损失 $\mathcal{L}_{e}$，即：

　　　　$\Theta^{*}=\arg \min _{\Theta} \gamma \mathcal{L}_{c}+(1-\gamma) \mathcal{L}_{e} \quad\quad\quad(9)$

4 Experiment

Datasets

　　

Results

　　

5 Conclusion

　　本文从概率的角度研究了谣言检测中传播结构中的不确定性。具体地说，我们提出了边缘增强的贝叶斯图卷积网络（EBGCN），通过自适应地调整不可靠关系的权值，用贝叶斯方法来处理不确定性。此外，我们还设计了一个结合无监督关系学习的边缘一致性训练框架，以加强潜在关系的一致性。在三个常见的基准数据集上进行的大量实验已经证明了在传播结构中对不确定性进行建模的有效性。EBGCN在谣言检测和早期谣言检测任务上都显著优于基线任务。