论文解读（ASAP）《ASAP: Adaptive Structure Aware Pooling for Learning Hierarchical Graph Representations》

论文信息

论文标题：ASAP: Adaptive Structure Aware Pooling for Learning Hierarchical Graph Representations
论文作者：Ekagra Ranjan, Soumya Sanyal, Partha Pratim Talukdar
论文来源：2020,AAAI
论文地址：download
论文代码：download

1 Introduction

　　TopK Pooling 基于可学习的投影向量对节点进行评分，并对部分高分数节点进行采样。它避免了节点聚合和计算软分配矩阵，以保持图操作的稀疏性。

　　　　$\begin{array}{l}\mathbf{y} &=\frac{\mathbf{X} \mathbf{p}}{\|\mathbf{p}\|} \\\mathbf{i} &=\operatorname{top}_{k}(\mathbf{y}) \\\mathbf{X}^{\prime} &=(\mathbf{X} \odot \tanh (\mathbf{y}))_{\mathbf{i}} \\\mathbf{A}^{\prime} &=\mathbf{A}_{\mathbf{i}, \mathbf{i}}\end{array}$

　　SAGPool 对 TopK 进行了改进，在对节点进行评分时使用 GNN 来考虑图结构。

　　　　$\begin{array}{l}\mathbf{y} &=\mathbf{G N N}(\mathbf{X}, \mathbf{A}) \\\mathbf{i} &=\operatorname{top}_{k}(\mathbf{y}) \\\mathbf{X}^{\prime} &=(\mathbf{X} \odot \tanh (\mathbf{y}))_{\mathbf{i}} \\\mathbf{A}^{\prime} &=\mathbf{A}_{\mathbf{i}, \mathbf{i}}\end{array}$

　　由于 TopK 和 SAGPool 不聚合节点，也不计算软边权值，因此它们无法有效地保存节点和边缘信息。

　　为了解决这些限制，本文提出了 ASAP，它具有 hierarchical pooling 的所有理想特性，而不影响图操作中的稀疏性。

　　ASAP 对比经典方法：

　　

2 ASAP: Proposed Method

　　整体框架如下：

　　

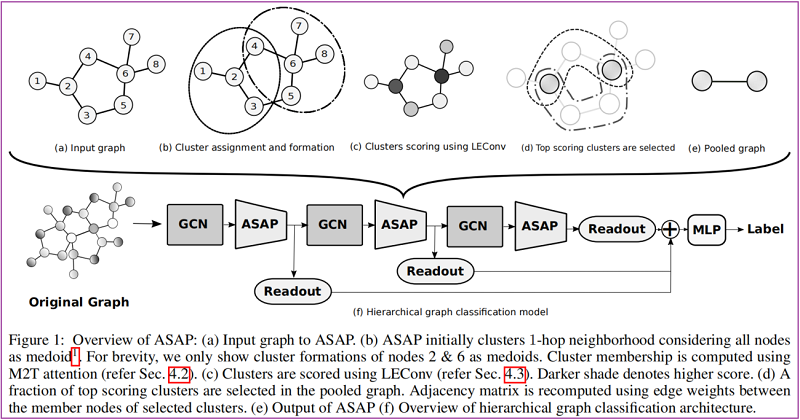
　　主要步骤：

• • Fig.1(b)：ASAP首先为一个给定的输入图考虑所有可能的具有固定接受域的局部簇，然后使用注意机制计算节点的集群隶属度；
  • Fig.1(c)：使用GNN对这些簇进行评分；
  • Fig.1(d)：选择部分得分最高的簇作为合并图中的节点，并在相邻簇之间计算新的边权值；

2.1 Cluster Assignment

　　首先，将图中的每个节点 $v_{i}$ 视为一个簇 $c_{h}\left(v_{i}\right)$ 的 medoid，这样每个簇只能表示在固定的 $h$ 跳半径内的局部邻居 $\mathcal{N}$，即 $c_{h}\left(v_{i}\right)=\mathcal{N}_{h}\left(v_{i}\right)$。有效地意味着 $R F^{\text {node }}=h$，这有助于集群有效地捕获图子结构中存在的信息。设 $x_{i}^{c}$ 是以 $v_{i}$ 为中心的集群 $c_{h}\left(v_{i}\right)$ 的特征表示。将 $G^{c}\left(\mathcal{V}, \mathcal{E}, X^{c}\right)$ 定义为以  $X^{c} \in \mathbb{R}^{N \times d}$ 为特征矩阵，$A^{c}=A$ 为邻接矩阵的图。定义聚类分配矩阵 $S \in \mathbb{R}^{N \times N}$，其中 $S_{i, j}$ 代表着 $v_{i} \in \mathcal{V}$ 在簇 $c_{h}\left(v_{j}\right)$ 中的关系。通过使用这种局部聚类，可以保持聚类分配矩阵 $S$ 的稀疏性，类似于原始图邻接矩阵 $A$，即 $S$ 和 $A$ 的空间复杂度都为 $\mathcal{O}(|\mathcal{E}|)$。

2.2 Cluster Formation using Master2Token

　　给定一个聚类 $c_{h}\left(v_{i}\right)$，通过一个自注意机制来学习聚类分配矩阵 $S$。这里的任务是通过关注集群 $c_{h}\left(v_{i}\right)$ 中的相关节点来学习集群 $c_{h}\left(v_{i}\right)$ 的整体表示。本文提出了一种新的自注意机制变体，称为 Master2Token(M2T)。我们在后面的章节中进一步激发了对M2T框架的需要。

　　在 M2T 框架中，首先创建一个 master query $m_{i} \in \mathbb{R}^{d}$，它代表了一个集群中的所有节点：

　　　　$\left.m_{i}=f_{m}\left(x_{j}^{\prime} \mid v_{j} \in c_{h}\left(v_{i}\right)\right\}\right)\quad\quad\quad(4)$

　　$f_{m}$ 是一个主函数，它结合和转换 $v_{j} \in c_{h}\left(v_{i}\right)$ 的特征表示来找到 $m_{i}$。在这项工作中，我们实验了最大主函数定义为：

　　　　$m_{i}=\max _{v_{j} \in c_{h}\left(v_{i}\right)}\left(x_{j}^{\prime}\right)$

　　这个 master query $m_{i}$ 关注所有组成节点 $v_{j} \in c_{h}\left(v_{i}\right)$：

　　　　$\alpha_{i, j}=\operatorname{softmax}\left(\vec{w}^{T} \sigma\left(W m_{i} \| x_{j}^{\prime}\right)\right)$

　　$\alpha_{i, j}$ 表示集群 $c_{h}\left(v_{i}\right)$ 中节点 $v_{j}$ 的成员资格强度。因此，我们使用这个分数来定义上面讨论的集群分配矩阵 $S_{i, j}=\alpha_{i, j}$ 。$c_{h}\left(v_{i}\right)$ 的集群表示 $x_{i}^{c}$ 的计算方法如下：

　　　　$x_{i}^{c}=\sum\limits _{j=1}^{\left|c_{h}\left(v_{i}\right)\right|} \alpha_{i, j} x_{j}$

2.3 Cluster Selection using LEConv

　　与 TopK 类似，我们使用适应度函数 $f_{\phi}$ 计算图 $G^{c}$ 中每个聚类的群集适应度得分 $\phi_{i}$ 对聚类进行抽样。对于一个给定的池化比率 $k \in(0,1]$，选择 top $\lceil k N\rceil$ 的簇并包含在合并图 $G^{p}$ 中。为了计算适应度分数，我们引入了Local Extrema Convolution(LEConv)，这是一种可以捕获局部极值信息的图卷积方法。

　　LEConv 用于计算 $\phi$ 如下：

　　　　$\phi_{i}=\sigma\left(x_{i}^{c} W_{1}+\sum\limits _{j \in \mathcal{N}(i)} A_{i, j}^{c}\left(x_{i}^{c} W_{2}-x_{j}^{c} W_{3}\right)\right)$

 　　其中，$\mathcal{N}(i)$ 表示 $G^{c}$ 中第 $i$ 个节点的邻域。$W_{1}$、$W_{2}$、$W_{3}$ 是可学习的参数 和 $\sigma(.)$ 是一些激活函数。将适应度向量 $\Phi=\left[\phi_{1}, \phi_{2}, \ldots, \phi_{N}\right]^{T}$ 乘以聚类特征矩阵 $X^{c}$，使 $f_{\phi}$ 可学习，即：

　　　　$\hat{X}^{c}=\Phi \odot X^{c}$

　　其中 $\odot$ 为 broadcasted hadamard product ，函数 $\mathrm{TOP}_{k} (.)$ 对适应度评分进行排序，并给出 $G^{c}$ 中 $top \lceil k N\rceil$ 选择的聚类指标 $\hat{i}$ 如下：

　　　　$\hat{i}=\operatorname{TOP}_{k}\left(\hat{X}^{c},\lceil k N\rceil\right) $

　　pooled graph $G^{p}$ 是通过选择这些 $top \lceil k N\rceil$ 个簇来形成的。修剪后的簇分配矩阵 $\hat{S} \in \mathbb{R}^{N \times\lceil k N\rceil}$ 和节点特征矩阵如下：

　　　　$\hat{S}=S(:, \hat{i}), \quad X^{p}=\hat{X}^{c}(\hat{i},:)$

　　其中，$\hat{i}$ 用于索引切片。

2.4 Maintaining Graph Connectivity

　　一旦簇被采样成功，我们使用 $\hat{A}^{c}$ 和 $\hat{S}$ 去生成 $G^{p}$ 的 新的邻接矩阵 $A^{p}$：

　　　　$A^{p}=\hat{S}^{T} \hat{A}^{c} \hat{S}$

　　其中，$\hat{A}^{c}=A^{c}+I$ ，$A_{i, j}^{p}=   \sum_{k, l} \hat{S}_{k, i} \hat{A}_{k, l}^{c} \hat{S}_{l, j}$。

3 Experiments

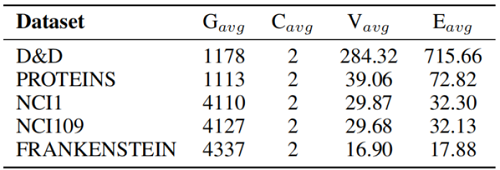
数据集

　　

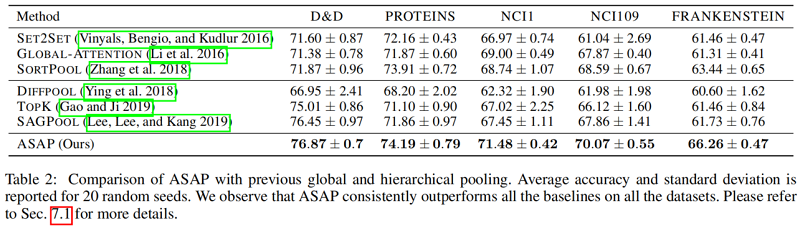
图分类

　　

附录

ASAP algorithm：

　　

MASTER2TOKEN algorithm

　　

 

===============