论文解读（soft-mask GNN）《Soft-mask: Adaptive Substructure Extractions for Graph Neural Networks》

论文信息

论文标题：Soft-mask: Adaptive Substructure Extractions for Graph Neural Networks
论文作者：Mingqi Yang, Yanming Shen, Heng Qi, Baocai Yin
论文来源：2021, WWW
论文地址：download 
论文代码：download 

1 Abstract

　　GNN 应该能够有效地提取与任务相关的结构，并且对无关的部分保持不变。

　　本文提出的解决方法：从原始图的子图序列中学习图的表示，以更好地捕获与任务相关的子结构或层次结构，并跳过噪声部分。

　　该论文建议看看代码，论文写的令人疑惑......(代码简单)

2 Introduction

 　　消息传递机制的回顾：

　　　　$\begin{aligned}h_{\mathcal{N}(i)}^{(l+1)} &=\text { aggregate }\left(\left\{h_{j}^{l}, \forall j \in \mathcal{N}(i)\right\}\right) \\h_{i}^{(l+1)} &=\sigma\left(W \cdot \operatorname{concat}\left(h_{i}^{l}, h_{\mathcal{N}(i)}^{+1}\right)\right) \\h_{i}^{(l+1)} &=\operatorname{norm}\left(h_{i}^{(l+1)}\right)\end{aligned}$

　　

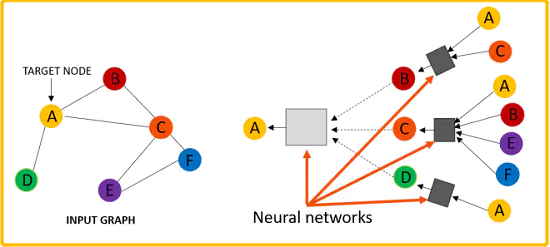
　　消息传递机制的问题：

• • 所有节点在更新表示的时候，共享着一样的权重；
  • 与任务相关的结构信息很可能与不相关（或噪声）部分混合，使得下游处理无法区分，特别是对于深度模型[4,17,22]中更高层捕获的长期依赖；

　　直观的解决方法是：区分不同的图拓扑结构，希望有用的结构信息将被保留并传递到更高的层次进行进一步处理。​例如：GIN [32]​、[5, 18, 19]​。

　　对于具有层次结构的图，GNNs 应该以分层的方式对它们进行编码，一个高度为 $2$的层次图的简单例子，如 Figure 1 (a) 所示：

　　

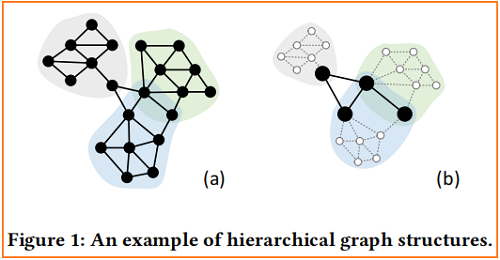
　　Figure 1(b) 表明，在本图中，节点可以分为两组：

• • Leaf node. Nodes only have connections within each part such as white nodes in Figure 1(b)；
  • Root node. Nodes have connections with other parts or shared with other parts such as black nodes in Figure 1(b)；

　　底层使用 leaf node 进行子图学习，高层使用  Root node 进行层次表示学习。

　　根据以上分析，从一组子图序列中学习图表示实际上统一了子图表示学习和层次表示学习。要实现这一目标，主要面临两个挑战：

• • 如何在保持可微性的同时有效地表示每一层中的任何随机子图？
  • 如何决定由模型学习到的子图的序列？

 　　两类现有工作：

• • GAM [16] 通过表示一个包含从原始图中采样的固定长度的节点序列的图来提取所需的子结构；
  • Top-k graph pooling [7,14,15] 对每个节点的重要性进行评分，并逐层删除低评分节点和相关边；

　　这些策略可以动态地关注信息部分，使神经网络在处理噪声图时更加鲁棒。然而，GAM 要求采样的节点序列具有固定的长度，而 top-k 池需要一个固定的下降比，这限制可能是用任意尺度表示所需的子图的障碍。

　　本文提出的 soft-mask GNN，它通过控制节点掩码来提取任何大小的子图。然后将寻找所需子图的问题转化为寻找适当的掩模分配。

2 Graph Neural Networks

　　在形式上，GNN 的第 $k$ 层为：

　　　　$\mathbf{h}_{v}^{(k)}=\operatorname{Update}\left(\mathbf{h}_{v}^{(k-1)}, \operatorname{Aggregate}\left(\left\{\left\{\mathbf{h}_{u}^{(k-1)} \mid u \in \mathcal{N}(v)\right\}\right\}\right)\right)  \quad\quad\quad(1)$

　　最后一层的节点嵌入矩阵可以直接用于节点分类，而对于图分类需要进一步做 Readout 处理：

　　　　$\mathbf{h}_{G}=\operatorname{Readout}\left(\left\{\left\{\mathbf{h}_{v}^{(K)} \mid v \in V_{G}\right\}\right\}\right)\quad\quad\quad(2)$

　　最后将 $\mathbf{h}_{G}$ 传递给一个分类器进行图分类。

　　在 $\text{Eq.1}$ 中，$Aggregate(.)$ 用于聚合邻居的表示以生成当前节点表示，在 $\text{Eq.2}$ 中 $Readout(.)$，用于聚合所有节点表示，以生成整个图表示。为了使 GNN 对图的同构不变，$Aggregate(.)$ 和 $Readout(.)$ 应该是排列不变的。同时，$\text{Eq.1}$ 和$\text{Eq.2}$ 应该是可微的，以使网络可以通过反向传播进行训练。

3 Soft-mask GNN

　　在本节中，首先介绍SMG层，并解释如何通过控制掩码分配来提取所需的子图。然后，展示多层 SMG 如何分别学习具有相应子图序列的子图的表示和层次表示。还提出了一种计算掩模分配的方法，它可以通过反向传播自动提取子结构或层次结构。最后，将SMG推广到多通道场景中。

3.1 Sparse Aggregation and Subgraph Representation Learning

　　GNN 操作被看作是一种平滑操作 [4,17,22]，其中每个节点与其相邻节点交换特征信息。这种方案不会明确地跳过不相关的部分。相反，我们的 SMG 层提取的子结构如下：

　　　　$\mathbf{h}_{v}^{(k)}=\operatorname{ReLU}\left(\mathbf{W}_{1}^{(k)} m_{v}^{(k)}\left[\mathbf{h}_{v}^{(k-1)} \| \sum\limits _{u \in \mathcal{N}(v)} m_{u}^{(k)} \mathbf{h}_{u}^{(k-1)}\right]\right) \quad\quad\quad(2)$

　　其中 $m_{v}^{(k)} \in[0,1]$ 为节点 $v$ 在第 $k$ 层的 soft-mask，$||$ 表示连接操作，$\mathbf{W}_{1}^{(k)} \in \mathrm{R}^{d \times d}$ 为可训练矩阵，其中 $d$ 为节点表示的维数。$m_{v}^{(k)}$ 的计算将在第 3.3 节中介绍。SMG 图层应满足以下约束条件：

• 线性变换 $\mathrm{W}_{1}^{(k)}$ 不包括常数部分（即 bias）；
• 激活函数(ReLU)满足 $\sigma(0)=0$；
• 聚合运算符(SUM)为 zero invariant；

　　Zero invariant. The aggregation function  $f:\left\{\left\{\mathbb{R}^{m}\right\}\right\} \rightarrow \mathbb{R}^{n}$  is zero invariant if and only if

　　　　$f(\mathcal{S})=\left\{\begin{array}{ll}0 & \mathcal{S}=\emptyset \\f(\mathcal{S} /\{\mathbf{0}\}) & \text { otherwise }\end{array}\right.$

　　其中，$\mathcal{S}$ 是一个向量的多集。注意，SUM算符是  zero invariant，而 MEAN 不是。

　　有了上述限制，

• • 对于中心节点 $v$ ，设置  $m_{v}^{(k)}=0$ ，有 $\mathbf{h}_{v}^{(k)}=0$ ；
  • 对于 $v$ 的邻域 $u \in \mathcal{N}(v)$，有 $\mathbf{h}_{u}^{(k)}=\operatorname{ReLU}\left(\mathbf{W}_{1}^{(k)} m_{u}^{(k)}\left[\mathbf{h}_{u}^{(k-1)} \| \sum_{u^{\prime} \in \mathcal{N}(u) /\{v\}} m_{u^{\prime}}^{(k)} \mathbf{h}_{u^{\prime}}^{(k-1)}\right]\right)$；

　　即节点 $v$ 对其邻居是不可访问的。因此，对于任何 $G$ 的子图 $G_{S}$，一层 SMG 和一个 zero invariant Readout 函数可以表示子图 $G_{S}$。并且可以跳过其他部分，通过控制 mask 分配：

　　　　$ \begin{array}{l}&\mathbf{h}_{G}|_{    m_{v}^{(1)}=1, v \in V_{G_{S}} ; m_{v}^{(1)}=0, v \in V_{G} / V_{G_{S}}    }\\&=\sum\limits_{v \in V_{G_{S}}} \mathbf{h}_{v}^{(1)}+\sum\limits_{v \in V_{G} / V_{G_{S}}} \mathbf{h}_{v}^{(1)} \\&=\sum\limits_{v \in V_{G_{S}}} \operatorname{ReLU}\left(\mathbf{W}_{1}^{(1)}\left[\mathbf{x}_{v} \| \sum\limits_{u \in \mathcal{N}_{G_{S}}(v)} \mathbf{x}_{u}\right]\right)+\mathbf{0} \\&=\left.\mathbf{h}_{G_{S}}\right|_{m_{v}^{(1)}=1, v \in V_{G_{S}}} .\end{array}$

　　Note：根据上述公式 ，知要求子图 $G_{S}$ 的表示，设置 $m_{u}=1$ 。

　　它消除了一般 GNNs 的限制，即在所有节点上进行聚合，因此我们称之为 sparse aggregation。所选的子图包括具有 $mask=1$ 和相关边的所有节点。

在多层SMG中

　　不管在多层 SMG 或者单层SMG 中均满足：为学习同一个子图 $G_{S}$ 的子图表示，设置  $m_{v}^{(k)}=1$  for all  $v \in V_{G_{S}}$  、$m_{u}^{(k)}=0$  for all  $u \in   V_{G} / V_{G_{S}}$  in all layers. 

　　不同的子图所对应的 mask 序列是不一样的。

　　然而，并不是所有分配在不同层中的节点上的掩码都对最终的表示有影响，而且某些层中的掩码可以取任意值。由于不同的掩码导致不同的子图序列，这意味着所需的子图表示可能对应于不同的子图序列。

　　在多层 SMG 中，具有 $m_{u}^{(k)}=0$ 的节点实际上不会被删除。以下各层中的 GNN 操作也会涉及到它们。为了表示子图 $G_{S}$，一个基本思想是通过为 $v \in V_{G_{S}}$ 分配 $m_{v}^{(k)}=1$，并为$u \in   V_{G} / V_{G_{S}}$ 分配 $m_{u}^{(k)}=0$ ，来限制在同一子图 $G_{S}$ 上学习。

　　这对应于一个所有子图都相同的特定子图的序列。然而，并不是所有分配在不同层中的节点上的掩码都对最终的表示有影响，而且某些层中的掩码可以取任意值。由于不同的掩码导致不同的子图序列，这意味着所需的子图表示可能对应于不同的子图序列。为了解释这个问题，我们使用 $\mathbf{H}_{G}^{(k)}=\left\{\left\{\mathbf{h}_{v}^{(k)} \mid v \in V_{G}\right\}\right\}=\mathrm{SMG}_{k}\left(\mathbf{X}_{G}, \mathbf{A}_{G}, \mathbf{M}\right)$ 去代表表示由 $k$ 层 SMG 学习到的节点表示集，其中输入的 $\mathbf{M} \in[0,1]^{k \times n}$ 是在所有 $k$ 层上预先分配的掩码，使用 $\mathbf{M}_{k, v}=m_{v}^{(k)}$ 。$M$ 定义了一个长度为 $k$ 的子图序列。$\hat{\mathbf{H}}_{G}^{(k)}=\left\{\left\{\hat{\mathbf{h}}_{v}^{(k)} \mid v \in V_{G}\right\}\right\}=\operatorname{SMG}_{k}\left(\mathbf{X}_{G}, \mathbf{A}_{G}, 1\right) $ 是由 k-layer SMG与$\mathbf{M}=1^{k \times n}$ 学习到的节点表示集，以及相应的 $\hat{\mathbf{h}}_{v}^{(k)}=\operatorname{ReLU}\left(\mathbf{W}_{1}^{(k)}\left[\hat{\mathbf{h}}_{v}^{(k-1)} \| \sum_{u \in \mathcal{N}(v)} \hat{\mathbf{h}}_{u}^{(k-1)}\right]\right)$ 。

　　Lemma 3.1. For any subgraph  $G_{S}$  of  $G$ , Let  $\mathbf{H}_{G}^{(K)}=\left\{\left\{\mathbf{h}_{v}^{(k)} \mid v \in\right.\right.   \left.\left.V_{G}\right\}\right\}$  and  $\hat{\mathbf{H}}_{G_{S}}^{(K)}=\left\{\left\{\hat{\mathbf{h}}_{v}^{(k)} \mid v \in V_{G_{S}}\right\}\right\}$ . Then we have  $\mathbf{h}_{v}^{(K)}=\hat{\mathbf{h}}_{v}^{(K)}$  for any  $v \in V_{G_{S}}$ , if the following condition holds,

　　　　$\mathbf{M}_{k, v}=m_{v}^{(k)}=\left\{\begin{array}{ll}0 & \{v\} \subseteq V_{G} / V_{G_{S}} \\& \wedge \mathcal{N}_{G}(v) \cap V_{G_{S}} \neq \emptyset \\& \wedge k \% 2=1 \\1 & \{v\} \subseteq V_{G_{S}} \wedge\{k\} \subseteq[K]\end{array}\right.$

　　

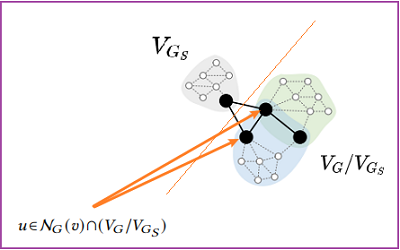
　　证明：

　　

　　$\mathbf{h}_{u}^{(k-1)}=0$ 由于 $\mathbf{h}_{u}^{(k)}=\operatorname{ReLU}\left(\mathbf{W}_{1}^{(k)} m_{u}^{(k)}\left[\mathbf{h}_{u}^{(k-1)} \| \sum_{u^{\prime} \in \mathcal{N}(u) /\{v\}} m_{u^{\prime}}^{(k)} \mathbf{h}_{u^{\prime}}^{(k-1)}\right]\right)$

　　Theorem 3.2. Let  $\mathbf{h}_{G}=S U M\left(\mathbf{H}_{G}^{(K)}\right)$  and  $\hat{\mathbf{h}}_{G_{S}}=S U M\left(\hat{\mathbf{H}}_{G_{S}}^{(K)}\right)$ , where  $G_{S}$  can be any subgraph of  $G$ . Then there exist assignments of  $\mathbf{M}$  such that  $\mathbf{h}_{G}=\hat{\mathbf{h}}_{G_{S}}$ .

　　证明：

　　

　　Lemma 3.1 和 Theorem 3.2 表明，子图的表示对应于一组 $M$，所以可以将寻找子图的问题转化为寻找合适的 $M$。

3.2 Hierarchical Representation Learning

　　如 Figure 1(a)所示的层次图由每个单独的部分及其相互作用组成。同时，每个部分由几个较小部分的交互组成，使图结构识别递归。为了捕获层次结构，神经网络应该首先单独编码每个局部部分，然后编码它们的相互作用。从节点的角度来看，首先聚合叶节点，然后考虑根节点。这对应于堆叠多个SMGs，其中每个 $\mathrm{SMG}_{k_{i}}$ 学习子图 $G_{S_{i}}$ 的节点表示，输入节点特征是由之前的 $\mathrm{GNN}_{k_{i-1}}$ 学习到的节点表示。在第 $i$ 层的 $\mathrm{GNN}_{k_{i}}$ 中，$\mathbf{H}_{G}^{\star}=\mathrm{SMG}_{k_{i}}\left(\mathrm{H}_{G}^{\star-k_{i}}, \mathbf{A}_{G}, \mathbf{M}_{G_{S_{i}}}\right)$，其中 $\mathbf{M}_{G_{S_{i}}}$ 是 Lemma 3.1 对应于 $G_{S_{i}}$ 的赋值，$k_{i}$ 是 $\mathrm{SMG}_{k_{i}}$ 的层数。在第一步中，$\mathbf{H}_{G}^{0}=\mathbf{X}_{G}$ 。

　　我们用 Figure 1 中的层次图示例来解释这个过程。其层次结构的特点是由三个独立的部分及其相互作用组成。我们使用 $2$ 层的 SMGs 学习这个图表，如  Figure 2 所示。根据 Lemma 3.1 的观察，$\mathrm{SMG}_{k_{1}}$ 学习到的表示对应于只涉及子图1的叶节点，导致学习到的节点表示被限制在相应的部分内。此外，$\mathrm{SMG}_{k_{2}}$ 学习到的表示对应于子图2中的由根节点（黑色）和叶节点（灰色）组成的，它们捕获每个部分以及它们的相互作用。一致地，要扩展到高度大于 $2$ 的层次图，需要在特定子图上学习的每个叠加更多的 SMGs 。低水平的不同部分的相互作用被较低的  SMGs捕获，而高水平的相互作用被较高的 SMGs 捕获。

　　

　　我们已经展示了如何通过将多个 SMGs 叠加到每个 SMGs 对应于一个子图中来捕获层次结构，如 Lemma 3.1中所分析的那样。这是假设我们是了解图的层次结构的。然而，层次结构并不是一种先验的知识，应该由神经网络本身来捕获。多亏了

　　　　$\begin{aligned}\mathbf{H}_{G}^{(K)}=& \mathrm{SMG}_{k_{L}}\left(\mathbf{H}_{G}^{\left(K-k_{L}\right)}, \mathbf{A}_{G}, \mathbf{M}_{G_{S_{L}}}\right) \\=& \mathrm{SMG}_{k_{L}}(\mathrm { SMG } _ { k _ { L - 1 } } (\ldots \mathrm{SMG}_{k_{1}}(\mathbf{X}_{G}, \mathbf{A}_{G}, \mathbf{M}_{G_{S_{1}}}),&\left.\left.\mathbf{A}_{G}, \mathbf{M}_{G_{S_{L-1}}}\right), \mathbf{A}_{G}, \mathbf{M}_{G_{S_{L}}}\right) \\=& \mathrm{SMG}_{K}\left(\mathbf{X}_{G}, \mathbf{A}_{G}, \prod\limits _{i=1}^{L} \mathbf{M}_{G_{S_{i}}}\right) \\=& \mathrm{SMG}_{K}\left(\mathbf{X}_{G}, \mathbf{A}_{G}, \mathbf{M}_{G}\right)\end{aligned}$

　　这意味着任何需要的堆叠 L 层的 SMGs 都等同于相同数量的 SMG 层，具有掩码分配 $ \mathbf{M}_{G}=\|_{i=1}^{L} \mathbf{M}_{G_{S_{i}}}$。我们可以通过适当的 $\mathbf{M}_{G}$ 分配获得所需的堆叠L SMGs。然后，将捕获层次结构的问题转换为寻找 $\mathbf{M}_{G}$ 的分配。

　　$\mathbf{M}_{G}$ 的灵活性使 SMG 能够提取更丰富的结构信息，而不仅仅是一般的基于密集聚合的 GNNs。我们已经证明了单层 SMG 只能捕获子图，而多层 SMG 可以捕获图的层次结构。当 $L>1$ 和 $G_{S_{i}}$ 被限制为 $G_{S_{i-1}}$ 的一个子图时，所有 $i \in[L-1]$，SMG的工作方式类似于基于 top-k 的图池[3,7,14,15]，它迭代地一层一层地删除一些节点和相关的边。但是，图1中所示的不同部分的交互不能被这种方案捕获，因为以前跳过的下层节点不会涉及到更高的层中。

3.3 Mask Assignments Computations

　　下述讲述使用 $\mathrm{GNN}-w$ 学习 $\mathbf{M}_{G}$ 的分配，第 $k$ 层中节点 $v$ 的值为：

　　　　$\begin{aligned}\mathbf{M}_{\mathbf{G} k, v}=& m_{v}^{(k)} \\=& \operatorname{MLP}^{(k)}(\operatorname { R e L U } ([\mathbf{L}_{1}^{(k)}(m_{v}^{(k-1)} \mathbf{h}_{v}^{(k-1)}) \|\sum_{u \in \mathcal{N}(v)} \mathbf{L}_{2}^{(k)}(m_{u}^{(k-1)} \mathbf{h}_{u}^{(k-1)})]))\end{aligned}\quad\quad\quad\quad(4)$

　　其中，$\mathbf{L}_{1}^{(k)}$ 和 $\mathbf{L}_{2}^{(k)}$ 为仿射映射【实际上代码并没有体现】；$\sum\limits _{u \in \mathcal{N}(v)} \mathbf{L}_{2}^{(k)}\left(m_{u}^{(k-1)} \mathbf{h}_{u}^{(k-1)}\right)$ 其实就是一个消息传递（采用 ''add'' 作为 aggragation），且第一次输入的特征矩阵并不是原始特征，而是经线性映射的特征，注意此处消息聚合并没有加上自环。

　　具体看代码：

class WeightConv1(MessagePassing):
    def __init__(self, in_channels, hid_channels, out_channels=1, aggr='add', bias=True,
                 **kwargs):
        super(WeightConv1, self).__init__(aggr=aggr, **kwargs)
        self.lin1 = torch.nn.Linear(in_channels, hid_channels, bias=bias)     #[128,128]
        self.lin2 = torch.nn.Linear(in_channels, hid_channels, bias=bias)       #[128,128]
        self.lin3 = torch.nn.Linear(hid_channels * 2, hid_channels, bias=bias)     #[256,128]
        self.lin4 = torch.nn.Linear(hid_channels, out_channels, bias=bias)         # [128,128]

    def forward(self, x, edge_index, mask=None, edge_weight=None, size=None):
        edge_index, _ = remove_self_loops(edge_index)
        if mask is not None:
            x = x * mask
        h = self.lin1(x)
        return self.propagate(edge_index, size=size, x=x, h=h,edge_weight=edge_weight)
                              
    def message(self, h_j, edge_weight):    #edge_weight  = None
        print("in message")
        return h_j if edge_weight is None else edge_weight.view(-1, 1) * h_j

    def update(self, aggr_out, x):
        print("in update")
        weight = torch.cat([aggr_out, self.lin2(x)], dim=-1)
        weight = F.relu(weight)
        weight = self.lin3(weight)
        weight = F.relu(weight)
        weight = self.lin4(weight)
        weight = torch.sigmoid(weight)    #mask.shape = [Batch_N, 128])
        return weight

　　Note：上述 $\mathbf{L}_{1}^{(k)}$ 和 $\mathbf{L}_{2}^{(k)}$ 以及 MLP 中的常量部分（即 bias ）是被需要的，否则 $m_{v}^{(k-1)} \mathbf{h}_{v}^{(k-1)}=\mathbf{0}$ 和 $m_{u}^{(k-1)} \mathbf{h}_{u}^{(k-1)}=\mathbf{0}$，并且 $m_{v}^{(k)}$ 将长期固定为 $0.5$ 。

　　每个节点上的 $m_{v}^{(k)}$ 值 是从 $0$ 到 $1$ ，并不是像预期的离散值   $0$ 或 $1$ 。在 SMG 图层中，对于 $i \in \hat{\mathcal{N}}(v)$ 的 $m_{i}^{(k)} \in[0,1]$ 有 $\mathbf{h}_{v}^{(k)}=f\left(\left\{m_{i}^{(k)} \mid i \in \hat{\mathcal{N}}(v)\right\}\right)=\operatorname{ReLU}\left(\mathbf{W}_{1}^{(k)} m_{v}^{(k)}\left[\mathbf{h}_{v}^{(k-1)} \|\right.\right. \left.\left.\sum_{u \in \mathcal{N}(v)} m_{u}^{(k)} \mathbf{h}_{u}^{(k-1)}\right]\right)$ 。因此对于 $i \in \hat{\mathcal{N}}(v)$，我们有 $\lim _{m_{i}^{(k)} \rightarrow 0^{+}} f\left(m_{i}^{(k)}, \ldots\right)=f(0, \ldots) $ 和 $\lim _{m_{i}^{(k)} \rightarrow 1^{-}} f\left(m_{i}^{(k)}, \ldots\right)=f(1, \ldots)$，使它有可能被使用 $m_{v}^{(k)}$ 去近似于掩码值 $0$ 或 $1$。

　　soft-mask 的好处是考虑到了权重。由于 $\mathbf{h}_{v}^{(k)}$ 表示一个基于 $v$ 的 k-hop子树，该子树捕获了基于 $v$ 的局部 k-hop 子结构的结构信息，$m_{v}^{(k)}$ 与 $\mathbf{h}_{v}^{(k)}$ 相乘给出了以下聚合操作的子结构的权重。对于权值为 $0$ 的节点，相当于删除边。为了保持  zero invariant，使用 SUM 作为 Readout 函数。并在最后一层使用跳跃连接：

　　　　$\mathbf{h}_{G}=\|_{k=1}^{K}\left(\sum\limits _{i=1}^{N} \mathbf{h}_{i}^{(k)}\right) \quad\quad\quad(5)$

　　Equation 5 利用来自不同层的节点表示来计算整个图表示 $\mathbf{h}_{G}$。由于第 $k$ 层 $\mathbf{h}_{v}^{(k)}$ 中的节点表示用权重 $m_{v}^{(k)}$ 编码 k-hop子结构，当实现读出函数作为 Equation 5 时，$\mathbf{h}_{v}^{(k)}$ 的所有子结构都考虑了不同跳跃的权重。

3.4 Multi-channel Soft-mask GNN Model

　　将 soft-mask 改成多通道使得 $m_{v}^{(k)} \in(0,1)^{d}$ 【特征级】，SMG层（Equation 3）被改写为：

　　　　$\begin{aligned}\mathbf{h}_{v}^{(k)}=& \operatorname{ReLU}(m _ { v } ^ { ( k ) } \odot \mathbf { W } _ { 2 } ^ { ( k ) } [\mathbf{h}_{v}^{(k-1)} \|\sum\limits _{u \in \mathcal{N}(v)} m_{u}^{(k)} \odot \mathbf{h}_{u}^{(k-1)}])\end{aligned} \quad\quad\quad(6)$

4 Experiments

Graph Classification Task

　　

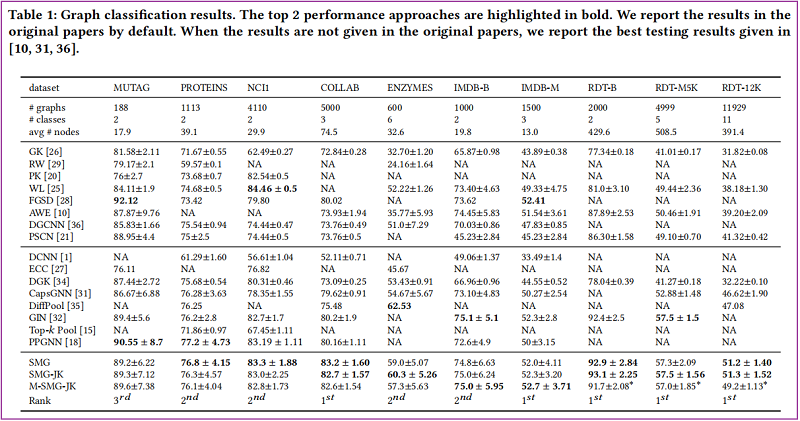
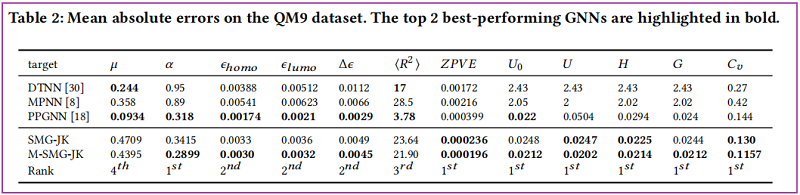
Graph Regression Task

　　

5 Conclusion

　　通过有效地跳过图的不相关部分，我们提出了软掩模GNN(SMG)层，它从一系列子图序列中学习图的表示。我们展示了它显式地提取所需的子结构或层次结构的能力。在基准图分类和图回归数据集上的实验结果表明，SMG获得了显著的改进，掩模的可视化提供了模型学习到的结构的可解释性。

 

 

==========