论文解读（PNA）《Principal Neighbourhood Aggregation for Graph Nets》

论文信息

论文标题：Principal Neighbourhood Aggregation for Graph Nets
论文作者：Gabriele Corso, Luca Cavalleri, Dominique Beaini, Pietro Liò, Petar Veličković
论文来源：2020,NeurIPS
论文地址：download 
论文代码：download 

1 Introduction

 　　越搞越复杂........................................................

2 Principal Neighbourhood Aggregation

　　在本节中，我们首先解释并发使用多个聚合器背后的动机。然后，我们提出了基于度的尺度器的想法，链接到之前关于GNN表达性的相关工作。最后，我们详细介绍了利用所提出的主邻域聚合的图卷积层的设计

2.1 Proposed aggregators

　　在 Figure 1 中，我们观察到当使用单个 GNN 层时，不同的聚合器如何无法区分不同的消息。

　　

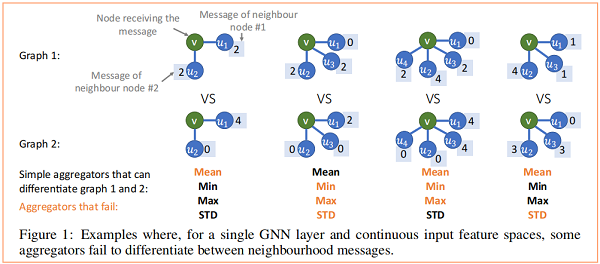
　　Theorem 1 (Number of aggregators needed). In order to discriminate between multisets of size n whose underlying set is $\mathbb{R}$ , at least $n$ aggregators are needed.

　　Proposition 1 (Moments of the multiset). The moments of a multiset (as defined in Equation 4) exhibit a valid example using $n$ aggregators.

　　Theorem 1 证明了所使用的独立聚合器的数量是 GNNs 表达性的一个限制因素。为了通过经验证明这一点，我们利用了四种聚合器，即 mean、maximum、minimum, standard deviation 。此外，我们注意到这可以扩展到 normalized moment aggregators ，它允许在节点的度较高时提取高级分布信息。

Mean aggregation $\mu\left(X^{l}\right)$

　　　　$\mu(X)=\mathbb{E}[X] \quad, \quad \mu_{i}\left(X^{l}\right)=\frac{1}{d_{i}} \sum\limits _{j \in N(i)} X_{j}^{l}\quad\quad\quad(1)$

Maximum and minimum aggregations $\max \left(X^{l}\right)$ ，$\min \left(X^{l}\right)$

 　　　　$\max _{i}\left(X^{l}\right)=\max _{j \in N(i)} X_{j}^{l}     \quad, \quad \min _{i}\left(X^{l}\right)=\min _{j \in N(i)} X_{j}^{l} \quad\quad\quad(3)$

Standard deviation aggregation  $\sigma\left(X^{l}\right)$

　　　　$\sigma(X)=\sqrt{\mathbb{E}\left[X^{2}\right]-\mathbb{E}[X]^{2}} \quad, \quad \sigma_{i}\left(X^{l}\right)=\sqrt{\operatorname{ReLU}\left(\mu _ { i } \left(X^{\left.\left.l^{2}\right)-\mu_{i}\left(X^{l}\right)^{2}\right)+\epsilon}\right.\right.}\quad\quad\quad(3)$

Normalized moments aggregation $M_{n}\left(X^{l}\right)$

　　　　$M_{n}(X)=\sqrt[n]{\mathbb{E}\left[(X-\mu)^{n}\right]}, \quad n>1\quad\quad\quad(4)$

2.2 Degree-based scalers

　　先前工作建议使用 sum aggregation，本文通过将和聚合器表示为一个平均聚合器和一个线性度放大标量器的组成来推广他们的方法 $S_{\mathrm{amp}}(d)=d$。

　　Theorem 2 (Injective functions on countable multisets). The mean aggregation composed with any scaling linear to an injective function on the neighbourhood size can generate injective functions on bounded multisets of countable elements.

　　最近的工作表明，summation 聚合并不能很好地推广到看不见的图中。一个原因是，度的微小变化将会导致信息和梯度被指数放大/衰减（每一层的线性放大将会导致多层后的指数放大）。本文建议使用对数放大的 $S \propto \log (d+1)$ 来减少这种影响。这个场景展示了对数尺度如何更好地区分影响者和追随者节点接收到的消息。

　　使用对数标量器的进一步动机是为了更好地描述给定节点的邻域影响。假设我们有一个社交网络，其中节点 A、B和C分别有500万、100万和100名追随者：在线性尺度上，节点 B 和  C 比 A 和 B 更接近；然而，这并不能准确地模拟它们的相对影响。这个场景展示了对数尺度如何更好地区分影响者和关注者节点接收到的消息。

　　我们提出了公式 5 中提出的 logarithmic scaler $S_{\text {amp }}$，其中 $\delta$ 是在训练集上计算的一个归一化参数，$d$ 是节点接收消息的度。

 　　　　$S_{\text {amp }}(d)=\frac{\log (d+1)}{\delta} \quad, \quad \delta=\frac{1}{|\operatorname{train}|} \sum_{i \in \text { train }} \log \left(d_{i}+1\right)\quad\quad\quad(5)$

　　我们在方程 $6$ 中进一步推广了这个标度，其中 $\alpha$ 是一个变量参数，衰减为负，放大为正，无标度为零。$S(d)$ 的其他定义也可以使用，如线性缩放，只要该函数对 $d>0$ 是单射的。

　　　　$S(d, \alpha)=\left(\frac{\log (d+1)}{\delta}\right)^{\alpha}, \quad d>0, \quad-1 \leq \alpha \leq 1\quad\quad\quad(6)$

2.3 Combined aggregation

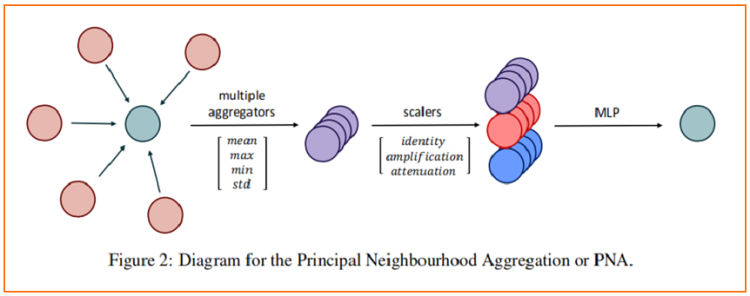
　　我们结合了前几节中介绍的 aggregator 和 scaler，获得了主邻域聚合 ( PNA )。

　　　　$\bigoplus=\underbrace{\left[\begin{array}{c}I \\S(D, \alpha=1) \\S(D, \alpha=-1)\end{array}\right]}_{\text {scalers }} \otimes \underbrace{\left[\begin{array}{c}\mu \\\sigma \\\max \\\min\end{array}\right]}_{\text {aggregators }}\quad\quad\quad(7)$

　　如前所述，像社交网络这样的高阶图可以从进一步的聚合器中获益（例如，使用 $Eq.4$ 中提出的矩）。我们将 PNA 算子插入到消息传递神经网络[17]的框架中，得到以下GNN层：

　　　　$X_{i}^{(t+1)}=U\left(X_{i}^{(t)}, \bigoplus_{(j, i) \in E} M\left(X_{i}^{(t)}, E_{j \rightarrow i}, X_{j}^{(t)}\right)\right)\quad\quad\quad(8)$

　　其中，$E_{j \rightarrow i}$ 是 edge $(j, i)$ 的特征，$M$ 和 $U$ 是神经网络，$U$ 减少了所连接的消息 [ $\mathbb{R}^{13F}$ 到 $\mathbb{R}^{F}$ ]。我们采用多座塔来提高计算复杂度和泛化性能。

　　

3 Conclusion

　　看看就行......................