论文解读（MaskGAE）《MaskGAE: Masked Graph Modeling Meets Graph Autoencoders》

论文信息

论文标题：MaskGAE: Masked Graph Modeling Meets Graph Autoencoders
论文作者：Jintang Li, Ruofan Wu, Wangbin Sun, Liang Chen, Sheng Tian......
论文来源：2022,arXiv
论文地址：download 
论文代码：download

1 Introduction

 　　MAE 在图上的应用。

2 Related work and Motivation

2.1 GAE 

　　GAEs采用了经典的编码器-解码器框架，旨在通过优化以下二进制交叉熵损失，从编码图的低维表示中进行解码：

　　　　$\mathcal{L}_{\mathrm{GAEs}}=-\left(\frac{1}{\left|\mathcal{E}^{+}\right|} \sum\limits _{(u, v) \in \mathcal{E}^{+}} \log h_{\omega}\left(z_{u}, z_{v}\right)+\frac{1}{\left|\mathcal{E}^{-}\right|} \sum\limits _{\left(u^{\prime}, v^{\prime}\right) \in \mathcal{E}^{-}} \log \left(1-h_{\omega}\left(z_{u^{\prime}}, z_{v^{\prime}}\right)\right)\right)$

　　其中，$\mathcal{z}$ 代表低维隐表示，$f_{\theta}$ 代表参数为  $\theta$ 的 GNN encoder，$h_{\omega}$ 代表参数为  $\omega$ 的 GNN decoder，$\mathcal{E}^{+}$ 代表  positive edges ，$\mathcal{E}^{-}$ 代表 negative edges 。

2.2 Motivation

　　按照互信息的思想：希望最大化 k-hop 节点对子图之间的一致性，但是伴随着 $K$ 值变大，过平滑的问题越发明显，此时子图大小对节点表示的学习不利。因此有：

　　Proposition 1：

　　

 　　分析了一堆废话................

　　后面呢，必然出现解决过平滑的策略。

　　Recall：解决过平湖的策略

• • 残差；
  • 谱图理论；
  • 多尺度信息；
  • 边删除；

3 Method：MaskGAE 

　　我们提出了 MGM 代理任务的 MaskGAE 框架：

　　

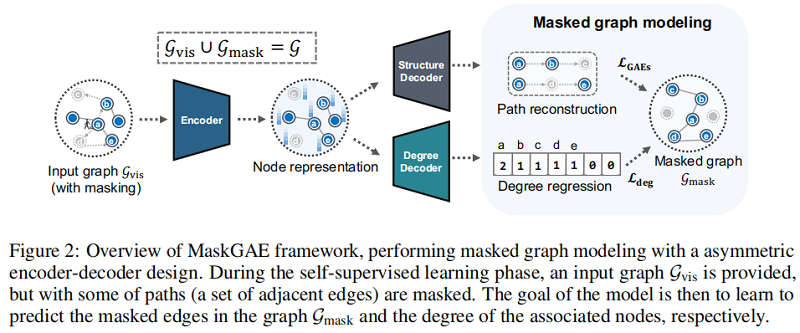
　　出发点：MGM

　　　　$\mathcal{G}_{\text {mask }} \cup   \mathcal{G}_{\text {vis }}=\mathcal{G}$

　　　　$\mathcal{G}_{\text {mask }}=   \left(\mathcal{E}_{\text {mask }}, \mathcal{V}\right)$

3.1 Masking strategy

Edge-wise random masking $(\mathcal{T}_{\text {edge }}$

　　　　$\mathcal{E}_{\text {mask }} \sim \operatorname{Bernoulli}(p)$

Path-wise random masking $(\mathcal{T}_{\text {path}}$

　　　　$\mathcal{E}_{\text {mask }} \sim \operatorname{Random} \operatorname{Walk}\left(\mathcal{R}, n_{\text {walk }}, l_{\text {walk }}\right)$

　　其中，$\mathcal{R} \subseteq \mathcal{V}$ 是从图中采样的一组根节点，$n_{\text {walk }}$ 为每个节点的行走次数，$l_{\text {walk }}$ 为行走长度。

　　在这里，我们遵循度分布，抽样了一个节点的子集（例如，50%），没有替换作为根节点 $\mathcal{R}$。这样的采样也可以防止图中存在的潜在的长尾偏差（即，更多的屏蔽边是那些属于高度节点的边）。

3.2 Encoder

• GCN Encoder    
• SAGE Encoder
• GAT Encoder

3.2 Decoder

Structure decoder

　　　　$​h_{\omega}\left(z_{i}, z_{j}\right)=\operatorname{Sigmoid}\left(z_{i}^{\mathrm{T}} z_{j}\right)$

　　　　$​h_{\omega}\left(z_{i}, z_{j}\right)=\operatorname{Sigmoid}\left(\operatorname{MLP}\left(z_{i} \circ z_{j}\right)\right)$

Degree decoder

　　　　$g_{\phi}\left(z_{v}\right)=\operatorname{MLP}\left(z_{v}\right)$

3.3 Learning objective

　　损失函数包括：

• • Reconstruction loss：计算的是掩码边 $\mathcal{E}^{+}=\mathcal{E}_{\text {mask }}$   的重构损失；
  • Regression loss：衡量的是节点度的预测与掩蔽图中原始节点度的匹配程度：

 　　　　　　$\mathcal{L}_{\mathrm{deg}}=\frac{1}{|\mathcal{V}|} \sum\limits _{v \in \mathcal{V}}\left\|g_{\phi}\left(z_{v}\right)-\operatorname{deg}_{\text {mask }}(v)\right\|_{F}^{2}$

　　其中，$\operatorname{deg}_{\text {mask }}$ 代表的是掩码图 $\mathcal{G}_{\text {mask }}$ 的节点度。

　　因此，总体损失为：

　　　　$\mathcal{L}=\mathcal{L}_{\mathrm{GAEs}}+\alpha \mathcal{L}_{\mathrm{deg}}$

4 Experiments

Link prediction

　　

node classifification 

　　

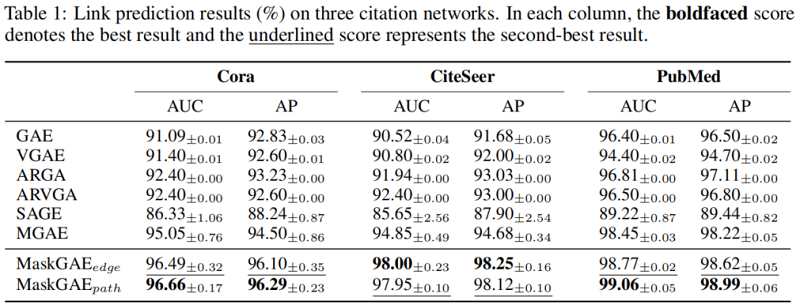
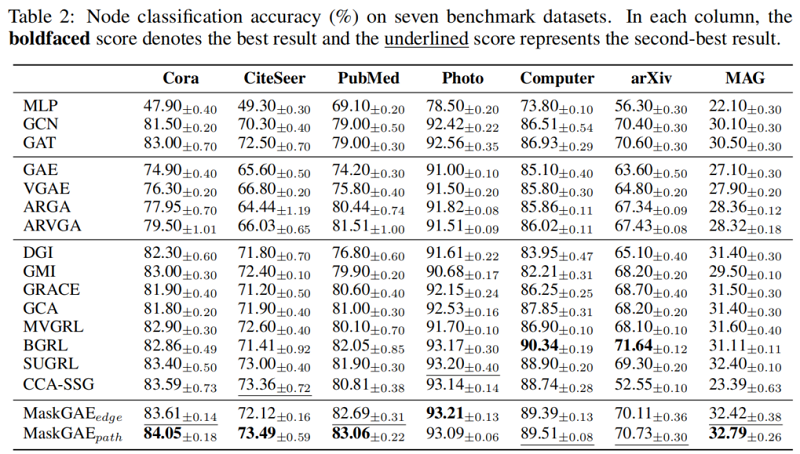
5 Conclusion

　　在这项工作中，我们首次研究了掩蔽图建模(MGM)，并提出了MaskGAE，一个基于理论基础的自我监督学习框架，以 MGM 作为一个有原则的借口任务。我们的工作在理论上是基于以下理由：(i)气体本质上是对比学习，使与链接边相关的配对子图视图之间的互信息最大化；(ii)MGM可以有利于互信息最大化，因为掩蔽显著减少了两个子图视图之间的冗余。特别是，我们还提出了一种路径掩蔽策略，以促进米高梅的任务。在我们的实验中，MaskGAE 比 GAE 表现出显著改善的性能，并且在链路预测和节点分类基准上与强基线相当或更好。