论文信息
论文标题:Simple and Deep Graph Convolutional Networks
论文作者:Ming Chen, Zhewei Wei, Zengfeng Huang, Bolin Ding, Yaliang Li
论文来源:2020,PMLR
论文地址:download
论文代码:download
1 Introduction
目前的 GNNs 是浅层的神经网络,且存在过平滑(over-smoothing)的问题。本文对 朴素版本的 GCN 加上两种有效的技巧: Initial residual 和 Identity mapping 。
出发点:
2 Relatework
2.1 Vanilla GCN
Vanilla GCN 建议可以进一步用拉普拉斯的 K 次多项式来逼近图的卷积运算:
Ugθ(Λ)UTx≈U(∑Kℓ=0θℓΛℓ)U⊤x=(∑Kℓ=0θℓLℓ)x
回顾:
二代GCN中:
gθ(Λ)=K∑l=0θlΛl
Ugθ(Λ)UTx=UK∑l=0θlΛlUTx=K∑l=0θlUΛlUTx=K∑l=0θlLlx
其中:
L=In−D−1/2AD−1/2 是一个 对称正半定矩阵 ,可以进行特征分解 L=UΛUT 。
vanilla GCN (Kipf & Welling, 2017) 设置 K=1,θ0=2θ,θ1=−θ,然后使用 renormalization trick 将矩阵 I+D−1/2AD−1/2 替换为 ~P=~D−1/2~A~D−1/2=(D+In)−1/2(A+In)(D+In)−1/2,得到图卷积层为:
H(ℓ+1)=σ(~PH(ℓ)W(ℓ))(1)
2.2 SGC
SGC 结果表明,通过叠加 K 层,GCN对应于 ~G 的图谱域上的一个固定的 K 阶多项式滤波器。
特别地,让 ~L=In−~D−1/2~A~D−1/2 表示自环图 ~G 的归一化图拉普拉斯矩阵。因此,对信号 x 应用 k 层GCN对应于 (~D−1/2~A~D−1/2)Kx=(In−~L)Kx。还表明,通过向每个节点添加一个自循环,~L 有效地缩小了底层的图谱。
2.3 APPNP
采用 k 阶固定滤波器。设 fθ(X) 表示特征矩阵 X 上的两层全连通神经网络的输出,PPNP 的模型定义为
H=α(In−(1−α)~A)−1fθ(X)(2)
由于 Personalized PageRank 的特性,这种滤波器保持了局部性,因此适用于分类任务。 (Klicpera et al., 2019a) 还相应提出了 APPNP ,一种替换 α(In−(1−α)~A)−1 为截断幂迭代(truncated power iteration)。在形式上,具有 k 跳聚合的 APPNP 被定义为:
H(ℓ+1)=(1−α)~PH(ℓ)+αH(0)(3)
其中,H(0)=fθ(X)。通过解耦特征转换和传播,PPNP和APPNP可以在不增加神经网络层数的情况下聚合来自多跳邻居的信息。
2.4 JKNet
在最后一层,JKNet 将所有层的表示 [H(1),…,H(K)] 拼接起来 ,来学习对不同的图子结构的不同阶数的表示。
JKNet 说明了:
-
- 一个 K 层 vanilla GCN 模型模拟了自环图 ~G 中 K 步的随机游走;
- 通过结合前一层的所有表示,JKNet 缓解了过平滑的问题;
2.5 DropEdge
将自环图 ~G 中的部分边删除延缓了过平湖的问题,令 ~Pdrop 表示 随机去除一些边的重整化图卷积矩阵,将具有 DropEdge 的普通GCN定义为:
H(ℓ+1)=σ(~PdropH(ℓ)W(ℓ))(4)
3 GCNII Model
众所周知(Wuetal.,2019),通过叠加 K 层,vanilla GCN 在 ~G 的图谱域上模拟了一个固定系数 θ 的多项式滤波器 (∑Kℓ=0θℓ~Lℓ)X。固定的系数限制了多层GCN模型的表达能力,从而导致了过度平滑。为了将GCN扩展到一个真正的深度模型,我们需要使GCN能够表达一个具有任意系数的 K 阶多项式滤波器。我们证明了这可以通过两种简单的技术来实现:Initial residual connection 和 Identity mapping。
在形式上,我们将GCNII 的第 ℓ 层定义为:
H(ℓ+1)=σ(((1−αℓ)~PH(ℓ)+αℓH(0))((1−βℓ)In+βℓW(ℓ)))(5)
其中,αℓ 和 βℓ 代表着超参数,~P=~D−1/2~A~D−1/2 是经 renormalization trick 的图卷积矩阵。
对比 vanilla GCN ,
-
- 1) 我们将平滑的表示 ~PH(ℓ) 与第一层 H(0) 的初始残差连接相结合;
- 2) 我们在第 ℓ 个权重矩阵 W(ℓ) 中添加一个恒等矩阵映射;
Initial residual connection
(Kipf & Welling, 2017) 提出了结合平滑表示法 ~PH(ℓ) 和 H(ℓ) 的残差连接,这被证明了只是部分缓解过平滑问题,且当层数堆叠多层后依旧存在着性能骤降的问题。
受 (Hardt & Ma, 2017) 提出的 linear ResNet :H(ℓ+1)=H(ℓ)(W(ℓ)+In) 启发,它满足 1) 最优的权重矩阵 W(l) 具有较小的范数;2) 唯一的临界点是全局最小值。第一个性质允许我们进行在 Wℓ 上很强的正则化处理,避免过拟合,而后者在训练数据有限的半监督任务中是可取的。
(Oono & Suzuki, 2020) 从理论上证明了 k 层GCNs的节点特征会收敛到子空间并导致信息损失。特别地,收敛速度取决于sK,其中 s 是权值矩阵 W(ℓ),ℓ=0,…,K−1 的最大奇异值。通过替换 W(ℓ) 替换为 (1−βℓ)In+βℓW(ℓ),并对 W(ℓ) 进行正则化,我们强制 W(ℓ) 的范数很小。因此,在 W(ℓ) 的奇异值将接近于1。因此,最大奇异值 s 也将接近于 1,这意味着 sK 较大,信息损失被减轻。
设置 βℓ 的原则是确保权重矩阵的衰减随着我们堆叠更多的层而自适应地增加。在实践中,我们设置了 βℓ=log(λℓ+1)≈λℓ,其中 λ 是一个超参数。
Connection to iterative shrinkage-thresholding
考虑了 LASSO 的目标函数:
minx∈Rn12∥Bx−y∥22+λ∥x∥1
其中,x 是我们需要恢复的信号,B 作为测量矩阵,y 是观测变量。本文中 y 是节点原始特征,x 是网络学习到的表示。
上述问题是稀疏编码问题,迭代收缩阈值算法是解决上述优化问题的有效方法。第 t+1 次迭代更新为:
xt+1=Pμtλ(xt−μtBTBxt+μtBTy)
其中,μt 是步长,Pβ(⋅) 是软阈值化函数(β>0):
Pθ(z)=⎧⎪⎨⎪⎩z−θ, if z≥θ0, if |z|<θz+θ, if z≤−θ
接着,重参数化 −BTB 为 W,上面的更新公式与我们的方法中使用的更新公式非常相似。具体的,我们有 xt+1=Pμtλ((I+μtW)xt+μtBTy),其中 μtBTy 代表着 初始残差连接,I+μtW 代表着 恒等映射。
4 Spectral Analysis
4.1 Spectral analysis of multi-layer GCN
我们考虑以下具有残差连接的GCN模型:
H(ℓ+1)=σ((~PH(ℓ)+H(ℓ))W(ℓ)).(6)
其中,~P=~D−1/2~A~D−1/2 是经过 renormalization trick 的图卷积矩阵。(Wang et al., 2019) 指出 Eq.6 是概率转移矩阵为 In+~D−1/2~A~D−1/22 的懒惰随机游走。这种懒惰随机游走最终收敛到平稳状态,从而导致过度平滑。
现在我们推导了平稳向量的封闭形式,并分析了这种收敛速度。我们的分析表明,单个节点的收敛率取决于它的度,我们进行了实验来支持这一理论发现。特别地,我们有以下定理。


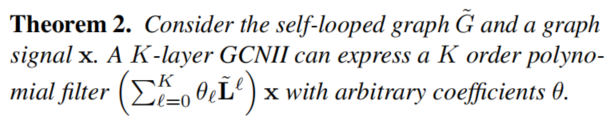
5 GCNII*
H(ℓ+1)=σ((1−αℓ)~PH(ℓ)((1−βℓ)In+βℓW(ℓ)1)++αℓH(0)((1−βℓ)In+βℓW(ℓ)2))
6 Experiments
Semi-supervised Node Classifification
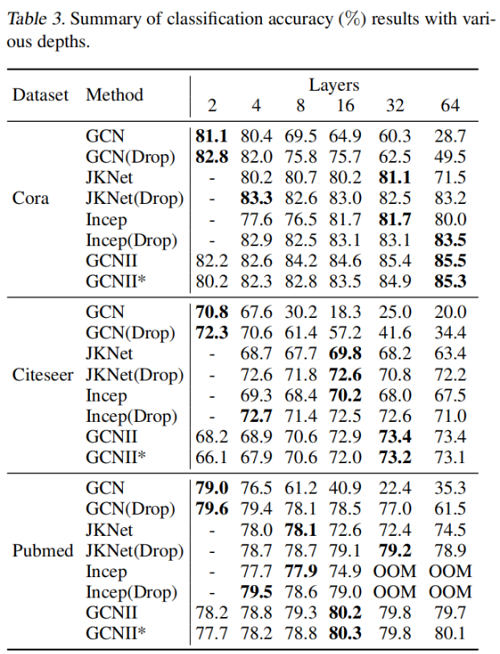
Full-Supervised Node Classifification

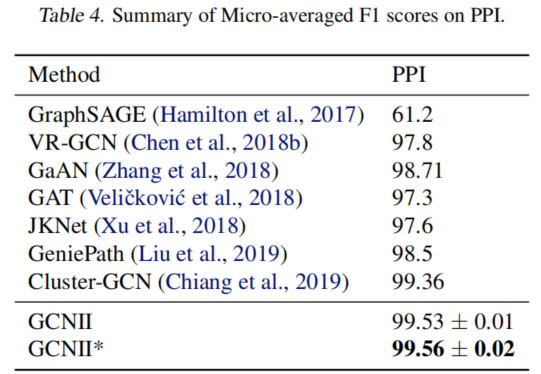
Inductive Learning


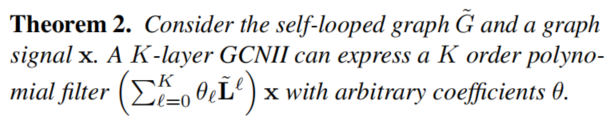






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识?