论文解读（LGAE）《Simple and Effective Graph Autoencoders with One-Hop Linear Models》

论文信息

论文标题：Simple and Effective Graph Autoencoders with One-Hop Linear Models
论文作者：Guillaume Salha, Romain Hennequin, Michalis Vazirgiannis
论文来源：2020, ECML/PKDD
论文地址：download 
论文代码：download

1 Introduction

 　　线性图自编码器。

　　感觉这篇论文就是做着玩玩的~~~~~

2 Preliminaries

2.1 Graph Autoencoders

　　框架：

　　　　$\hat{A}=\sigma\left(Z Z^{T}\right) \text { with } Z=\operatorname{GNN}(\mathrm{A})\quad\quad\quad(1)$

　　损失函数：

　　　　$\mathcal{L}^{\mathrm{AE}}=-\frac{1}{n^{2}} \sum\limits _{(i, j) \in \mathcal{V} \times \mathcal{V}}\left[A_{i j} \log \hat{A}_{i j}+\left(1-A_{i j}\right) \log \left(1-\hat{A}_{i j}\right)\right]\quad\quad\quad(2)$

2.2 Graph Variational Autoencoders

　　框架：

　　　　$q(Z \mid A)=\prod\limits _{i=1}^{n} q\left(z_{i} \mid A\right) \text { with } q\left(z_{i} \mid A\right)=\mathcal{N}\left(z_{i} \mid \mu_{i}, \operatorname{diag}\left(\sigma_{i}^{2}\right)\right)\quad\quad\quad(3)$

　　　　$p(A \mid Z)=\prod\limits _{i=1}^{n} \prod\limits _{j=1}^{n} p\left(A_{i j} \mid z_{i}, z_{j}\right) \text { with } p\left(A_{i j}=1 \mid z_{i}, z_{j}\right)=\hat{A}_{i j}=\sigma\left(z_{i}^{T} z_{j}\right)\quad\quad\quad(4)$

　　损失函数：

　　　　$\mathcal{L}^{\mathrm{VAE}}=\mathbb{E}_{q(Z \mid A)}[\log p(A \mid Z)]-\mathcal{D}_{K L}(q(Z \mid A) \| p(Z))\quad\quad\quad(5)$

3 Method

　　框架图：

　　

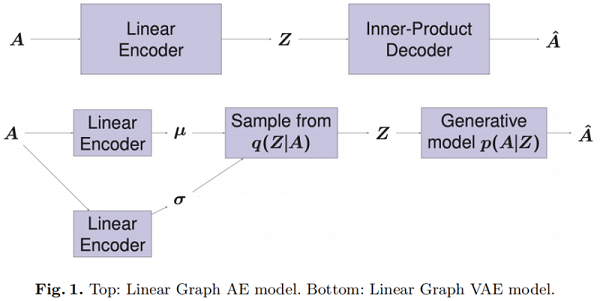
3.1 Linear Graph AE

　　本文的线性图自编码器为：

　　　　$Z=\tilde{A} W, \text { then } \hat{A}=\sigma\left(Z Z^{T}\right)\quad\quad\quad(7)$

　　其中，$\tilde{A}=D^{-1 / 2}\left(A+I_{n}\right) D^{-1 / 2}$。

　　不同之处：

• • 忽略了高阶信息；
  • 不需要激活函数；

　　不使用高阶信息和激活函数对性能影响小。

　　当然也可以考虑使用图特征信息：

　　　　$Z=\tilde{A} X W  \quad\quad\quad(8)$

3.2 Linear Graph VAE

　　线性图变分自编码器：

　　　　$\begin{array}{l}\mu=\tilde{A} W_{\mu} \\\log \sigma=\tilde{A} W_{\sigma}\end{array}\quad\quad\quad(9)$

　　其中，$W_{\mu}\in \mathbb{R} ^{n\times d}$、$W_{\sigma}\in \mathbb{R} ^{n\times d}$

　　获得均值和方差后，可计算隐表示 $z_i$：

　　　　$\forall i \in \mathcal{V}, z_{i} \sim \mathcal{N}\left(\mu_{i}, \operatorname{diag}\left(\sigma_{i}^{2}\right)\right) \quad\quad\quad(10)$

　　对于包含特征矩阵 $X$ 的图时，可以计算：

　　　　$\begin{array}{l}\mu=\tilde{A} X W_{\mu} \\ \log \sigma=\tilde{A} X W_{\sigma}\end{array}\quad\quad\quad(11)$

4 Experiments

链接预测

　　

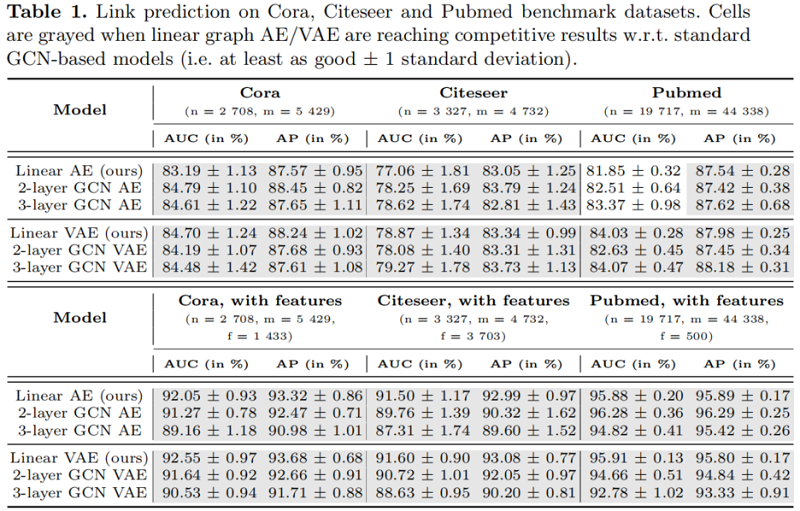
节点聚类

　　

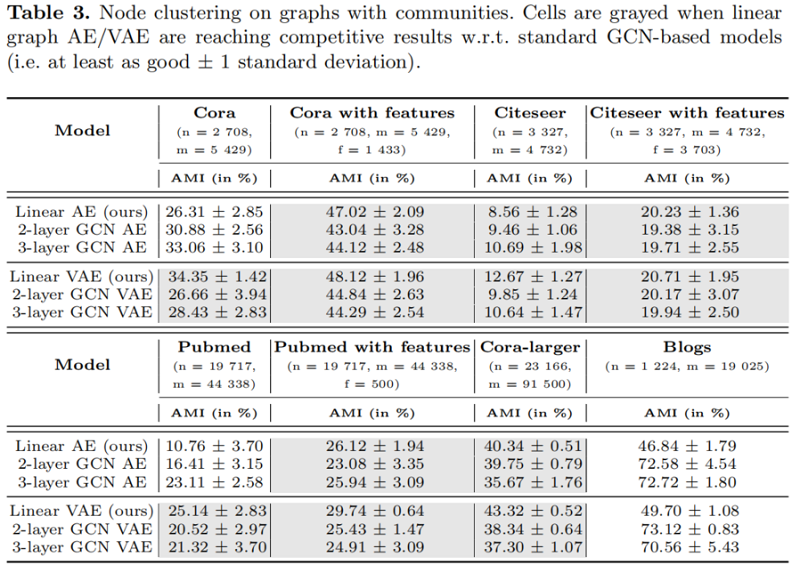
5 Conclusion

　　图自编码器(AE)、图变分自编码器(VAE)及其大部分扩展都依赖于多层图卷积网络(GCN)编码器来学习节点嵌入表示。在本文中，我们强调，尽管它们普遍使用，这些编码器往往是不必要的复杂。在这个方向上，我们引入并研究了这些模型的明显更简单的版本，利用了一跳线性编码策略。使用这些替代模型，我们达到了竞争性的经验性能w.r.t.基于GCN的图AE和VAE在许多真实世界的图上。我们确定了简单的一跳线性编码器作为多层gcn的有效替代方案的设置，并作为在进入更复杂的模型之前实现的第一个相关基线。我们还质疑了重复使用相同的稀疏中等大小的数据集(Cora，Citeseer，Pubmed)来评估和比较复杂的图AE和VAE模型的相关性。

 

修改历史

2022-06-28 创建文章

 

论文解读目录