论文解读（SAIL）《SAIL: Self-Augmented Graph Contrastive Learning》

论文信息

论文标题：SAIL: Self-Augmented Graph Contrastive Learning
论文作者：Lu Yu, Shichao Pei, Lizhong Ding, Jun Zhou, Longfei Li, Chuxu Zhang, Xiangliang Zhang
论文来源：2022,AAAI
论文地址：download
论文代码：download

1 Introduction

　　GNNs 的性能取决于节点特征的平滑性和图结构的局部性。

　　为了平滑通过图拓扑和节点特征测量的节点接近度差异，我们提出了一种新的自增强图对比学习框架，具有两个互补的自提取正则化模块，即图内和图间知识蒸馏。

2 Methodology

　　深度图编码器 $\Phi$ 通常存在过平滑问题。在这项工作中，我们实例化了一个具有单层的 GNN，以验证所提出的方法在学习具有浅层邻居的合格节点表示方面的有效性。但是下一节中的分析结果可以很容易地扩展到更深层次的GNN。本文中使用的图神经编码器的定义为：

　　　　$\begin{array}{l}\tilde{\mathbf{A}}=D^{-\frac{1}{2}}(A+I) D^{-\frac{1}{2}} \\\Phi(\mathbf{X}, \tilde{\mathbf{A}})=\sigma\left(\tilde{\mathbf{A}}^{2} \mathbf{X} \mathbf{W}\right)\end{array}$

　　其中，

• • $\mathbf{W} \in \mathbb{R}^{F \times F^{\prime}}$ 为可学习参数；
  • $\sigma(\cdot)$ 为激活函数；

　　向量 $h_{i} \in \mathbb{R}^{F^{\prime}}$ 实际上总结了一个包含以节点 $v_{i}$ 为中心的二阶邻居的子图。我们将 $\mathbf{H}$ 表示为原始节点特征转换后的 自增强节点表示（ self-agumented node representations）。$\widetilde{\mathbf{X}}$ 表示低级的节点特征，它可能包含大量的噪声信息。

　　Definition 1 (Second-order Graph Regularization). 二 The objective of second-order graph regularization is to minimize the following equation

　　　　$\sum\limits_{e_{i j} \in \mathcal{E}} s_{i j}\left\|h_{i}-h_{j}\right\|_{2}^{2}$

　　其中

• • $s_{i j}$ 为二阶相似度，可定义为余弦相似度 ${\large s_{i j}=\frac{\sum\limits_{c \in \mathcal{N}(i) \cap \mathcal{N}(j)} \alpha_{i c} \cdot \alpha_{j c}}{\left\|\alpha_{i \cdot}\right\|_{2}\left\|\alpha_{j} \cdot\right\|_{2}}} $
  • $h_{i}$ 代表节点表示；　　

　　Theorem 1. Suppose that a GNN aggregates node representations as  $h_{i}^{l}=\sigma\left(\sum_{j \in \mathcal{N}(i) \cap v_{i}} \alpha_{i j} h_{j}^{l-1}\right)$ , where  $\alpha_{i j}$  stands for the element of a normalized relation matrix. If the firstorder gradient of the selected activation function  $\sigma(x)$  satisfies  $\left|\sigma^{\prime}(x)\right| \leq 1$ , then the graph neural operator approximately equals to a second-order proximity graph regularization over the node representations.

　　证明：

　　aggregation operator 为：$h^{l}=\sigma\left(\sum_{j \in \mathcal{N}(i) \cap v_{i}} \alpha_{i j} h_{j}^{l-1}\right)$

　　$\alpha_{i j}$ 为 $\tilde{\mathbf{A}}=D^{-\frac{1}{2}}(A+I) D^{-\frac{1}{2}}$ 或 $\tilde{\mathbf{A}}^{2}$ 中的元素；

　　节点表示 $h_{i}^{l}$ 可以分成三部分：

• • 自身表示：$\alpha_{i i} h_{i}^{l-1}$
  • 共同邻居表示：$\mathcal{S}_{i}= \sum\limits _{c \in \mathcal{N}(i) \cap \mathcal{N}(j)} \alpha_{i c} h_{c}^{l-1}$
  • 不同邻居表示：$\mathcal{D}_{i}=\sum\limits _{q \in \mathcal{N}(i)-\mathcal{N}(i) \cap \mathcal{N}(j)} \alpha_{i q} h_{q}^{l-1}$

　　设 $y=\sigma(x)$，并假设 所选的激活函数满足 $\left|\sigma^{\prime}(x)\right| \leq 1$，有 $\frac{\left(y_{1}-y_{2}\right)^{2}}{\left(x_{1}-x_{2}\right)^{2}}=\frac{\left|y_{1}-y_{2}\right|^{2}}{\left|x_{1}-x_{2}\right|^{2}} \leq 1$。

　　对 $h^{l}$ 重新定义为：$h^{l}=\sigma\left(\hat{h}^{l}\right)$，且 $\hat{h}^{l}=\sum_{j \in \mathcal{N}(i) \cap v_{i}} \alpha_{i j} h_{j}^{l-1}$

　　此时可得：$\left\|h_{i}^{l}-h_{j}^{l}\right\|_{2} \leq \left\|\hat{h}_{i}^{l}-\hat{h}_{j}^{l}\right\|_{2}$

　　表示 $h_{i}^{l}$ 和 $h_{j}^{l}$ 之间的距离满足：

　　　　$\begin{array}{l}\left\|h_{i}^{l}-h_{j}^{l}\right\|_{2} \leq\left\|\hat{h}_{i}^{l}-\hat{h}_{j}^{l}\right\|_{2}\\=\left\|\left(\alpha_{i i} h_{i}^{l-1}-\alpha_{j j} h_{j}^{l-1}\right)+\left(\mathcal{S}_{i}-\mathcal{S}_{j}\right)+\left(\mathcal{D}_{i}-\mathcal{D}_{j}\right)\right\|_{2}\\\leq\left\|\left(\alpha_{i i} h_{i}^{l-1}-\alpha_{j j} h_{j}^{l-1}\right)\right\|_{2}+\left\|\left(\mathcal{S}_{i}-\mathcal{S}_{j}\right)\right\|_{2}+\left\|\left(\mathcal{D}_{i}-\mathcal{D}_{j}\right)\right\|_{2}\\\leq \underbrace{\left\|\left(\alpha_{i i} h_{i}^{l-1}-\alpha_{j j} h_{j}^{l-1}\right)\right\|_{2}}_{\text {local feature smoothness }}+\underbrace{\left\|\mathcal{D}_{i}\right\|_{2}+\left\|\mathcal{D}_{j}\right\|_{2}}_{\text {non-common neighbor }}+\underbrace{\left\|\sum\limits _{c \in \mathcal{N}(i) \cap \mathcal{N}(j)}\left(\alpha_{i c}-\alpha_{j c}\right) h_{c}^{l-1}\right\|_{2}}_{\text {structure proximity }}\end{array}\quad\quad\quad(3)$　　

　　从 $Eq.3$ 可以看出，一对节点的相似度上界主要受局部特征平滑度和结构接近性的影响。根据上述证明，如果一对节点 $(v_i，v_j)$ 与许多共同的邻居相似(即 $\alpha_{i c} \approx \alpha_{j c}$) 具有平滑的局部特征和相似的结构接近性，则得到的一个 GNN 的节点表示也会使它们的节点表示更加相似。

　　整体框架：

　　

Learning from Self-augmented View

　　由于图神经层可以作为低通滤波器，其输出 $H$ 实际上是过滤掉存在于低层特征中的噪声信息后平滑的节点表示。通常，单个GNN层可能不能完美地得到一个干净的节点表示。通过多层叠加，深度GNN模型可以重复地改进前一层的表示。然而，深度GNN模型倾向于使用无限邻域混合的节点表示。在这项工作中，我们试图通过用相对平滑的节点表示来塑造低层节点特征来改进具有浅层邻域的GNN模型。

　　为了克服上述挑战，我们建议将最后一个GNN层 $\mathbf{H}$ 中学习到的知识转移到局部和全局视角下形成 $\widetilde{\mathbf{X}}$。具体地说，我们不是在同一GNN层上对节点表示 $h$ 构造对比学习损失，而是转向最大化节点表示 $h$ 与其邻域中的输入节点特征 $\widetilde{x}$ 之间的邻域预测概率。形式上，对于一个样本集 $\left\{v_{i}, v_{j}, v_{k}\right\}$，其中 $e_{i j} \in \mathcal{E}$ 但是 $e_{i k} \notin \mathcal{E}$，损失 $\ell_{j k}^{i}$ 定义为 $\left(h_{i}, \widetilde{x}_{j}\right)$ 和 $\left(h_{i}, \widetilde{x}_{k}\right)$ 的成对比较。因此，我们对GNN的自监督学习的损失函数定义如下，

　　　　$\mathcal{L}_{s s l}=\sum\limits_{e_{i j} \in \mathcal{E}} \sum\limits_{e_{i k} \notin \mathcal{E}}-\ell\left(\psi\left(h_{i}, \widetilde{x}_{j}\right), \psi\left(h_{i}, \widetilde{x}_{k}\right)\right)+\lambda \mathcal{R}(\mathcal{G})$

　　其中，$\ell(\cdot)$ 可以是一个任意的对比损失函数，$\psi$ 是一个评分函数，$\mathcal{R}$ 是一个权重为 $\lambda$ 的正则化函数，用于实现图的结构约束（将在下一节中介绍）。有很多关于对比损失 $\ell()$ 的候选者。在这项工作中，我们使用 logistic pairwise loss  $\ln \sigma\left(\psi\left(h_{i}, \widetilde{x}_{j}\right)-\psi\left(h_{i}, \widetilde{x}_{k}\right)\right)$，其中 $\sigma(x)=\frac{1}{1+\exp (-x)}$。

Self-distilling Graph Knowledge Regularization

　　在 $Eq.4$ 中定义的目标函数对输出节点表示 $h$ 和输入节点特征 $\widetilde{x}$ 之间的相互作用进行建模，这可以看作是一个从平滑的节点嵌入到去噪低级别节点特征的模型intra-model knowledge distillation 过程。然而，在边连通性上提出的对比样本可能不能代表节点表示分布的整体图景，并导致学习有利于预测边缘的节点表示的偏差。我们提出了一种如 Figure 1 所示的自馏方法，由inter-distilling modules和 intra-distilling modules 组成

Intra-distilling module

　　为了补充在单个成对样本上定义的损失，我们引入了一个正则化项，以确保在一组随机采样节点上学习节点表示 $\mathbf{H}$ 和节点特征 $\widetilde{\mathbf{X}}$ 之间关系的分布一致性。设 $L S=\left\{L S_{1}, L S_{2}, \cdots, L S_{N}\right\}$ 表示随机抽样的伪关系图，其中 $L S_{i} \subset \mathcal{V}$ 和 $\left|L S_{i}\right|=d$ 为中心节点 $v_i$ 抽样的伪局部邻居的个数。

　　计算了第 $i$ 个局部结构 $L S_{i}$ 中每个节点的估计接近度：

　　　　$\begin{aligned}S_{i j}^{t} &=\frac{\exp \left(\psi\left(h_{i}, \widetilde{x}_{j}\right)\right)}{\sum\limits_{v_{j} \in L S_{i}} \exp \left(\psi\left(h_{i}, \widetilde{x}_{j}\right)\right)} \\S_{i j}^{s} &=\frac{\exp \left(\psi\left(\widetilde{x}_{i}, \widetilde{x}_{j}\right)\right)}{\sum\limits_{v_{j} \in L S_{i}} \exp \left(\psi\left(\widetilde{x}_{i}, \widetilde{x}_{j}\right)\right)}\end{aligned}$

　　其中，$S_{i j}^{t}$ 和 $S_{i j}^{s}$ 表示节点 $v_{i}$ 和 $v_{j}$ 之间的不同节点表示估计的相似度。$S_{i j}^{t}$ 将作为教师信号，引导节点特征 $\widetilde{\mathbf{X}}=\left\{\widetilde{x}_{1}, \widetilde{x}_{2}, \cdots, \widetilde{x}_{N}\right\}$，以同意在一个随机采样图上的关系分布。对于节点 $v_{i}$ ，关系分布相似度可以测量为 $\mathcal{S}_{i}=  CrossEntropy  \left(S_{[i,] \cdot]}^{t}, S_{[i, \cdot]}^{s}\right)$。然后我们可以计算出所有节点上的关系相似度分布为

　　　　$\mathcal{R}_{\text {intra }}=\sum\limits _{i=1}^{N} \mathcal{S}_{i}$

　　其中 $\mathcal{R}_{\text {intra }}$ 作为由模型内知识生成的正则化项，并推动学习到的节点表示 $\mathbf{H}$ 和节点特征 $\widetilde{\mathbf{X}}$ 在子图级上保持一致。

Inter-distilling Module

　　该 inter-distilling module 可以通过转移学习到的自监督知识来指导目标GNN模型。通过交互蒸馏模块的多种实现，我们隐式地模拟了使用浅层GNN(例如单个GNN层)的深度平滑操作，同时避免了从高阶邻居带来的噪声信息。

　　我们通过复制目标GNN模型来创建一个教师模型 $\Phi_{t}$，然后将噪声注入到目标模型中，这些噪声在经过固定次数的迭代后将退化为一个学生模型 $\Phi_{s}$。使用自己创建的教师和学生模型 $\left\{\Phi_{t}, \Phi_{s}\right\}$，学生模型 $\Phi_{s}(\mathbf{X}, \mathbf{A})=\left\{\mathbf{H}_{s}, \widetilde{\mathbf{X}}_{s}\right\}$ 从教师模型 $\Phi_{t}$ 中提取知识。由于没有可用的标签，我们建议在图结构的约束下实现表示蒸馏。

　　知识蒸馏模块共分为两部分，定义为

　　　　$\mathcal{R}_{\text {inter }}=K D\left(\mathbf{H}_{t}, \widetilde{\mathbf{X}}_{s} \mid \mathcal{G}\right)+K D\left(\mathbf{H}_{t}, \mathbf{H}_{s} \mid \mathcal{G}\right)$

　　其中，$\mathbf{H}_{t}$ 是来自教师模型 $\Phi_{t}$ 的节点表示，和 $\widetilde{\mathbf{X}}_{s}=\mathbf{X W}$。为了定义模块 $K D(\cdot)$，我们需要满足几个要求：1)该函数应该易于计算，对反向传播策略友好；2)它应该坚持图结构约束。

　　我们利用条件随机场(CRF) 来捕获不同节点之间的成对关系。对于一般知识蒸馏模块 $K D(Y, Z \mid G)$，$Z$ 对 $Y$ 的依赖性可以根据CRF模型给出：

　　　　$P(Z \mid Y)=\frac{1}{C(Y)} \exp (-E(Z \mid Y))$

　　式中，$C(\cdot)$ 为归一化因子，$E(\cdot)$ 为能量函数，定义如下：

　　　　$\begin{aligned}E\left(Z_{i} \mid Y_{i}\right) &=\psi_{u}\left(Z_{i}, Y_{i}\right)+\psi_{p}\left(Z_{i}, Z_{j}, Y_{i}, Y_{j}\right) \\&=(1-\alpha)\left\|Z_{i}-Y_{i}\right\|_{2}^{2}+\alpha \sum\limits_{j \in \mathcal{N}(i)} \beta_{i j}\left\|Z_{i}-Z_{j}\right\|_{2}^{2}\end{aligned}$

　　其中，$\psi_{u}$ 和 $\psi_{p}$ 分别为一元能量函数和成对能量函数。参数 $\alpha \in[0,1]$ 是为了控制两个能量函数的重要性。当 $Z$ 是学生模型的节点特征，$Y$ 是教师模型 $\Phi_{m-1}$ 的节点表示时，$Eq.9$ 中定义的能量函数强制学生模型的节点 $v_i$ 表示接近于教师模型及其相邻节点。在得到能量函数后，我们可以用一个简单的分布 $Q(Z)$ 来近似分布 $P(Z|Y)$，用平均场近似的方法来解决 CRF目标。具体来说，分布 $Q(Z)$ 可以初始化为乘积边际分布为 $Q(Z)=\Pi_{i=1}^{N} Q_{i}\left(Z_{i}\right)$。通过最小化这两个分布之间的KL散度，如下：

　　　　$\arg \min K L(Q(Z) \| P(Z \mid Y))$

　　然后我们可以得到最优的 $Q_{i}^{*}\left(Z_{i}\right)$ 如下：

　　　　$\ln Q_{i}^{*}\left(Z_{i}\right)=\mathbb{E}_{j \neq i}\left[\ln P\left(Z_{j} \mid Y_{j}\right)\right]+\text { const. }$

　　根据 $Eq.8$ 和 $Eq.9$，我们可以得到

　　　　$Q_{i}^{*}\left(Z_{i}\right) \sim \exp \left((1-\alpha)\left\|Z_{i}-Y_{i}\right\|_{2}^{2}+\alpha \sum\limits_{j \in \mathcal{N}(i)} \beta_{i j}\left\|Z_{i}-Z_{j}\right\|_{2}^{2}\right)$

　　这表明 $Q_{i}^{*}\left(Z_{i}\right)$ 是一个高斯函数。通过计算其期望，我们得到了 $Z_{i}$ 的最优解如下：

　　　　$Z_{i}^{*}=\frac{(1-\alpha) Y_{i}+\alpha \sum\limits_{j \in \mathcal{N}(i)} \beta_{i j} Z_{j}}{(1-\alpha)+\alpha \sum\limits_{j \in \mathcal{N}(i)} \beta_{i j}}$

　　然后通过强制学生模型的节点表示到 $Z_{i}^{*}$ 的度量距离最小，得到 cross-model knowledge distillation 规则。将随机变量 $Y_{i}$ 替换为教师模型 $\Phi_{t}$ 的节点表示 $h_{i}^{t}$ 后，那么我们可以得到最终的蒸馏正则化如下：
　　　　$K D\left(\mathbf{H}_{t}, \widetilde{\mathbf{X}}_{s} \mid \mathcal{G}\right)=\left\|\widetilde{x}_{i}^{s}-\frac{(1-\alpha) h_{i}^{t}+\alpha \sum\limits_{j \in \mathcal{N}(i)} \beta_{i j} \widetilde{x}_{j}^{s}}{(1-\alpha)+\alpha \sum\limits_{j \in \mathcal{N}(i)} \beta_{i j}}\right\|_{2}^{2}$

　　　　$K D\left(\mathbf{H}_{t}, \mathbf{H}_{s} \mid \mathcal{G}\right)=\left\|h_{i}^{s}-\frac{(1-\alpha) h_{i}^{t}+\alpha \sum_{j \in \mathcal{N}(i)} \beta_{i j} h_{j}^{s}}{(1-\alpha)+\alpha \sum_{j \in \mathcal{N}(i)} \beta_{i j}}\right\|_{2}^{2}$

　　其中，$\widetilde{x}_{i}^{s} $ 表示学生模型 $\Phi_{s}$ 中的节点 $v_{i}$ 的特征，$h_{i}^{s}$ 表示节点 $v_{i}$ 的输出节点表示。在 $\text{Eq.13}$ 中的 $\beta_{i j}$ ，我们有很多选择，如注意权重，或平均池等。在这项工作中，我们简单地用节点表示上的平均池操作来初始化它。

　　本工作的整体自监督学习目标可以扩展如下：

　　　　$\begin{aligned}\mathcal{L}_{s s l}=\sum\limits_{e_{i j} \in \mathcal{E}} \sum\limits_{e_{i k} \notin \mathcal{E}} &-\ell\left(\psi\left(h_{i}^{s}, \widetilde{x}_{j}^{s}\right), \psi\left(h_{i}^{s}, \widetilde{x}_{k}^{s}\right)\right) \\&+\lambda\left(\mathcal{R}_{\text {intra }}+\mathcal{R}_{\text {inter }}\right)\end{aligned}$

　　其中，初始教师模型 $\Phi_{t} $ 可以通过优化所提出的自监督学习来初始化，而不需要交叉模型蒸馏正则化。

3 Experiment

数据集

　　

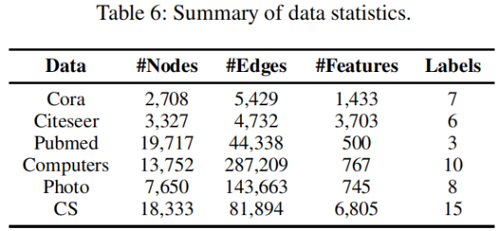
节点分类

　　

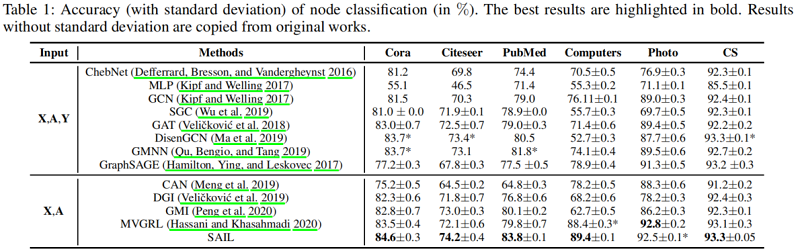
聚类

　　

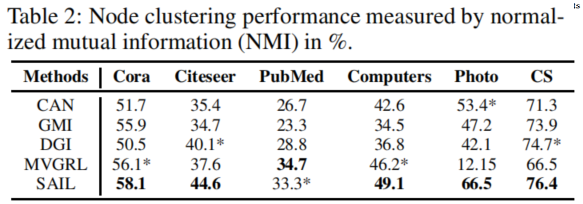
链接预测

　　

4 Conclusions

　　在这项工作中，我们提出了一种由图结构正则化的自监督学习方法(SAIL)来学习各种下游任务的无监督节点表示。我们对节点分类、节点聚类和链接预测任务进行了彻底的实验，以评估学习到的节点表示。实验结果表明，SAIL有助于学习竞争的浅层GNN，它优于用有监督或无监督目标学习的最先进的GNN。这一初步的研究可能揭示了一种很有前途的实现图神经网络自蒸馏的方法。在未来，我们计划研究如何提高该方法对对抗性攻击的鲁棒性，并学习可转移图神经网络用于下游任务，如少镜头分类。

修改历史

2022-06-22 创建文章

 

论文解读目录