论文解读（InfoGraph）《InfoGraph: Unsupervised and Semi-supervised Graph-Level Representation Learning via Mutual Information Maximization》

论文信息

论文标题：InfoGraph: Unsupervised and Semi-supervised Graph-Level Representation Learning via Mutual Information Maximization
论文作者：Fan-Yun Sun, Jordan Hoffmann, Vikas Verma, Jian Tang
论文来源：2020, ICLR
论文地址：download 
论文代码：download 

1 Introduction

 　　我们最大化了图级表示和不同尺度的子结构（如nodes、edges、 triangles）的表示之间的相互信息。

2 Method

　　我们试图通过最大化 graph-level 和 patch-level 表示之间的互信息来获得图表示。

　　局部表示和全局表示：

　　　　$h_{\phi}^{i} =\operatorname{CONCAT}\left(\left\{h_{i}^{(k)}\right\}_{k=1}^{K}\right)\quad\quad\quad(2)$

　　　　$H_{\phi}(G) =\operatorname{READOUT}\left(\left\{h_{\phi}^{i}\right\}_{i=1}^{N}\right)\quad\quad\quad(3)$

　　其中，$h_{\phi}^{i}$ 是以节点 $i$ 为中心的局部表示(patch representation)，$H_{\phi}(G)$ 是应用读出后的全局表示(global representation)。

　　本文互信息估计器（mutual information (MI) estimator）是 全局vs 局部：

　　　　$\hat{\phi}, \hat{\psi}=\underset{\phi, \psi}{\arg \max } \sum_{G \in \mathbf{G}} \frac{1}{|G|} \sum_{u \in G} I_{\phi, \psi}\left(\vec{h}_{\phi}^{u} ; H_{\phi}(G)\right)\quad\quad\quad(4)$

　　其中：

• • $|G|$ 代表图中节点数目；
  • $ I_{\phi, \psi}$ 是由鉴别器 $T_{\psi}$ 建模的互信息估计器；

　　对于上述互信息估计器，本文采用  Jensen-Shannon MI estimator 替代：

　　　　$\begin{array}{l}I_{\phi, \psi}\left(h_{\phi}^{i}(G) ; H_{\phi}(G)\right):= \\\mathbb{E}_{\mathbb{P}}\left[-\operatorname{sp}\left(-T_{\phi, \psi}\left(\vec{h}_{\phi}^{i}(x), H_{\phi}(x)\right)\right)\right]-\mathbb{E}_{\mathbb{P} \times \tilde{\mathbb{P}}}\left[\operatorname{sp}\left(T_{\phi, \psi}\left(\vec{h}_{\phi}^{i}\left(x^{\prime}\right), H_{\phi}(x)\right)\right)\right]\end{array}\quad\quad\quad(5)$

　　其中 $x$ 是一个输入样本，$x^{\prime}$ （负样本）是从 $\tilde{\mathbb{P}}=\mathbb{P}$ 采样的输入，其分布与输入空间的经验概率分布相同，$\operatorname{sp}(z)=\log \left(1+e^{z}\right)$ 是 softplus function。在实践中，我们使用一批中所有图实例的全局和局部补丁表示的所有可能组合来生成负样本。

　　由于 $H_{\phi}(G)$ 被鼓励对包含所有尺度信息局部表示进行MI计算，这有利于对跨补丁共享的数据方面和跨尺度共享的数据方面进行编码。该算法如图1所示。

　　

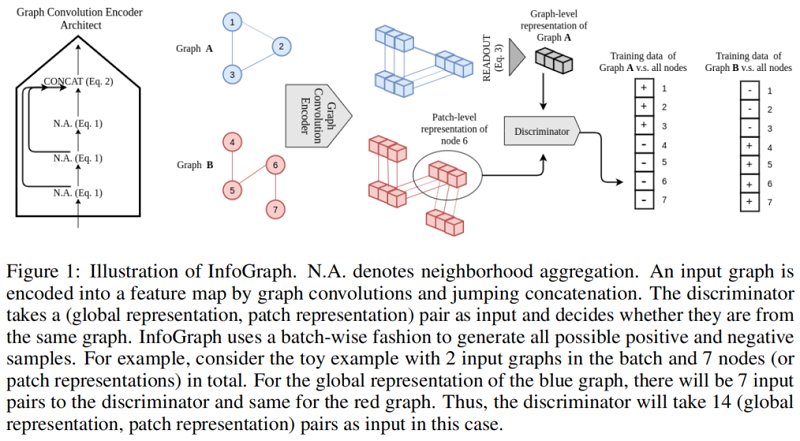
　　值得注意的是，我们的模型类似于 DGI，这是一个用于学习无监督节点嵌入的模型。然而，由于我们所关注的不同问题，存在着重要的设计差异。首先，在DGI中，他们使用随机抽样来获取负样本，因为他们主要使用专注于学习图上的节点嵌入。然而，对比方法需要大量的负样本才能竞争，因此使用批生成负样本是至关重要的，因为我们试图学习给定许多图实例的图嵌入。其次，图卷积编码器的选择也是至关重要的。我们使用GIN，而DGI使用GCN，因为GIN为图级应用提供了更好的归纳偏差。应该仔细考虑图神经网络的设计，以便图的表示可以区分其他图的实例。例如，我们使用均值求和来进行读出，这可以提供关于图形大小的重要信息。

　　图上的半监督图属性预测的损失函数：

　　　　$L_{\text {total }}=\sum\limits_{i=1}^{\left|\mathbb{G}^{L}\right|} L_{\text {supervised }}\left(y_{\phi}\left(G_{i}\right), o_{i}\right)+\lambda \sum\limits_{j=1}^{\left|\mathbb{G}^{L}\right|+\left|\mathbb{G}^{U}\right|} L_{\text {unsupervised }}\left(h_{\phi}\left(G_{j}\right) ; H_{\phi}\left(G_{j}\right)\right)$

　　其中：

• • $L_{\text {supervised }}\left(y_{\phi}\left(G_{i}\right), o_{i}\right)$ 用于度量分类器输出 $y_{\phi}\left(G_{i}\right)$ 和真实输出 $o_{i}$ 之间的差异；　　
  • $L_{\text {unsupervised }}\left(h_{\phi}\left(G_{j}\right) ; H_{\phi}\left(G_{j}\right)\right.$ 是 InfoGraph 无监督损失，如 $Eq.4$ 所示；　　

　　然而，监督任务和非监督任务可能有利于不同的信息或不同的语义空间。使用相同的编码器简单地结合这两个损失函数可能会导致 “negative transfer”。我们提出了一个简单的方法来缓解这个问题：我们部署了两个编码器模型：编码器在标记数据上的编码器（有监督编码器）和在无标记数据上的编码器（无监督编码器）。为了将学习到的表示从无监督编码器转移到有监督编码器，我们定义了一个损失项，鼓励两个编码器学习到的表示在所有表示级别上都具有高的互信息( $Eq.8$ 的第三项)。

　　　　$\begin{aligned}L_{\text {total }}=\sum\limits_{i=1}^{\left|\mathbb{G}^{L}\right|} L_{\text {supervised }}\left(y_{\phi}\left(G_{i}\right), o_{i}\right) &+\sum\limits_{j=1}^{\left|\mathbb{G}^{L}\right|+\left|\mathbb{G}^{U}\right|} L_{\text {unsupervised }}\left(h_{\varphi}\left(G_{j}\right) ; H_{\varphi}\left(G_{j}\right)\right)\quad \quad\quad(7) \\&-\lambda \sum\limits_{j=1}^{\left|\mathbb{G}^{L}\right|+\left|\mathbb{G}^{U}\right|} \frac{1}{\left|G_{j}\right|} \sum\limits_{k=1}^{K} I\left(H_{\phi}^{k}\left(G_{j}\right) ; H_{\varphi}^{k}\left(G_{j}\right) .\right. \quad \quad\quad(8)\end{aligned}$

3 Experiment

　　

　　

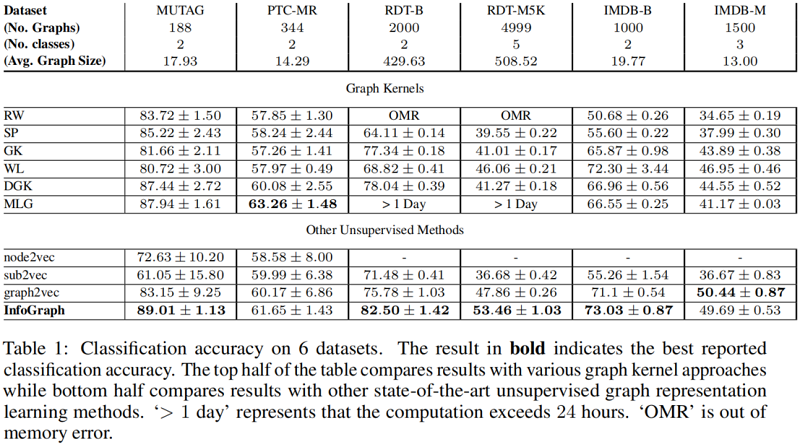
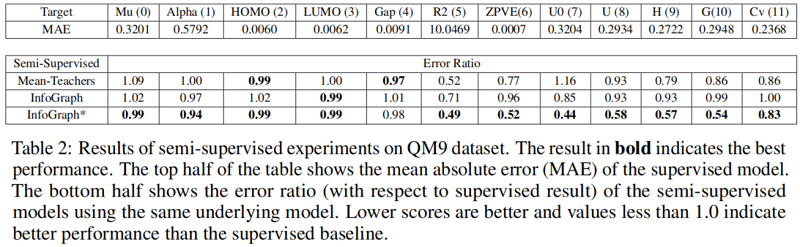
4 Conclusion

　　在本文中，我们提出了信息图来学习无监督图级表示和信息图*用于半监督学习。我们进行了图分类和分子性质预测任务的实验来评估这两种方法。实验结果表明，信息图和信息图*与现有的计算方法相比都具有很强的竞争力。关于图像数据的半监督学习的研究工作很多，但很少关注图结构数据的半监督学习。在未来，我们的目标是探索专门为图形设计的半监督框架。