论文解读(KP-GNN)《How Powerful are K-hop Message Passing Graph Neural Networks》
论文信息
论文标题:How Powerful are K-hop Message Passing Graph Neural Networks
论文作者:Jiarui Feng, Yixin Chen, Fuhai Li, Anindya Sarkar, Muhan Zhang
论文来源:NeurIPS 2022
论文地址:download
论文代码:download
1 Introduction
本文工作:
-
- 1)正式区分了 K-hop 邻居的两个不同的内核,它们在以前的工作中经常被滥用。一种是基于图扩散(graph diffusion),另一种是基于最短路径距离(shortest path distance)。我们表明,不同的 K-hop 邻居内核会导致不同的 K-hop 消息传递的表达能力;
- 2)从理论上描述了 K-hop 消息传递 GNN 的表达能力,并将所提出的定理推广到大多数现有的 K-hop 模型中;
- 3)证明了 K-hop 消息传递在严格意义上比 1-hop 消息传递更强大;
- 4)演示了无论使用哪个内核,使用 K-hop 消息传递来区分一些简单的正则图都会带来一定的限制,这促使我们进一步改进 K-hop 消息的传递;
- 5)介绍了一种新的GNN框架的k跳消息传递KP-GNN,它显著提高了标准k跳消息传递GNN的表达能力;
2 K-hop message passing and its representation power
2.1 1-hop message passing framework
经典的消息传递机制回顾:
$m_{v}^{l}=\operatorname{MES}^{l}\left(\left\{\left(h_{u}^{l-1}, e_{u v}\right) \mid u \in \mathcal{N}_{v, G}^{1}\right\}\right), h_{v}^{l}=\operatorname{UPD}^{l}\left(m_{v}^{l}, h_{v}^{l-1}\right)\quad\quad\quad(1)$
其中,$m_{v}^{L}$ 是发送到第 $l$ 层的节点 $v$ 的消息,$MESl$ 和 $UPDl$ 分别是第 $l$ 层的消息和更新函数。在 $L$ 层消息传递后,使用 $h_{v}^{L}$ 作为节点 $v$ 的最终节点表示。这种表示可用于执行节点分类和节点回归等节点级任务。要获得图表示,需要使用一个读出函数:
$h_{G}=\operatorname{READOUT}\left(\left\{h_{v}^{L} \mid v \in V\right\}\right)\quad\quad\quad(2)$
其中,读数是计算最终图表示的读出函数。然后可以使用 $h_{G}$ 来进行图分类和图回归等图级任务。
2.2 K-hop message passing framework
首先,我们区分了两个不同的 $K-hop$ 邻居核,它们在以前的研究中被互换和滥用。
shortest path distance (spd) kernel
即图 $G$ 中节点 $v$ 的第 $k$ 个跳邻居是与 $v$ 的最短路径距离为 $k$ 的节点集。
Definition 1. For a node $v$ in graph $G$ , the $K-hop$ neighbors $\mathcal{N}_{v, G}^{K, s p d}$ of $v$ based on shortest path distance kernel is the set of nodes that have the shortest path distance from node $v$ less than or equal to $K$ . We further denote $Q_{v, G}^{k, s p d}$ as the set of nodes in $G$ that are exactly the $k-th$ hop neighbors (with shortest path distance of exactly $k$ ) and $\mathcal{N}_{v, G}^{0, s p d}=Q_{v, G}^{0, s p d}=\{v\}$ is the node itself.
Definition 2. For a node $v$ in graph $G$ , the $K-hop$ neighbors $\mathcal{N}_{v, G}^{K, g d}$ of $v$ based on graph diffusion kernel is the set of nodes that can diffuse information to node $v$ within the number of random walk diffusion steps $K$ with the diffusion kernel $A$ . We further denote $Q_{v, G}^{k, g d}$ as the set of nodes in $G$ that are exactly the $k-th$ hop neighbors (nodes that can diffuse information to node $v$ with $k$ diffusion steps) and $\mathcal{N}_{v, G}^{0, g d}=Q_{v, G}^{0, g d}=\{v\}$ is the node itself.
从上述定义不难得到:
-
- 节点 $v$ 的 $K-hop$ 邻居的在两个不同的内核将是相同的,即 $\mathcal{N}_{v, G}^{K, s p d}=\mathcal{N}_{v, G}^{K, g d}$;
- 当 $K=1$ 时,$\mathcal{N}_{v, G}^{1, s p d}=Q_{v, G}^{1, s p d}=\mathcal{N}_{v, G}^{1, g d}=Q_{v, G}^{1, g d}$;
- 对于某些 $k$ $Q_{v, G}^{k, s p d}$ 并不总是等于 $Q_{v, G}^{k, g d}$ ;
- 注意,基于图扩散核,一个节点可以是 $v$ 的第 $k$ 个跳邻居;
上述两种图核的直观例子:[附上 GraphSAGE ]
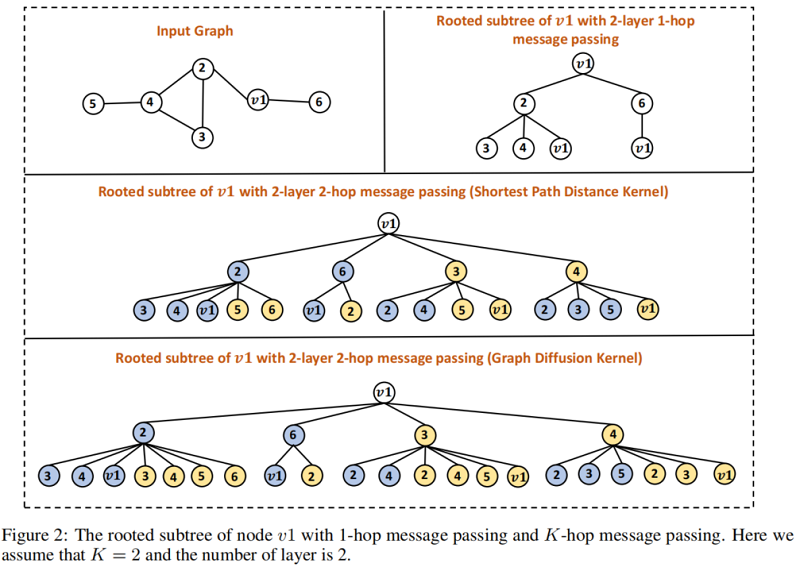
首先,如果我们执行 $1$跳消息传递,它将编码一个高 $2$ 的有根的子树,如图右上方所示。请注意,每个节点都是使用相同的参数集来学习的,这可以通过用相同的颜色(图中为白色)来表示。
现在,我们考虑使用最短路径距离内核来执行 $2$ 跳消息传递。节点 $v_1$ 的有根子树如图中间所示。我们可以看到,在每个高度,第 $1$ 跳邻居和 $2$ 跳邻居都包括在内。此外,在不同的跳中使用不同的参数集,这是通过用不同的颜色填充不同跳中的节点(蓝色表示第 $1$ 跳,黄色表示第 $2$ 跳)来表示的。
最后,在图的底部,我们展示了具有图扩散核的 $2$ 跳消息传递图神经网络。很容易看出,有根的子树不同于使用最短路径距离核的子树不同,因为节点可以同时出现在邻居的第 $1$ 跳和第 $2$ 跳中。
接下来,我们正式定义 $k-hop$ 消息传递框架如下:
$\begin{array}{l}\left.m_{v}^{l, k}=\operatorname{MES}_{k}^{l}\left(\left\{\left(h_{u}^{l-1}, e_{u v}\right) \mid u \in Q_{v, G}^{k, t}\right)\right\}\right)\\ h_{v}^{l, k}=\operatorname{UPD}_{k}^{l}\left(m_{v}^{l, k}, h_{v}^{l-1}\right)\\h_{v}^{l}=\operatorname{COMBINE}^{l}\left(\left\{h_{v}^{l, k} \mid k=1,2, \ldots, K\right\}\right)\end{array}\quad\quad\quad(3)$
其中,$t=\{s p d, g d\}$ 表示 $k$ 跳邻居的内核。在这里,对于每个跳,我们可以应用唯一的 MES 和 UPD 函数。注意,对于 $k>1$,可能不存在边特征 $e_{u v}$,因为边并不直接连接。但我们把它留在这里,因为我们可以使用另一种类型的特性来替换它。与 $Eq.1$ 中描述的 $1$ 跳消息传递框架相比,引入了组合函数来组合节点 $v$ 在不同跳下的表示。很容易看出,$L$ 层 $1-WL$ gnn实际上是 $L$ 层 $K$ 跳消息传递 GNN,如果我们只执行 $1$ 跳消息传递,我们有 $h_{v}^{l}=h_{v}^{l, 1}$。
G Implementation detail of KP-GNNCombine function1 跳消息传递 GNNs 没有 $C O M B I N E^{l}$ 功能。这里我们介绍了两种不同的 $COMBINE^{l}$ 函数。
第一个是基于注意的组合机制,它自动学习每个跳中每个节点表示的重要性。
第二种方法使用了众所周知的 geometric distribution[13]。第 $i$ 跳的的权重是基于 $\theta_{i}=\alpha(1-\alpha)^{i}$ 计算的,其中 $\alpha \in(0,1]$。最终的表示是通过所有跳的表示的加权和计算的。Peripheral subgraph information
在当前的实现中,KP-GNN只考虑外围子图中的组件数和每个组件中的边数。然而,每个节点可能有一个不同的外围子图。为了使模型能够工作,我们为实现中每个组件中的最大组件数和最大边数设置了阈值。
KP-GCN, KP-GIN, and KP-GraphSAGE
我们分别使用 GCN、GIN 和 GraphSAGE 中定义的消息和更新函数,实现了 KP-GCN、KP-GIN 和 KPGraphSAGE。
.在每个跳中,使用独立的参数集,每个跳的计算严格遵循相应的模型。但是,增加 $K$ 的数量也会增加参数的总数,这是不能扩展到 $K$。为了避免这个问题,我们采用以下方式设计了 $K-hop$ 消息传递。假设模型的总隐藏大小为H,则每个跳的隐藏大小为 $H/K$。这样,即使 $K$ 很大,模型的规模仍然在相同的尺度上。
KP-GIN+
在一个普通的 $k$ 跳消息传递框架中,将为每个节点聚合所有的 $k$ 跳邻居。这意味着,在 $L$ 层之后,GNN 的接受域为$LK$。这可能会导致训练的不稳定,因为不相关的信息可能会被聚合。为了缓解这个问题,我们采用了来自 $GINE+$[15]的想法。具体来说,我们实现了 $KP-GIN+$,它应用了与 $GINE+$ 完全相同的架构,除了在这里我们添加了外围子图信息。在第 $1$ 层,$GINE+$ 只从 $l-hop$ 内的邻居收集信息,这使得 $L$ 层 $GINE+$ 仍然有一个 $L$ 的接受域。注意,在 $KP-GIN+$ 中,我们为每个跳使用一个共享参数集。Path encoding
为了进一步利用每个跳上的图结构信息,我们引入了KP-GNN的路径编码。具体来说,我们不仅计算两个节点在跳 $k$ 处是否是邻居,而且还计算两个节点之间长度为 $k$ 的路径数。这些信息很容易计算出来,因为邻接的图 $G$ 的 $A^{k}$ 是一个长度为 $k$ 的路径计数器。然后将信息添加到AGGl中,正常的 $k$ 函数作为附加特征。Other implementation
对于所有的 GNN,我们应用 Jumping Knowledge 方法[51]来得到最终的节点表示。可能的方法包括和、平均、连接、最后一个和注意。在每一层之后都使用批处理归一化。
2.3 Expressive power of K-hop message passing framework
我们证明,当 $K>1$ 时,传递的 $K$ 跳消息严格比 $ 1-WL test$ 更强大。在整个分析过程中,我们使用正则图作为例子来说明我们的定理,因为它们不能通过 1-hop 消息传递或 $1-WL$ 测试来区分。请注意,我们的分析并不局限于正则图,但它能够描述任何图。
Definition 3. A proper $K-hop$ message passing GNN is a class of GNN models where the message, update and combine functions are all injective given the input from a countable space.
由于神经网络的 universal approximation theorem [17]和集合操作[18]的 Deep Set,很容易找到一个合适的传递 $k$ 跳消息的 GNN。在后面的部分中,默认情况下,所有提到的传递 GNN 的 $k$ 跳消息都是正确的。接下来,我们定义节点配置。
Definition 4. The node configuration of node $v$ in graph $G$ within $k$ hops under $t$ kernel is a list $A_{v, G}^{k, t}=\left(a_{v, G}^{1, t}, a_{v, G}^{2, t}, \ldots, a_{v, G}^{k, t}\right)$ , where $a_{v, G}^{i, t}=\left|Q_{v, G}^{i, t}\right|$ is the number of $i$-th hop neighbors of node $v$ .
当我们说两个节点构型 $A_{v_{1}, G^{(1)}}^{k, t}$ 和 $A_{v_{2}, G^{(2)}}^{k, t}$ 相等时,我们的意思是这两个列表在组件上是相等的。现在我们可以提出第一个命题:
Proposition 1. For two graphs $G^{(1)}=\left(V^{(1)}, E^{(1)}\right)$ and $G^{(2)}=\left(V^{(2)}, E^{(2)}\right)$ , we pick two nodes $v_{1}$ and $v_{2}$ from two graphs respectively. Given a proper $1$-layer $K$-hop message passing GNN, it can distinguish $v_{1}$ and $v_{2}$ if $A_{v_{1}, G^{(1)}}^{K, t} \neq A_{v_{2}, G^{(2)}}^{K,}$ .
Proposition 1 证明
上述证明主要利用:
- 对于每一跳的参数不同;
- $\left|Q_{v, G}^{k, t}\right|$ 在特定的 $k$ 不同,且结合 GNN 单射性质;
首先说明 Corollary 1 为什么正确?
当 $K=1$ 时,$v_1$ 和 $v_2$ 的节点构型为 $d_{v_{1}, G^{(1)}}$ 和 $d_{v_{2}, G^{(2)}}$,其中 $d_{v, G}$ 为 $v$ 的节点度。在 $L$ 个层之后,GNN 可以得到 $L$ 个跳数内每个节点的节点配置。根据这句话,可以很容易地看出为什么这些 GNN 不能区分任何 大小为 $n$ 的 $\text{r-regular graph}$,因为正则图中的每个节点都具有相同的度。从另一个角度来看,1 跳消息传递GNN的表达能力是有限的,因为它只有GNN接受域内图中每个节点的度信息。
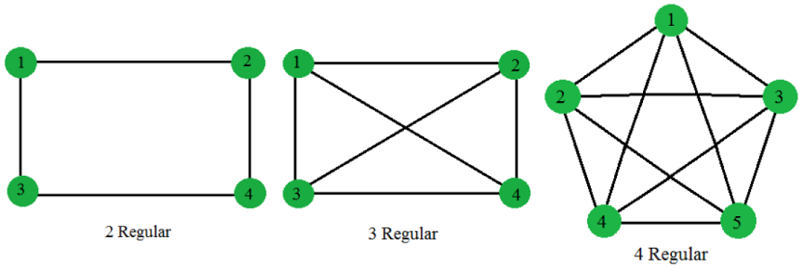
知识点:正则图
正则图是指各顶点的度均相同的无向简单图。
在图论中,正则图中每个顶点具有相同数量的邻点; 即每个顶点具有相同的度或价态。 正则的有向图也必须满足更多的条件,即每个顶点的内外自由度都要彼此相等。具有 $k$ 个自由度的顶点的正则图被称为 $k$ 度的 $k$-正则图。 此外,奇数程度的正则图形将包含偶数个顶点。例子:
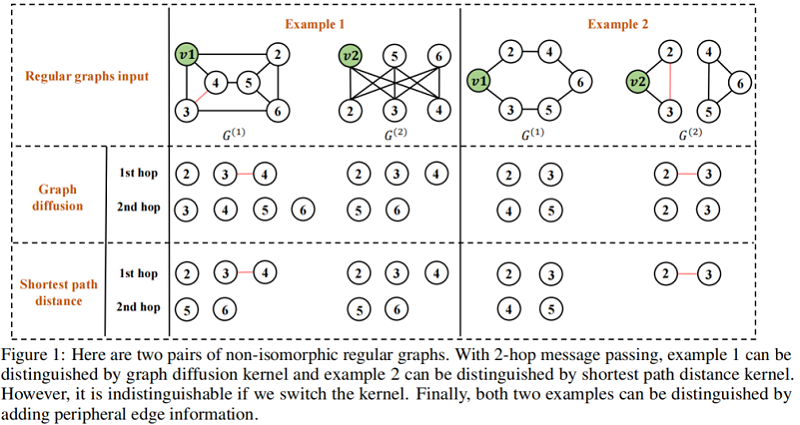
当 $K>1$ 时,$K$ 跳消息传递至少与 $1$ 跳消息传递同等强大,因为K跳消息传递包含了$1$ 跳消息传递所具有的所有信息。为了了解为什么它更强大,我们使用了两个例子来说明它。第一个示例显示在图1的左侧部分。假设我们使用图扩散核,我们想学习节点的表示 $v_1$ 和节点 $v_2$ 两个图,我们知道 $1$ 跳消息传递框架产生相同的表示两个节点都是大小为 $6$ 的 $3$ 正则图。但是,很容易看出 $v_1$ 和 $v_2$ 有不同的局部结构,应该有不同的表示。相反,如果我们使用与图扩散核一起进行的两跳消息传递,我们可以通过检查节点的第二跳邻居来很容易地区分这两个节点,因为节点 $v_1$ 有四个第二跳邻居,而节点 $v_2$ 只有两个第二跳邻居。第二个示例如图1的右侧所示。本例中的两个图仍然是规则图,$1$ 跳消息传递仍然无法区分节点 $v_1$ 和节点 $v_2$。相比之下,假设我们使用最短路径距离核,节点 $v_1$ 和 $v_2$ 有不同数量的第 $2$ 跳邻居,因此通过执行 $2$ 跳消息传递将有不同的表示。这两个例子令人信服地证明了用 $K>1$ 传递的 $K$ 跳消息比 $K=1$ 具有更好的表达能力。
接下来,我们简要总结了一些现有的传递 $k$ 跳消息的 GNN,它们的表达能力可以用 Proposition1 来描述。Corollary 2. When $K>1$ and $t=spd$ , Proposition 1 characterizes the expressive power of GINE [15]]. It also characterize DEA-GNN [19] and Graphormer [20] with shortest path distance as the distance feature or the spatial encoding respectively.
此外,我们提出的 $K-hop$ 消息传递框架比之前的一些基于图扩散的 $GNNs$,如 MixHop[11],GPR-GNN[14],magna[13]更强大。我们将详细的讨论留在附录C中
2.4 Limitation of K-hop message passing framework
请继续查看所提供的示例。在 example 1中,我们知道节点 $v_1$ 和 $v_2$ 与图扩散核有不同数量的第二跳邻居。但是,如果我们使用最短路径距离核,则这两个节点在第 2 跳中有相同数量的邻居,这意味着我们不能使用具有最短路径距离核的 2 跳消息传递来区分两个节点。类似地,在 example 2 中,两个节点在具有图扩散核的第 1 跳和第 2 跳中具有相同数量的邻居。这些结果突出表明,内核的选择会影响 $k$ 跳消息传递的表达能力。此外,它们都不能通过 2 跳消息传递来区分这两个示例。鉴于所有这些观察结果,我们可能会想知道是否有一种方法可以进一步提高 $k$ 跳消息传递的表达能力?
3 KP-GNN: improving the power of K-hop message passing by peripheral subgraph
3.1 Peripheral edge and peripheral subgraph
Definition 5. The peripheral edges $E\left(Q_{v, G}^{k, t}\right)$ are defined as the set of edges that connect nodes within set $Q_{v, G}^{k, t}$ . We further denote $\left|E\left(Q_{v, G}^{k, t}\right)\right|$ as the number of peripheral edges. The peripheral subgraph $G_{v, G}^{k, t}=\left(Q_{v, G}^{k, t}, E\left(Q_{v, G}^{k, t}\right)\right)$ is defined as the subgraph induced by $Q_{v, G}^{k, t}$ from the whole graph $G$ .
3.2 K-hop peripheral-subgraph-enhanced graph neural network
KP-GNN 消息传递函数如下:
$\hat{h}_{v}^{l, k}=\operatorname{MES}_{k}^{l}\left(\left\{\left\{\left(h_{u}^{l-1}, e_{u v}\right) \mid u \in Q_{v, G}^{k, t}\right\}, G_{v, G}^{k, t}\right)\right.\quad\quad\quad(4)$
在第 $k$ 跳的消息步骤中,我们不仅聚合了邻居的信息,而且还聚合了第 $k$ 跳的外围子图。KP-GNN的实现可以非常灵活,因为任何图编码函数都可以使用。为了最大化模型可以在保持简单的同时编码的信息,我们实现了消息函数为:
${\large \operatorname{MES}_{k}^{l}=\operatorname{MES}_{k}^{l, \text { normal }}\left(\left\{\left(h_{u}^{l-1}, e_{u v}\right) \mid u \in Q_{v, G}^{k, t}\right\}\right)+\sum \limits_{c \in C} \frac{1}{|C|} \sum \limits_{(i, j) \in E\left(Q_{v, G}^{k, t}\right)_{c}} e_{i j}} \quad\quad\quad(5)$
其中
-
- $\operatorname{MES}_{k}^{l, \text { normal }}$ 表示原始GNN模型中的消息函数;
- $C$ 是 $G_{v, G}^{k, t}$ 中连接组件的集合;
- $E\left(Q_{v, G}^{k, t}\right)_{c}$ 是 $G_{v, G}^{k, t}$中第 $c$ 个连接分量的边集;
这种实现有助于KP-GNN不仅编码 $E\left(Q_{v, G}^{k, t}\right)$,还可以编码 $G_{v, G}^{k, t}$(组件数量)的部分信息。有了这个实现,任何GNN模型都可以被合并到KP-GNN框架中并得到增强,通过用每个跳 $k$ 的相应函数替换 $\mathrm{MES}_{k}^{l, \text { normal }}$、正常 $k$ 和 $\mathrm{UPD}_{k}^{l}$。我们在附录G中留下了详细的实现。
3.3 The expressive power of KP-GNN
在本节中,我们从理论上描述了KP-GNN的表达能力,并将其与原始的K-hop消息传递框架进行了比较。关键的观点是,根据 $\text{Eq.4}$,与正常的 $k$ 跳消息传递相比,第 $k$ 跳的消息函数另外编码了 $G_{v, G}^{k, t}$。然后,我们提出以下定理。
Theorem 1. For two graphs $G^{(1)}=\left(V^{(1)}, E^{(1)}\right)$ and $G^{(2)}=\left(V^{(2)}, E^{(2)}\right)$ , we pick two nodes $v_{1}$ and $v_{2}$ from two graphs respectively. Suppose there is a proper $K-hop$ $1$-layer KP-GNN with message functions as powerful as $w$-WL test on distinguishing graph structures. Then it can distinguish $v_{1}$ and $v_{2}$ if $G_{v_{1}, G^{(1)}}^{k, t}$ and $G_{v_{2}, G^{(2)}}^{k, t}$ are non-isomorphic and $w$-WL test distinguishable for some $k \leq K$ .
Theorem 2. Consider all pair of $n$-sized $r$-regular graphs, where $3 \leq r<\sqrt{2 \log n}$ . For any small constant $\epsilon>0$ , there exists a KP-GNN using shortest path distance as kernel and only peripheral edge information with at most $K=\left\lceil\left(\frac{1}{2}+\epsilon \frac{\operatorname{logn}}{\log (r-1-\epsilon)}\right)\right\rceil$ , which distinguishes almost all $(1-o(1))$ such pair of graphs with only $1$-layer message passing.
上述定理证明了仅利用 peripheral edge 信息的 KP-GNN 的简单实现可以区分几乎所有具有一定 $K$ 层和 $1$ 层的正则图。
此外,根据 Distance Encoding [19] 中的定理3.7,具有最短路径距离核的 $k$ 跳消息不能区分任何具有相同交集数组的任何距离正则图。这里我们证明了 $KP-GNN$ 在区分距离正则图方面比距离编码更强大。
Theorem 3. For two non-isomorphic distance regular graphs $G^{(1)}=\left(V^{(1)}, E^{(1)}\right)$ and $G^{(2)}= \left(V^{(2)}, E^{(2)}\right)$ with the same intersection array $\left(b_{0}, b_{1}, \ldots, b_{d-1} ; c_{1}, c_{2}, \ldots, c_{d}\right)$ , we pick two nodes $v_{1}$ and $v_{2}$ from two graphs respectively. Given a proper $1$-layer $K$-hop KP-GNN with message functions defined in Equation (5), it can distinguish $v_{1}$ and $v_{2}$ if $b_{0}-b_{j}-c_{j}=2$ for some $j \leq K$ and $G_{v_{1}, G^{(1)}}^{j, t}$ and $G_{v_{2}, G^{(2)}}^{j, t}$ are non-isomorphic.
4 Experiments
4.1 Datasets
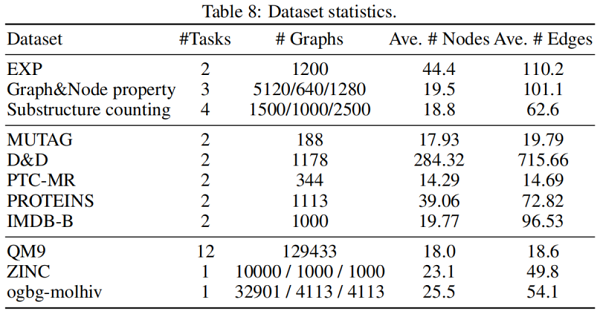
4.2 Empirical verification of the expressive power
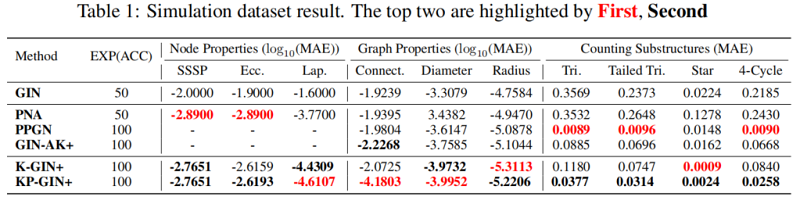
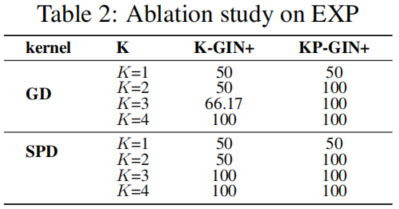
4.3 Evaluation on TU datasets
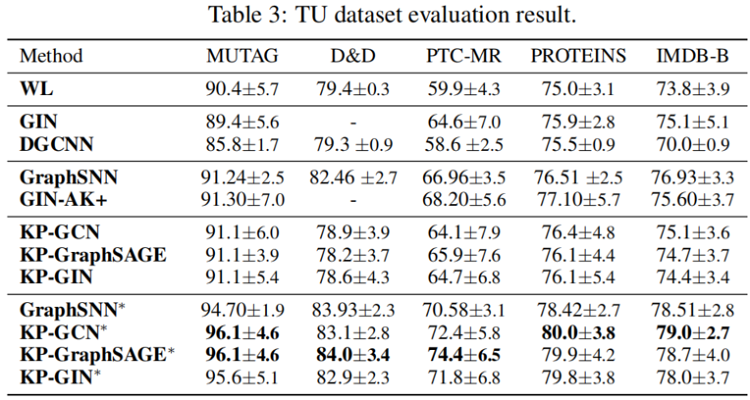
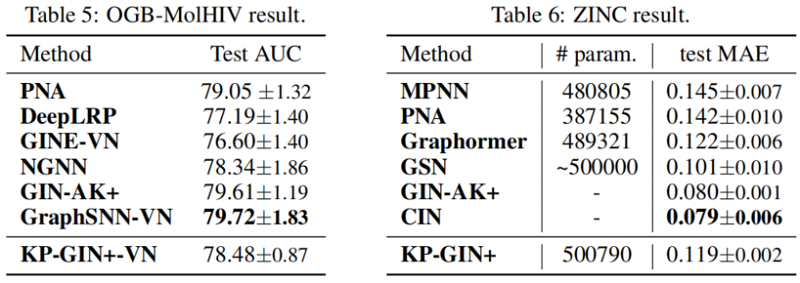
4.4 Evaluation on molecular prediction tasks
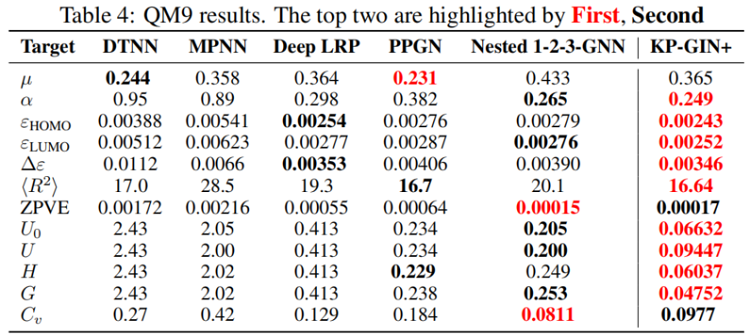
5 Conclusion
修改历史
2022-06-20 创建文章
因上求缘,果上努力~~~~ 作者:图神经网络,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/16390878.html