论文解读（GLNNs）《Graph-Less Neural Networks: Teaching Old MLPs New Tricks Via Distillation》

论文信息

论文标题：Graph-less Neural Networks: Teaching Old MLPs New Tricks via Distillation
论文作者：Shichang Zhang, Yozen Liu, Yizhou Sun, Neil Shah
论文来源：2022, ICLR
论文地址：download 
论文代码：download 

1 Introduction

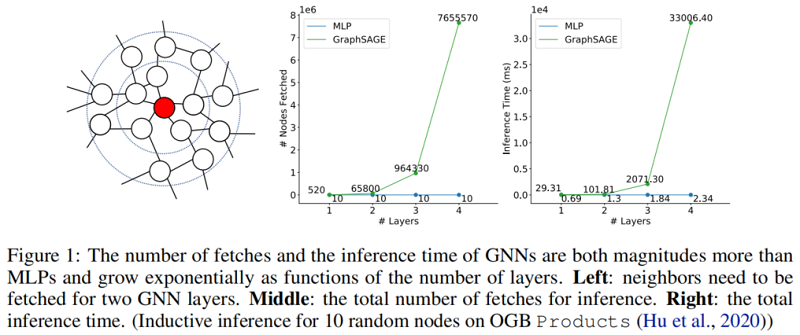
　　GNN 在图上受领域聚合的限制，经典的加速方法如 pruning 和 quantization，可以减少乘法和累积的操作（MAC）。MLP 并不存在上述图依赖的问题，反倒是避免了关系数据之间常存在的冷启动问题的辅助好处，即使遇到新的节点邻居信息不能立刻使用，MLP也可以合理推断。

　　Figure 1 显示了每个 GNN 层所添加的依赖性和推理时间的指数爆炸：

　　

2 Method

　　下文将考虑这 6 个问题：

• 1) How do GLNNs compare to MLPs and GNNs?
• 2) Can GLNNs work well under both transductive and inductive settings?
• 3) How do GLNNs compare to other inference acceleration methods?
• 4) How do GLNNs benefit from KD?
• 5) Do GLNNs have sufficient model expressiveness?
• 6) When will GLNNs fail to work?

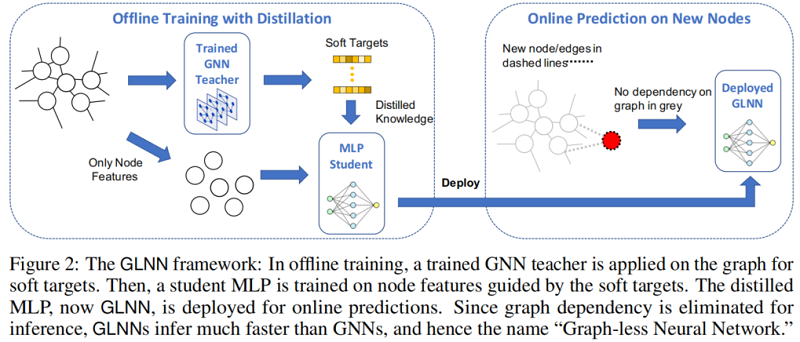
2.1 Framework

　　简而言之，我们通过 KD 从 teacher  GNN 那里训练了一个“增强”的MLP。在我们的例子中，我们使用一个 teacher  GNN 为每个节点 $v$ 生成软目标 $\boldsymbol{z}_{v}$。然后，我们训练一个同时具有真实标签 $\boldsymbol{y}_{v}$ 和 $\boldsymbol{z}_{v}$ 的 student MLP。目标是 $Eq.1$，$\lambda$ 是一个权值参数，$\mathcal{L}_{\text {label }}$ 是 $\boldsymbol{y}_{v}$ 和学生预测 $\hat{\boldsymbol{y}}_{v}$ 之间的交叉熵，$\mathcal{L}_{\text {teacher }}$ 是 kl 散度。

　　　　$\mathcal{L}=\lambda \Sigma_{v \in \mathcal{V}^{L}} \mathcal{L}_{l a b e l}\left(\hat{\boldsymbol{y}}_{v}, \boldsymbol{y}_{v}\right)+(1-\lambda) \Sigma_{v \in \mathcal{V}} \mathcal{L}_{\text {teacher }}\left(\hat{\boldsymbol{y}}_{v}, \boldsymbol{z}_{v}\right)$

　　KD之后的模型，即 GLNN，本质上是一个 MLP。因此，GLNN 在推理过程中没有图的依赖性，其速度与 MLP 一样快。另一方面，通过  offline KD ，GLNN参数被优化，以预测和泛化以及 GNN，具有更快的推理和更容易部署的额外好处。在 Figure 2 中，我们展示了GLNN 的 offline K 和在线推理步骤。

　　

3 Experiment

3.1 Datasets

　　

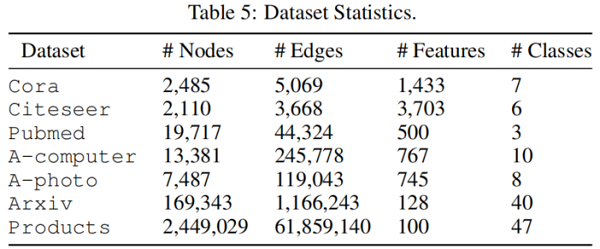
3.2 Model Architectures

　　Teacher GNN：GraphSAGE、GCN、GAT、APPNP

3.3 Evaluation Protocol

　　10 次标准训练获得统计特征。实验报告 test accuracy，val datasets 用于选择最佳模型。

3.4 Transductive vs. Inductive

　　图 $\mathcal{G}$ 和相应节点特征和标签 $\mathbf{X}$, $\mathbf{Y}^{L}$，节点分类目标有两个分别是直推式任务 transductive (tran) 和归纳式任务 inductive (ind)。

　　为进行试验，首先选择节点集 $\mathcal{V}_{i n d}^{U} \subset \mathcal{V}^{U}$ ，其中 $\mathcal{V}^{U}=\mathcal{V}_{o b s}^{U} \cup \mathcal{V}_{i n d}^{U}$。所有的边都连接到 $\mathcal{V}_{\text {ind }}^{U}$ 中的节点。因此最终得到两个不相交的图 $\mathcal{G}=\mathcal{G}_{\text {obs }} \cup \mathcal{G}_{\text {ind }}$，具有共享节点或边。节点 特征和标签被划分为三个不相交的集合 $\mathbf{X}=\mathbf{X}^{L} \cup \mathbf{X}_{o b s}^{U} \cup \mathbf{X}_{i n d}^{U}$, $\mathbf{Y}=\mathbf{Y}^{L} \cup \mathbf{Y}_{o b s}^{U} \cup \mathbf{Y}_{i n d}^{U}$

• tran: 在 $\mathcal{G}$, $\mathbf{X}$, $\mathbf{Y}^{L}$ 进行训练，在 $\left(\mathbf{X}^{U}, \mathbf{Y}^{U}\right)$ 上进行验证，KD 使用 $z_{v}, v \in \mathcal{V}$；
• ind: 在 $\mathcal{G}_{o b s}$, $\mathbf{X}^{L}$, $\mathbf{X}_{o b s}^{U}$, $\mathbf{Y}^{L}$ 进行训练，在 $\left(\mathbf{X}_{i n d}^{U}, \mathbf{Y}_{i n d}^{U}\right)$ 上进行验证， KD 使用 $z_{v}, v \in \mathcal{V}^{L} \cup \mathcal{V}_{o b s}^{U} $

3.5 How do GLNNs compare to MLPs and GNNs

　　首先考虑标准的 transductive 设置，所以我们的结果在 Table 1 中：

　　

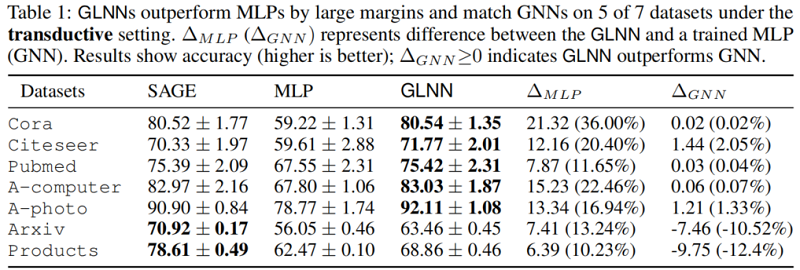
　　如 Table 1 所示，所有 GLNN 的性能都比 MLP 大幅提高。在较小的数据集（前5行）上，GLNN 甚至可以优于教师的 GNN。

　　对于较大的OGB数据集（最后2行），GLNN的性能比 MLP 有提高，但仍然比教师的 GNN 更差。然而，如 Table 2 所示，这一差距可以通过增加 MLP 大小到 $MLP_{wi}$ 来缓解。$w_i$ 用于表示隐藏层被放大了 $i$ 倍，例如 $MLP_{w_4}$ 的隐藏层比上下文中给出的 MLP 宽 4 倍。

　　

3.6 Can GLNNs work well under both transductive and inductive settings

　　

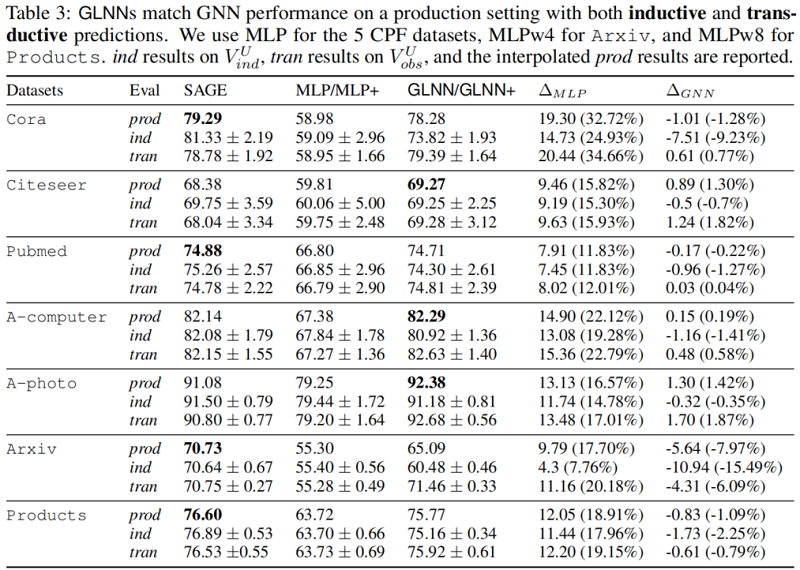
　　为了对模型进行归纳评估，形成一个归纳子集，即  $\mathcal{V}^{U}=\mathcal{V}_{o b s}^{U} \cup \mathcal{V}_{i n d}^{U}$  。在实际应用中，模型 可能会在时间上周期性地进行再训练。  $\mathcal{V}_{i n d}^{U}$  中的滞留节点表示两次训练之间进入的新节点。在实验中，为了减少随机性和评估泛化性，作者考虑一个更大的  $\mathcal{V}_{i n d}^{U}$ ，其中包含  $20\%$  的测试数 据。此外还评估了包含其他  $80\%$  测试数据的  $\mathcal{V}_{o b s}^{U}$  ，表示对现有末标记节点的标准直推式预测， 因为在现实情况下，推理过程通常是基于现有的节点重新进行的。

3.7 How do GLNNs compare to other inference acceleration methods

　　

　　QSAGE (FP32 -> INT8)，PSAGE（50% weights pruned），Neighbor sample 的设置可见图 1。

　　另外两种被认为是推理过程加速的方法是 GNN-to-GNN KD，如 TinyGNN 和 GA-MLPs，如 SGC 或 SIGN。GNN-to-GNN KD 的推理过程可能比与学生相同 i 的 GNN-Li 慢，因为通常会有一些额外模块引入的开销。GA-MLPs 预先计算增强节点特性，并应用 MLPs 。通过预计算，它们的推理时间与 SGC 的 MLPs 相同，与涉及拼接的增强 (SIGN) 的放大 MLPwi 相同。因此，对于这两种方法，比较 GLNN 中 GNN-Li 和 MLPwi 就足够了。

　　

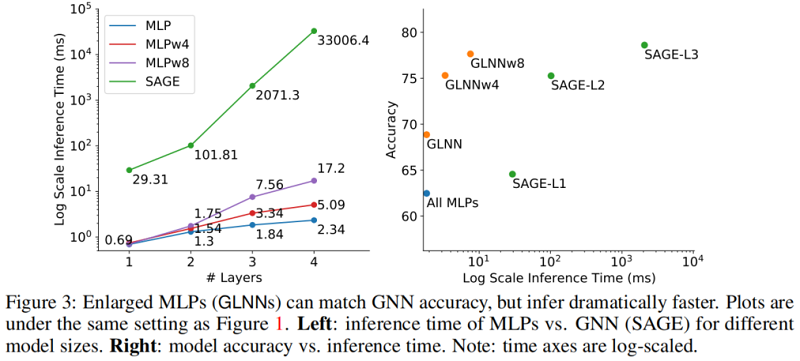
　　GNN-Lis 比 MLPs 慢得多。对于 GA-MLPs，由于不能对归纳节点进行完整的预计算，GA-MLPs 仍然需要获取邻居节点。这使得它们在归纳设置中比 MLPwi 要慢得多，甚至比剪枝 GNN 和 TinyGNN 还要慢。

3.8 How does GLNNs benefit from KD

　　作者发现 GNN 在节点分类任务上明显优于 MLPs。但是如果加入 KD, GLNN 往往可以与 GNN 相竞争。这表明如果存在合适的 MLP 参数，可以很好地逼近从节点特征到标签的理想预测函数。然而，这些参数很难通过标准的随机梯度下降法学习。因此假设 KD 通过诱导偏差的正则化和转换来帮助发现最佳参数。

　　首先证明 KD 可以帮助规范 Student MLP 和防止过拟合。图 4 中直接训练 MLP 和 GLNN 的损失曲线，MLP 的训练损失和验证损失的差距明显大于 GLNN, MLPs 表现出明显的过拟合趋势。

　　

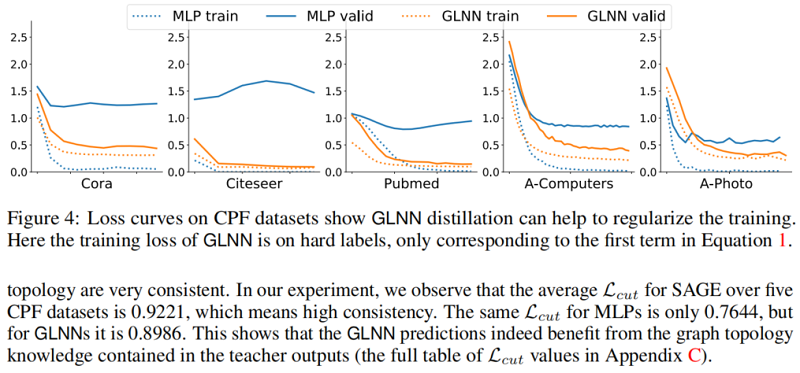
　　其次分析使 GNN 具有强大的节点分类能力的归纳偏差，表明节点类别的推理过程应该受到图拓扑 的影响，尤其是邻居节点的影响。作者假设 KD 有助于降低诱导偏差，因此 GLNN 可以表现出竞 争力。由于归纳偏差，Teacher GNN 的软标签受图拓扑的影响很大。为了定量分析 Teacher GNN 软标签分布对 Student MLP 训练过程的影响，作者定义 cut loss $\mathcal{L}_{\text {cut }} \in[0,1]$ 来量化模 型预测与图拓扑之间的一致性:

　　　　$\mathcal{L}_{c u t}=\frac{\operatorname{Tr}\left(\hat{\mathbf{Y}}^{T} \mathbf{A} \hat{\mathbf{Y}}\right)}{\operatorname{Tr}\left(\hat{\mathbf{Y}}^{T} \mathbf{D} \hat{\mathbf{Y}}\right)}$

　　其中 $\hat{\mathbf{Y}} \in[0,1]^{N \times K}$ 代表模型输出的软标签分布概率， $\mathbf{A}, \mathbf{D}$ 分别代表邻接矩阵和度矩阵。 当 $\mathcal{L}_{c u t}$ 接近 $1$ 时，表示预测结果与图拓扑非常一致。在实验中观察到 SAGE 在 5 个 CPF 数据 集上的平均 $\mathcal{L}_{c u t}$ 为 $0.9221$ ，这意味着高一致性。MLPs 的相同 $\mathcal{L}_{\text {cut }}$ 仅为 0.7644，而 GLNN 为 0.8986。这说明 GLNN 预测确实受益于教师输出中包含的图拓扑知识。

修改历史

2022-06-18 创建文章

论文解读目录

 

GNN 加速的论文：

Accelerating large scale real-time GNN inference using channel pruning——2021

Degree-quant: Quantization-aware training for graph neural networks——2021

Learned low precision graph neural networks——2020